《简单的排列》教学设计

陈李勇

【教学内容】

人教版二年级上册第97页。

【教学过程】

一、开门见山，展开新课

1.解读信息，提出疑问。

谈话：学数学就要与数字打交道。今天智慧爷爷给大家带来了一道题，想考考大家。你们有信心迎接挑战吗？

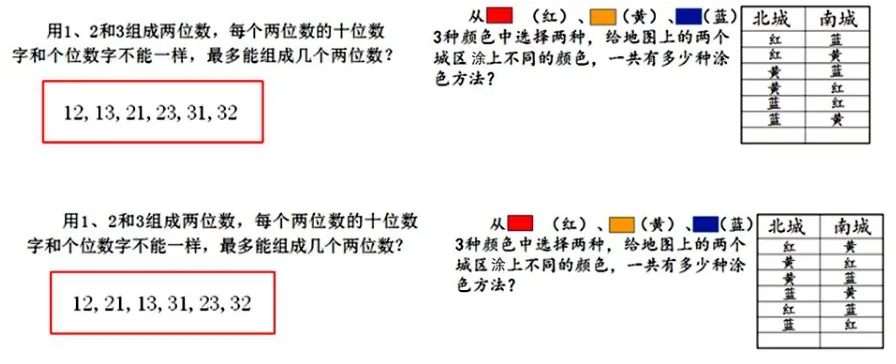
课件出示：用1、2和3组成两位数，每个两位数的十位数和个位数不能一样，最多能组成几个两位数？

谈话：有什么不明白的地方吗？

学生自由提问，教师和其他同学帮忙解疑。重点强调：两位数、十位数和个位数不同（排除11、22等错误），“最多”就是要写全但不能重复。

【设计意图：有效的学习活动必须建立在明确的规则之上。在学生自主活动前让学生针对这一问题提出疑惑之处，是为了保证其在随后的自主探究活动中更好地理解，提高课堂有效性。值得说明的是，笔者根据第一次执教的结果，加上了“最多”二字，使题目要求表述更规范。】

2.自主探究，学习新知。

谈话：请大家用1、2、3三张数字卡片，先摆一摆，再写一写，完成后与同桌交流。

3.交流反馈。

谈话：写出一个的请举手。写出两个的请举手……写出比6个多的请举手。（写出6个的占绝大多数）

作品（1）：12,13,21,23,31,32

作品（2）：12,21,13,31,23,32

学生代表上台解读，教师把这两种方法板书在黑板上。

交流：第一种方法有什么特点？第二种呢？如果请你给这两种方法各取一个名字，你会怎么取呢？

学生自由发表意见，最后形成统一：固定十位法、交换法。

完善：有固定十位法，那么肯定有——？

生：固定个位法。

师：你们很会思考。请你在纸上试着用“固定个位法”写一写。

4.对比优化。

追问：刚才有同学写出的不是6个，究竟是怎么回事呢？我们一起看看。

投影呈现遗漏和重复的作品。让学生围绕这些作品出现的问题展开交流。

预设（1）：太乱了，漏了一个。教师板书：遗漏。

预设（2）：重复了一个。教师板书：重复。

设疑：这些作品不是遗漏了几个就是重复了几个。那么，怎么就能不重复、不遗漏呢？

预设（1）：固定十位法和交换法是有规律的。

预设（2）：刚才的方法都是有顺序的。

小结：大家说法不同，但道理一样。只有按照一定的规律和顺序去写，才能做到不重复、不遗漏。

顺势让学生再次回顾用固定法和交换法解决问题的过程，体会其优越性。

5.强化方法。

谈话：“固定法”和“交换法”都是很好的方法。刚才用“固定十位法”的同学，请再用“交换法”写一写；刚才用“交换法”的同学，请再用“固定法”写一写。

【设计意图：先反馈正确的作品，再反馈有瑕疵的作品，让学生经历一个优化的过程，使他们对排列方法的理解与感悟更加深刻。本环节的多个活动，比如给方法命名，用刚才没用过的方法再写一写等，均能起到巩固作用。】

二、拓展延伸，初步建模

1.涂色问题。

谈话：解决了数字的搭配问题，我们再来解决一个涂色的问题。

课件出示：

反馈。学生代表上台展示，每次都让其他学生先观察并判断采用的是“固定法”还是“交换法”。

作品一：

作品二：

学生均能快速作出判断。

作品三：

学生难以判断。教师追问：为什么你们判断的速度明显比前两次慢了？（杂乱无章且存在错误）继续出示。

作品四：

作品五：

2.比较交流，优化方法。

提问：你有什么发现？

生：第三个有错误，不同的城区要用不同的颜色，第四个有遗漏，第五个有重复。

生：我还发现虽然题目中有7格，但是我们不用全涂满。

师：解决搭配问题的关键就是做到不重复、不遗漏，那么怎样才能做到不重复、不遗漏呢？

（要有序思考，采用交换法或者固定法）

随后用课件再演示一次，以帮助学生加深理解。

3.初建模型。

谈话：刚才我们解决了数字的排列问题和城区的涂色问题，现在回过头来看看，这两个问题有没有什么联系呢？

预设（1）：结果都是6个。

预设（2）：都可以用固定法和交换法解决。

预设（3）：我发现北城和南城就相当于第一个问题的“十位”和“个位”。

预设（4）：我还发现三种颜色就相当于数字1、2、3。

至此，学生已完成初步建模。

【设计意图：涂色问题和数字的搭配问题看似相差很远，实则是同一模型下的不同体现。在两个看似缺乏共性的素材之间发现它们的相同点，十分有利于模型的构建。】

三、多样练习，进一步建模

1.递进练习。

（1）小明有如下的三种硬币各一枚。现在他想选择其中的两枚，分别放在左手和右手里。他一共有多少种方法？

引导学生发现：三枚硬币就相当于数字1、2、3，两只手就相当于十位、个位。

（2）丽丽、军军、红红三人一起照相。

①三人合影一共可以有多少种不同的排法？

②如果军军一定要站在中间，可以照多少张不同的照片呢？

（3）从甲地到乙地有两条路，从乙地到丙地有三条路，那么，从甲地经过乙地再到丙地一共有多少种走法？

引导学生明白可以把路线分别标记为a、b、1、2、3，达到简化的目的，从而渗透符号意识。

2.抽象建模。

师：现在你对搭配问题有什么了解？

生：情境变了，但问题的本质不变。

生：解决的方法没变。

【设计意图：让学生体会到“变与不变”是模型思想的最大特征。变的是情境，不变的是本质、方法。】

四、课堂总结，升华认知