“运算能力”素养取向的复习课设计——以《小数加减法》整理与复习为例

方巧娟

【教学内容】

人教版四年级《小数加减法》。

【教学过程】

一、问题解决，生成复习材料

1．创设情境，解读信息，提出数学问题。

师：同学们，今天老师带了一个与小数有关的问题。你能找到哪些数学信息？

生：小明带了50元钱，①号笔记本12.4元，②号笔记本6.62元，③号笔记本7.6元。

师：你能根据这些数学信息提出数学问题吗？

生：①号笔记本和②号笔记本一共要多少元？

生：三本笔记本一共要几元？

师：看来，同学们都能提出与小数有关的数学问题。请把你的数学问题记录在《作业单》上，并列出算式，不计算。

2．学生独立在《作业单》上记录自己提出的问题，并列出算式。

3．交流反馈，呈现典型算式。

教师巡视，收集学生代表性作品，组织汇报交流，互动反馈。

反馈方式一：学生汇报自己的数学问题，然后介绍相应算式。

生：我提的问题是：①号笔记本和②号笔记本一共要多少元？算式是12.4+6.62。

生：我提的问题是三本书一共要多少元？算式是12.4+6.62+7.6。

反馈方式二：学生出示算式，请其他同学猜提了什么数学问题。

生：我的算式是7.6-6.62，大家猜猜我提的是什么问题？

生：你的问题是“③号笔记本比②号笔记本贵几元？”。

生：我的算式是50-12.4，大家猜猜我提的是什么问题？

生：你的问题是“50元钱买了①号笔记本能找回几元？”。

反馈方式三：教师补充算式，请学生猜提了什么数学问题。

师：方老师也列了一个算式，50-12.4-7.6，大家猜猜我提了一个什么问题呀！

生：买①号笔记本和③号笔记本能找回多少元？

根据学生反馈交流，黑板呈现如下六道算式：

12.4+6.62 7.6-6.62

50-12.4 12.4+6.62+7.6

50-（6.62+7.6） 50-12.4-7.6

小结：同学们都好厉害啊！不仅能通过自己提问列出算式，而且还能根据别人的算式知道别人提了什么问题！

【设计意图：通过生生互动、师生互动呈现算式，理解问题。六道算式精心设计，既有一步计算的，也有两步计算的。其中，一步计算的有整数部分相减为0的，有整数减小数的；两步计算中有可以简算的，也有不能简算的，为后续知识梳理提供结构性材料。】

二、分类梳理，形成知识结构

1．组织分类，根据运算的步骤将六道算式分为一步计算和两步加减混合运算。

2．梳理一步计算的竖式计算。

（1）学生结合问题解决中的“12.4+6.62，7.6-6.62，50-12.4”三道算式，独立列竖式计算，指名板演。

（2）反馈，介绍小数加减法竖式计算方法，强调：小数加减竖式计算，小数点对齐。

（3）算理跟进：同学们都知道算的方法，那你知道算的道理吗？

出示算式并计算：0.3+0.4

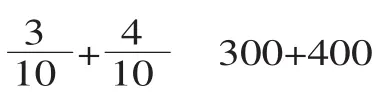
师：说说这几道算式有什么相同的地方？

生：都是3加4等于7。

师：每道题目中的“3”“4”“7”分别表示什么？

生：三道算式分别是“3个0.1加4个0.1等于7个0.1，3个加4个等于7个，3个百加4个百等于7个百”。

小结：看来不管是小数、分数还是整数的加减法，都是相同计数单位的个数相加减。

【设计意图：通过学生竖式计算对算法进行查漏补缺，并通过小数加法、分数加法和整数加法的三道算式跟进，使学生感悟到不管是小数、分数还是整数，其加法的本质都是通过相同计数单位的个数累加而来，从而进一步理解算理。】

3.梳理两步加减混合运算。

（1）观察“12.4+6.62+7.6，50-（6.62+7.6），50-12.4-7.6”三道题，思考：哪道题比较容易计算？

（2）学生通过数据观察，找到能简算的算式并独立计算三题，指名板演。

（3）反馈交流，介绍计算的方法和依据。

结合“50-12.4-7.6”复习减法性质，结合“12.4+6.62+7.6”回忆加法交换律和加法结合律。指出，运算律和运算性质能改变混合运算中的运算顺序，是简算的依据。

（4）跟进：不计算，判断算式得数的大小。

出示“17.6-6.25+3.75，17.6-（6.25+3.75），17.6+6.25+3.75”，不计算判断哪道题得数最大、哪道题得数最小，为什么？

学生找出算式，并说理。观察比较第一题和第二题，有什么相似之处，计算中需要注意什么。

（5）梳理小结。

通过刚才的梳理，我们知道了小数加减法算的方法和算的道理。列竖式计算时，小数点要对齐，也就是相同数位对齐，这是因为计算中是相同计数单位个数相加减。在混合运算中，能简算的要先简算，不能简算的就按顺序计算，这是因为运算律可以改变混合运算的运算顺序。

【设计意图：先通过题组中“哪道题比较容易计算”的判断引发学生对数据进行思考，卷入简算算法的复习；然后通过简算算理的讨论，进一步明确运算律和运算性质可以改变混合运算中的运算顺序。而在另一题组判断得数大小中，强调小数加减混合运算中注意观察数据和运算顺序，从而判断并选择合理算法。】

三、巩固内化，发展思维能力

1．看图写算式。

课件依次呈现方格图、计数器图、单位转化图示，学生解读图示列出算式。

小结：不管是格子图、计数器图，还是单位转化，都需要找准每个数或图示所对应的计数单位是什么。

【设计意图：通过不同的图示表征，解读小数意义和运算含义，帮助学生再次理解小数的加减法其实就是相同的计数单位个数相加减。】

2．算一算，想一想。

下图每条线上都有三个数。那么相加正好等于1的是_____，接近18的是_____。

【设计意图：三个数相加正好是1的算式，让学生感悟到每个加数都必须小于1，从而缩小寻找范围；和接近18的算式，可以通过排除、估算等方法得到，培养学生的估算意识，发展数感。】

3．解决问题。

（1）接力赛中的问题。

出示问题，学生列式计算，反馈交流。

小结：四个小数相加，求得结果有多种方法。可以通过加法的交换律和结合律改变运算顺序，实现简便计算。

（2）发票中的问题。

师：这张发票弄脏了，你能根据已知的数据把它填完整吗？你会先算哪一格呢？

生：我会先算第④格，再算第③格，然后求出第②格和第①格。

生：我会先算第③格，再算第④格，然后求出第②格和第①格。

指名介绍推算过程，并校对答案。

【设计意图：第一题，通过接力赛总成绩不同计算方法，强调算法多样性和创新性；第二题，通过多条路径的数据推算，培养学生的推理能力，反映了运算的本质是推理。两道练习设计，重视了具体实际问题解决中运算能力的培养和思维的训练。】