地震作用下的边坡稳定性分析

李灿阳

（广州市南沙区磨碟头工程管理所，广州510000）

每年由地震引起的滑坡对我国国民经济和人身安全造成巨大损害。因此，研究边坡在地震下的稳定性问题具有重要意义。目前，把岩土看成理想塑性的Mohr-Coulomb材料， 使用强度折减法或地震超载法对边坡进行有限元分析是目前最为常见的两种边坡动力稳定性分析方法。 强度折减法假定地震荷载不变，改变边坡强度以搜索边坡临界强度，边坡现状强度和临界强度相比来衡量边坡的强度储备程度，郑颖人［1］、叶 海林［2］、戴妙林［3］等 采用强度 折 减 法 对 边坡的动力稳定性进行了分析研究。 地震超载法不改变边坡现有强度， 通过改变地震荷载以搜索结构破坏面及其对应的临界荷载， 将临界荷载与标准荷载之比定义为临界动力超载倍数， 以此判断结构安全性能，孙进忠［4］、胡克梅［5］等采 用了地 震超载法对边坡的动力稳定性进行了分析研究。 强度折减法计算结果可称为边坡强度储备稳定性， 地震超载法计算结果可称为边坡动力超载稳定性。 本文以国内某水利工程中的右岸边坡为研究对象， 以塑性区贯通为失稳判别标准［4，6］，分别采用强度折减法和地震超载法对边坡的动力稳定性进行了研究。

1 计算理论与方法

1.1 强度折减法

强度折减法假定地震荷载不变， 把边坡现状抗剪强度参数（c，φ）等比例折减k倍，然后用折减之后的边坡抗剪强度参数（c1，φ1）进行动力时程分析，计算公式如下：定义使边坡达到临界动力失稳状态时对边坡抗剪强度参数的折减程度F为动力安全系数。

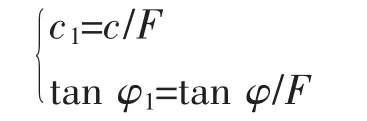
1.2 超载系数法

动力超载系数法不改变岩土材料参数， 对地震荷载不断地进行加载，直到边坡临界失稳，定义此时的地震荷载超载系数即为边坡的动力安全系数。 计算公式如下：

a′=K·a

式中 K为超载系数；a和a′分别为边坡设防地震峰值加速度和边坡临界破坏时的地震峰值加速度。

2 实例应用

2.1 工程概况

某水利工程坝址区右岸边坡永久性坡高68m左右，开挖前平均坡脚27°，开挖后坡脚为38.7°，开挖后分设5级马道。 边坡岩体主要为千枚岩，由表及里共分全夹强风化带、强风化带及弱风化带3个分带。 经监测资料分析，此边坡稳定性不高，浅表层岩体易发生滑动。 此边坡工程地质剖面示意图如图1。

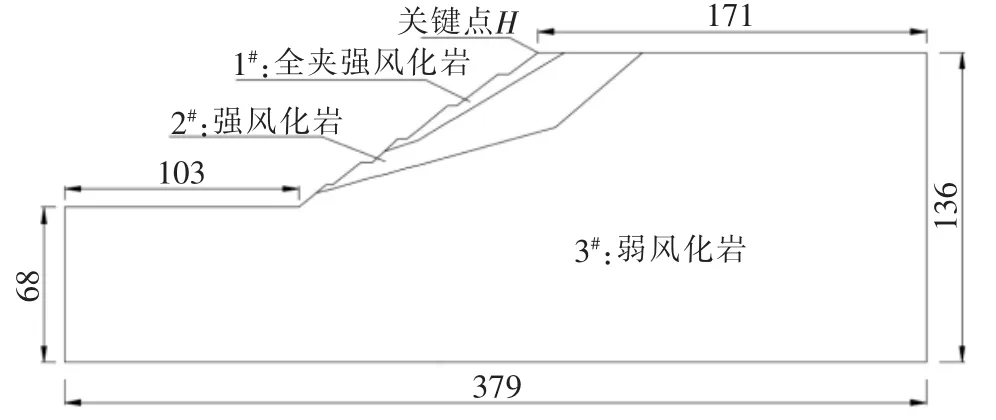
图1 边坡工程地质剖面示意图

2.2 边坡有限元模型的建立

合理的有限元边界范围设定会使仿真结果与工程实际结果更为接近， 本文依据郑颖人的研究成果［7］，建立边坡有限元模型如图2：坡高H=68m，坡脚至左边界距离、坡顶至右边界距离、上下边界距离分别取为坡高H的1.5倍、2.5倍、2倍，即分别为103，171，136m。

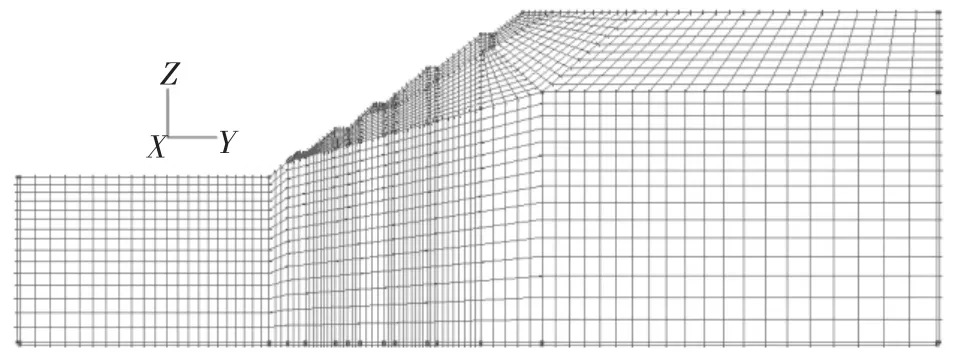
图2 边坡有限元模型

边坡采用Mohr-Coulomb屈服准则， 底部及四周设置等效一致黏弹性边界［8］，以真实反映远域地基辐射阻尼对地震波的影响，地震波从底部输入。岩土体具体参数如表1。

表1 岩体材料物理力学参数

本文基于规范反应谱［9］以阻尼比5%，动力放大系数βmax=2.5合成一组水平向峰值加速度为0.2g和竖向峰值加速度为0.133g人造地震波。人造波持时20s，计算步数为2000，步长0.01s，如图3。

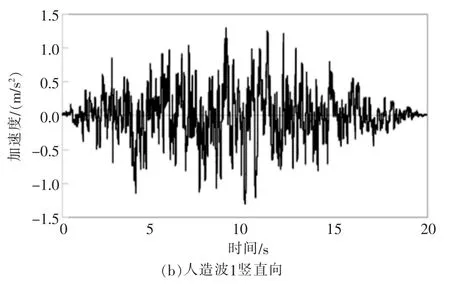
图3 地震加速度时程曲线

3 仿真结果分析

3.1 强度折减法仿真结果

折减系数从1.3～1.88时的边坡塑性区分布如图4。

图4 强度折减法塑性区分布

从图4可看出，随着折减系数的不断增大，塑性区先从边坡软弱部分开展，然后不断向周围扩展，当折减系数达到1.88时，塑性区刚好贯通坡顶，可判定该边坡的强度折减安全系数为1.88。 塑性区主要产生于边坡1#全夹强风化岩和2#强风化岩部分。

3.2 地震超载法仿真结果

超载系数从2～3.2时的边坡塑性区分布如图5。

图5 地震超载法塑性区分布

从图5可看出，随着超载系数的不断增大，塑性区先从坡脚和坡体软弱部分开展， 然后不断向周围扩展，当超载系数达到3.2时，塑性区刚好贯通坡顶，可判定该边坡的超载安全系数为3.2。 塑性区范围主要产生于边坡1#全夹强风化岩和2#强风化岩部分及坡脚处弱风化岩部分。

对比以上两种计算方法可发现： 当塑性区刚好贯通坡顶时， 地震超载法计算出的塑性区范围产生于边坡1#全夹强风化岩和2#强风化岩部分以及坡脚处弱风化岩部分， 而强度折减法计算出的塑性区范围主要产生于边坡1#全夹强风化岩和2#强风化岩部分， 由此可见地震超载法计算出的边坡塑性区范围要大于强度折减法计算出的边坡塑性区范围。

4 结语

（1）以边坡塑性区贯通坡顶为失稳判别标准，分别采用强度折减法和地震超载法对该边坡进行稳定性研究， 可判定该边坡的强度折减安全系数和地震超载安全系数分别为1.88和3.2。

（2）当塑性区刚好贯通坡顶时，地震超载法计算出边坡塑性区范围要大于强度折减法计算出的边坡塑性区范围。