修正的横观各向同性千枚岩岩体强度破坏准则

王洪新

（山西晋城公路规划设计院，山西 晋城048000）

1 背景

层状岩体的力学特性会随着倾角的不同而发生变化，分析层状岩体变形和破坏特征，解决工程岩体的失稳问题，是岩土研究的核心问题，建立合适的强度准则是解决这一问题的基础。 众多学者基于连续介质思想，在各向同性材料的基础上，将力学参数变为与层理倾角有关的函数， 从而模拟层状岩体的横观各向同性性质。 Jaeger［1］将黏聚力看成是随层理面倾角变化的函数， 而将摩擦角看成是常数， 对传统Jaeger理论进行了完善；张贵科［2］、杨强等［3］用损伤张量表示节理连通率， 并根据连通率对Mohr-Coulomb强度准则中的粘聚力和内摩擦系数进行等效替换，进而建立了各向异性节理岩体的抗剪强度屈服准则；常江芳等［4］认为横观各向同性材料的弹塑性本构方程是材料组构张量、大主应力方向的函数，提出了适用于横观各向同性岩体的改进D-P准则。 目前常用的各向异性，包括以下几种：

1.1 Hoek-Brown强度准则的修正

Hoek和Brown通过对大量的岩石三轴试验资料和岩体的现场试验结果的统计分析， 提出了Hoek-Brown强度准则，其一般表达式如式（1）：

式中 σ1和σ3为岩石破坏时的最大和最小主应力；σci为岩石单轴抗压强度；mb，s和α为岩体材料常数。对完整岩石mb等于材料常数mi，s=1和α=0.5。

为了反映岩石强度各向异性特征，Hoek和Brown认 为mb和s 的 值 随 层 理 倾 角 而 变 化。 Saroglou 和Tsiambaos［5］指出对于强度各向异性的岩石计算mb和s繁重而枯燥，并通过直接引入修正因子kβ，对Hoek-Brown强度准则进行了修正，如式（2）：

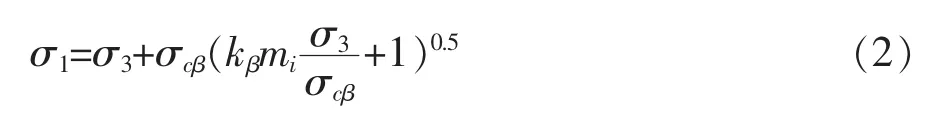
式（2）在下文中采用HB1表示， σcβ为岩层走向与主应力方向夹角为β时的单轴抗压强度，kβ为强度的各向异性系数。 岩层倾角β为90°时，各向异性系数取1，即k90=1.0，并采用β=90时的三轴数据拟合参数mi，其他角度的参数kβ根据试验数据，利用式（2）拟合求得。

Xiangchao Shi和Xu Yang［6］重新对Hoek-Brown强度准则进行了修正，其表达如式（3）：

式（3）在下文中采用HB2表示，αβ为各向异性影响因子。σci为最大单轴抗压强度，根据试验结果，当β等于0°或90°时取得最大抗压强度值，则σci取σc0和σc90中的最大值。当σci=σc0时，则α0=0.5，mi根据β=0时的三轴试验结果拟合求得；当σci=σc90时，则α90=0.5，mi根据90°时的三轴试验结果拟合求得。 其余角度的αβ根据试验数据，利用式（3）拟合求得。

1.2 Ramamurthy强度准则

Ramamruthy 等［7］提出了一种经验性的强度准则用于预测完整各向异性岩体强度的非线性特征，如式（4）：

式中 Bβ和αβ为反映岩体各向异性的材料常数，可以通过式（5）～式（6）计算：

式中 σc90为岩层倾角β=90°时的单轴抗压强度；α90和B90为岩层倾角β=90°时Bβ和αβ的值。

由于实际工程中， 室内试验获得的参数往往是有限的，且多为低围压下的试验结果，本文旨在提出一种各向异性强度准则， 依靠有限的试验数据获得的参数，能够较好的预测岩体在多围压下的强度。

2 新型修正的各向异性强度准则

Z.T.Bieniawski［8］基于大量的岩石三轴压缩试验提出了一种经验性的强度准则，如式（7）：

式中 σc为单轴抗压强度；A为无量纲系数， 为岩体材料常数。

式（7）是基于各向同性的岩石提出的经验性强度准则，为反映岩层的各向异性，可参照式（2），即HB1的方式，直接引入各向异性系数Rβ对式（7）进行修正，如式（8）：

式中 Rβ为强度的各向异性系数。 岩层倾角β为90°时，各向异性系数取1，即R90=1.0，并采用β=90时的三轴数据拟合参数A， 其他角度的参数Rβ根据试验数据，利用式（8）拟合求得。

3 拟合结果的评价标准

采用三种误差指标评价拟合结果， 第一种误差指标为均方差（R2）：

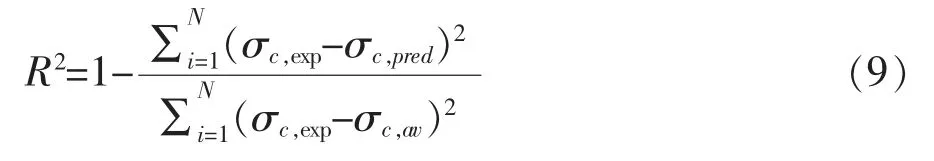
式中 N为室内试验的总个数；σc，exp为室内试验峰值强度；σc，pred为理论计算预测强度；σc，av为室内试验平均峰值强度。

第二种误差指标为单个数据的误差：

第三种误差指标为绝对误差的平均值：

根据三种误差表达式的含义，越小，则计算模型的准确性越高。 另一方面，R2越高，理论值与试验值的相关性越好， 所以较低的AAREP往往对应一个较高的R2。通过计算AAREP的最小值，得到最优的拟合参数。

4 拟合结果及其讨论

4.1 拟合参数的敏感性分析

强度准则中参数［式（2）中的mi和kβ；式（3）中的mi和αβ；式（4）中的Bβ和αβ；式（8）中Rβ和A］拟合的正确性直接影响到强度准则的正确性。 工程实践中常采用回归分析的方法拟合出相关参数，因此，室内试验数据的数量很大程度上影响参数的拟合结果和理论计算的准确性。当只有低围压的室内试验数据时，拟合结果如不能真实反映岩石的强度包络线， 则强度准则的正确性会降低。正是处于这种考虑，Singh［9］特别指出，强度准则的参数对围压敏感度越低越好，以达到采用较少的低围压下室内试验结果拟合出的参数也能准确的预测高围压下峰值强度的效果。

本文采用Mahendra Singh［10］千枚岩的室内试验结果，如图1。

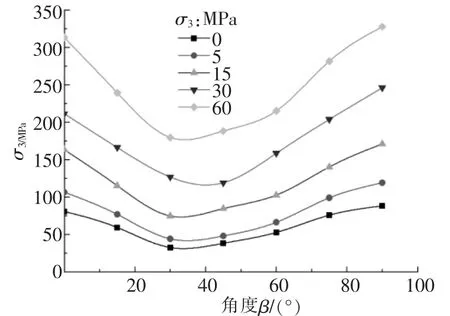
图1 千枚岩室内试验结果

由图1可知， 共进行了单轴压缩试验和围压为5，15，30，60MPa4种围压的室内试验。 本文采用从低到高不同数量的围压组合， 根据AAREP最小的原则拟合对应围压下的室内试验数据得到相应的拟合参数， 再采用得到的拟合参数预测所有围压的室内试验结果， 针对千枚岩采用3种组合， 即AQ1 （σ3=5，15MPa）；AQ2 （σ3=5，15，30MPa）；AQ3 （σ3=5，15，30，60MPa），拟合得到的不同准则的参数如表1。

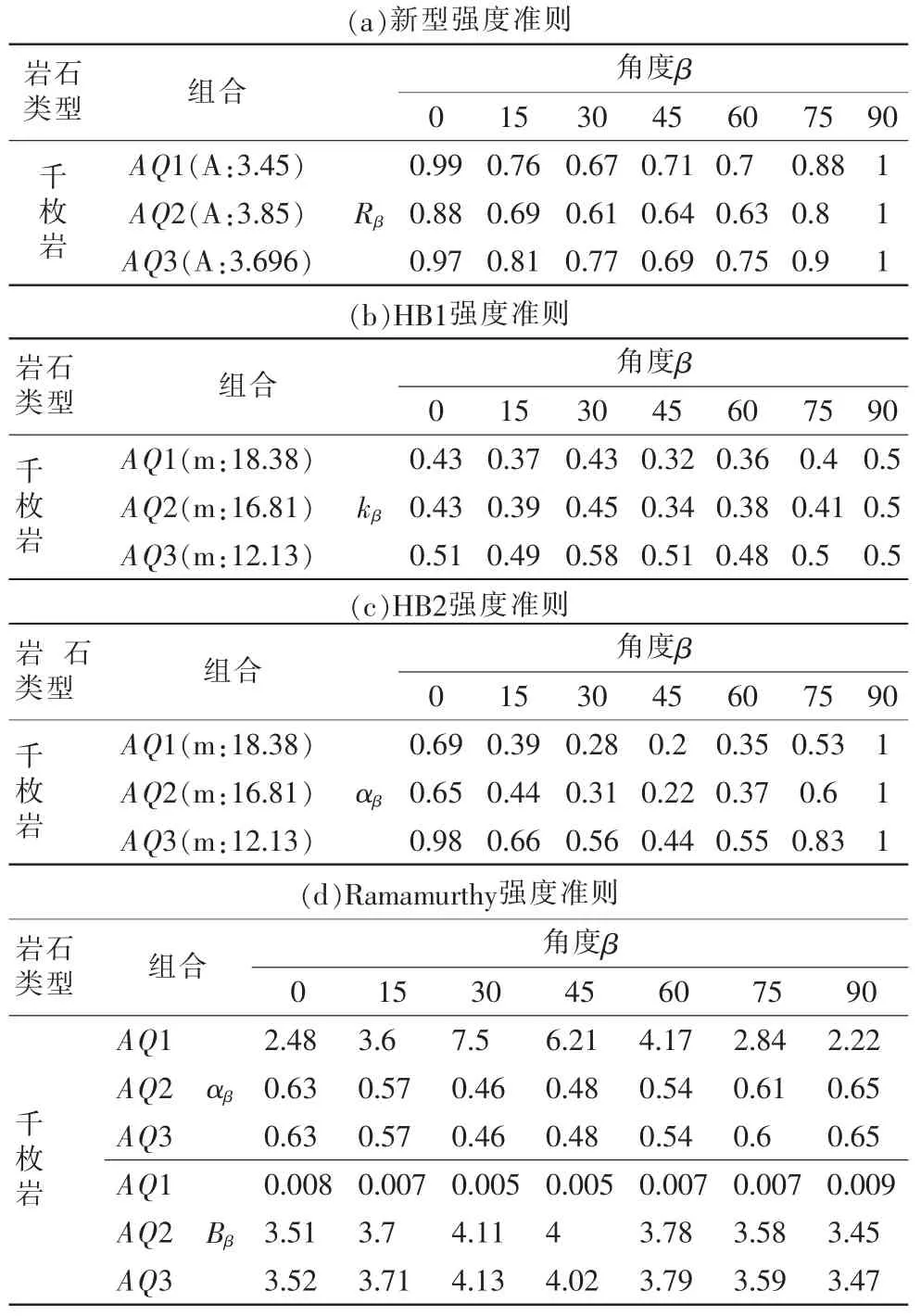
表1 三种组合不同强度准则的拟合参数

标准差的大小反映了数据的离散程度，可通过计算表1中不同强度准则下参数的标准差以反映围压对拟合参数的影响，计算表达式如式（12），标准差越小，代表了其离散程度越小，即拟合参数对围压越不敏感。 不同强度准则下参数标准差的大小如表2。

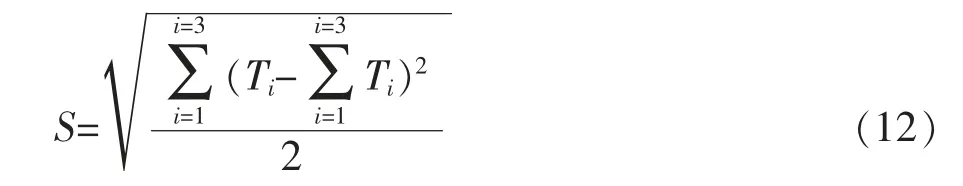
式中 Ti为拟合参数值。

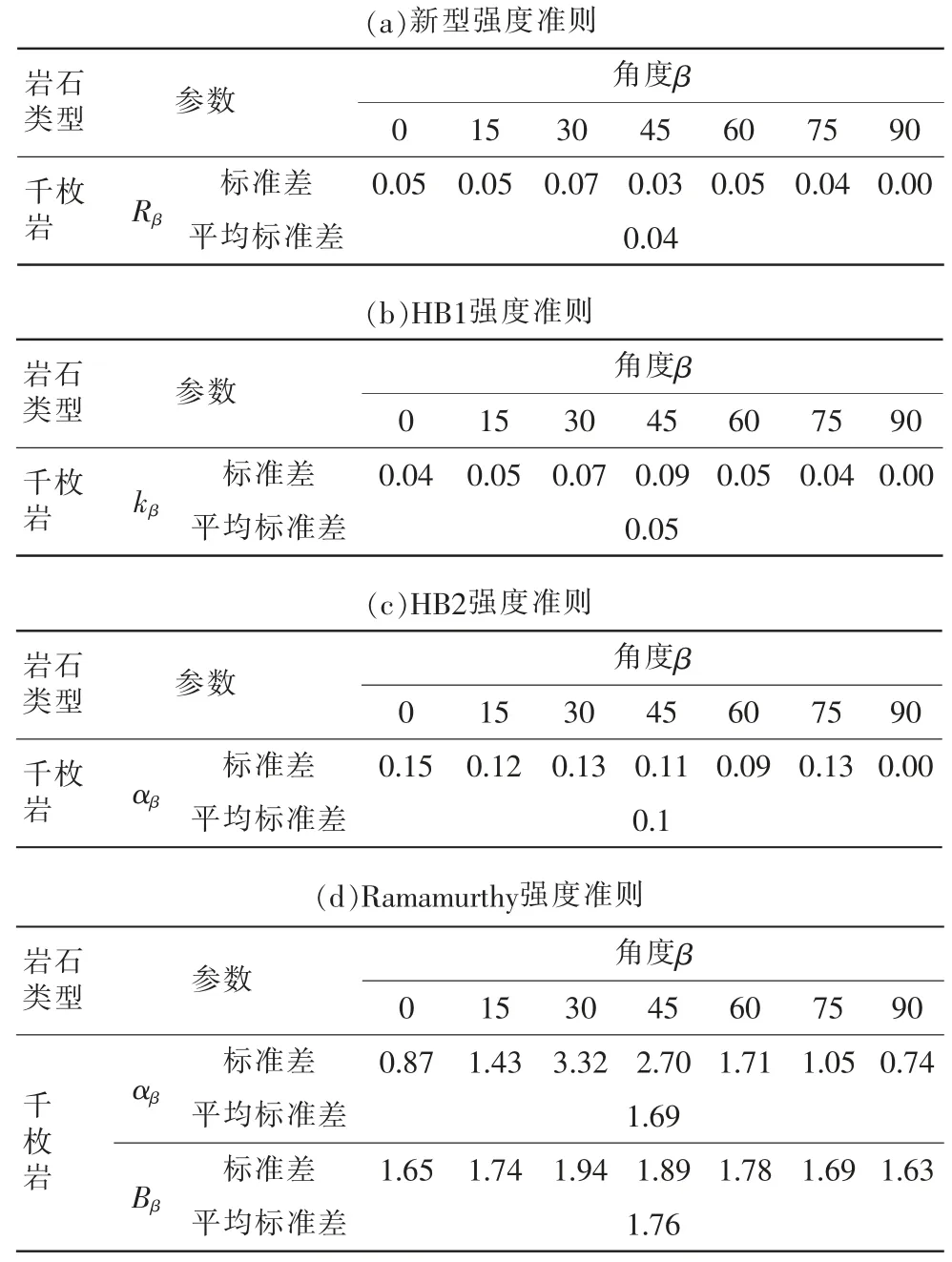
表2 三种组合不同强度准则的各向异性指数标准差

从表2可看出，新型强度准则各向异性指数的平均标准差为0.04， HB1强度准则的平均标准差为0.05，HB2强度准则的平均标准差为0.1，Ramamurthy强度准则两参数平均标准差分别为1.69和1.76，不难看出新型强度准则的标准差最低。

采用类似的方法可以计算出， 新型强度准则参数A、HB1和HB2强度准则参数的标准差分别为0.16和2.65，新型强度准则的标准差较小。

4.2 峰值强度拟合结果对比

采用上节中AQ1，AQ2，AQ3 3种组合拟合的参数，利用新型强度准则式（8）预测所有围压的室内试验结果，拟合结果如图2。

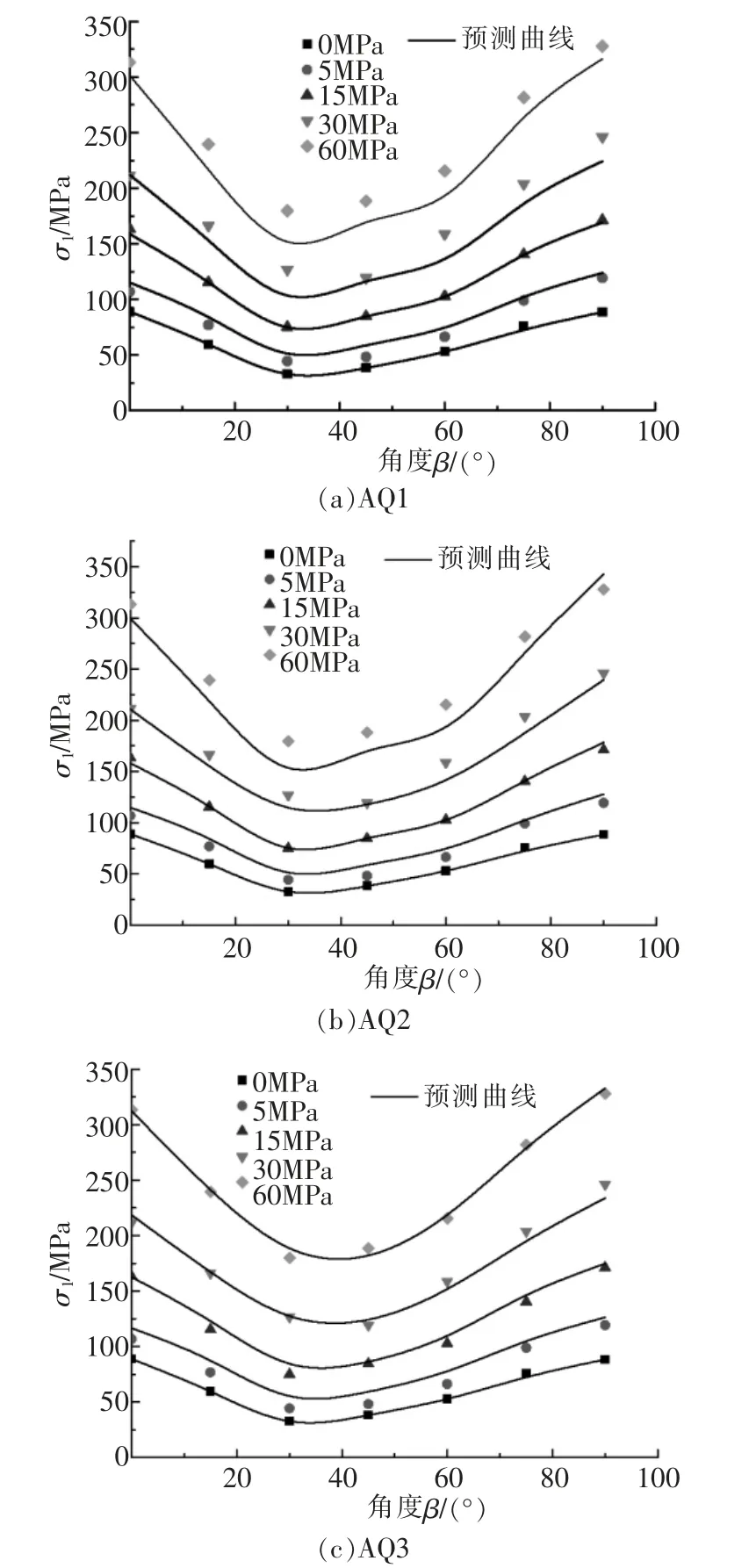
图2 不同组合试验值与理论计算值对比

由图2可知，不同围压组合下的拟合参数得到的预测值均与室内试验较为吻合； 随着室内试验数据的增加，拟合结果与试验值更为吻合。 为了更好的说明新型模型的优越性，将AQ1，AQ2，AQ3三组围压组合拟合的参数， 采用不同的强度准则预测所有围压的室内试验结果，如图3，4，5。 其中拟合参数下Ramamurthy的预测值偏差过大， 这里不予列出。

由图3可知，采用二组试验数据拟合出的参数用于预测室内试验全部围压的峰值强度， 本文新型强度准则的均方差R2为0.96，AAREP为5.85%；HB1强度准则的均方差R2为0.93，AAREP为7.86%；HB3强度准则的均方差R2为0.96，AAREP为6.08%；Ramamurthy强度准则偏差过大，不予列出。 由计算结果看出，采用较少试验数据， 本文新型强度准则的预测误差小于其他强度准则。

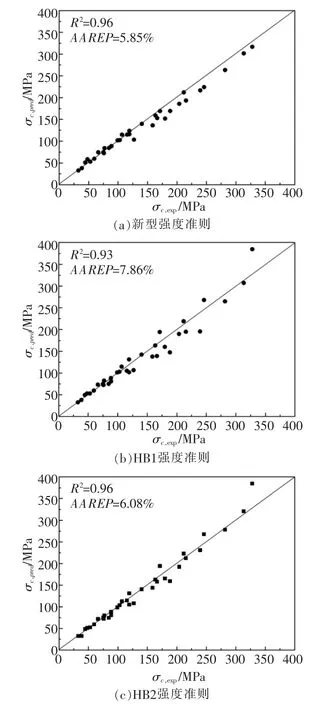
图3 拟合参数预测结果

由图4可知，采用三组试验数据拟合出的参数用于预测室内试验全部围压的峰值强度， 本文新型强度准则的均方差R2为0.97，AAREP为5.80%；HB1强度准则的均方差R2为0.95，AAREP为6.48%；HB3强度准则的均方差R2为0.97，AAREP为6.52%；Ramamurthy强度准则的均方差R2为0.81，AAREP为12.4%。 由计算结果看出，HB2强度准则的误差最小，本文强度准则次之，但两者相差不大。

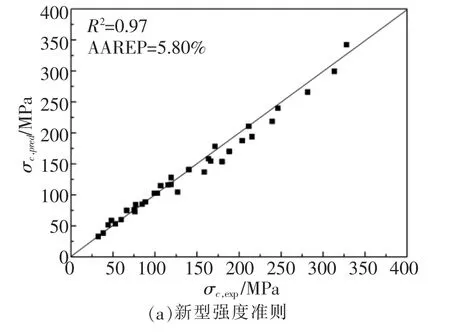
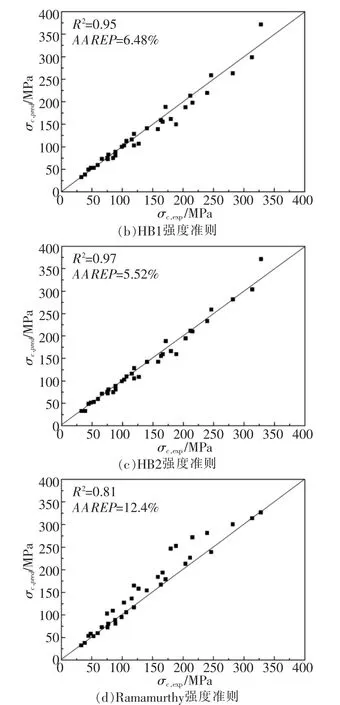
图4 拟合参数预测结果

由图5可知，采用全部试验数据拟合出的参数用于预测室内试验全部围压的峰值强度， 本文新型强度准则的均方差R2为0.99，ARREP为5.01%；HB1强度准则的均方差R2为0.99，ARREP为3.46%；HB3强度准则的均方差R2为0.99，ARREP为4.03%；Ramamurthy强度准则的均方差R2为0.81，ARREP为12.3%。 由计算结果看出，HB1强度准则的误差最小，HB2强度准则准则次之， 本文新型强度准则的误差虽不及HB1和HB2强度准则正确，但三者相差不大。

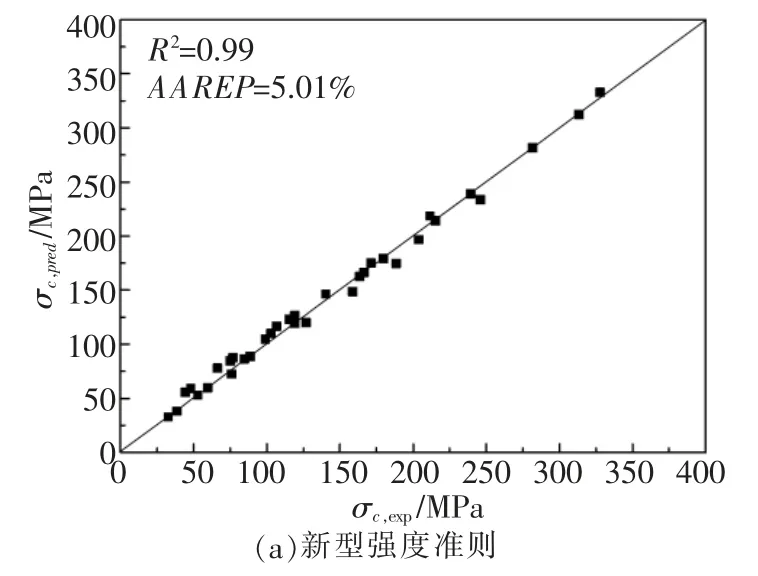
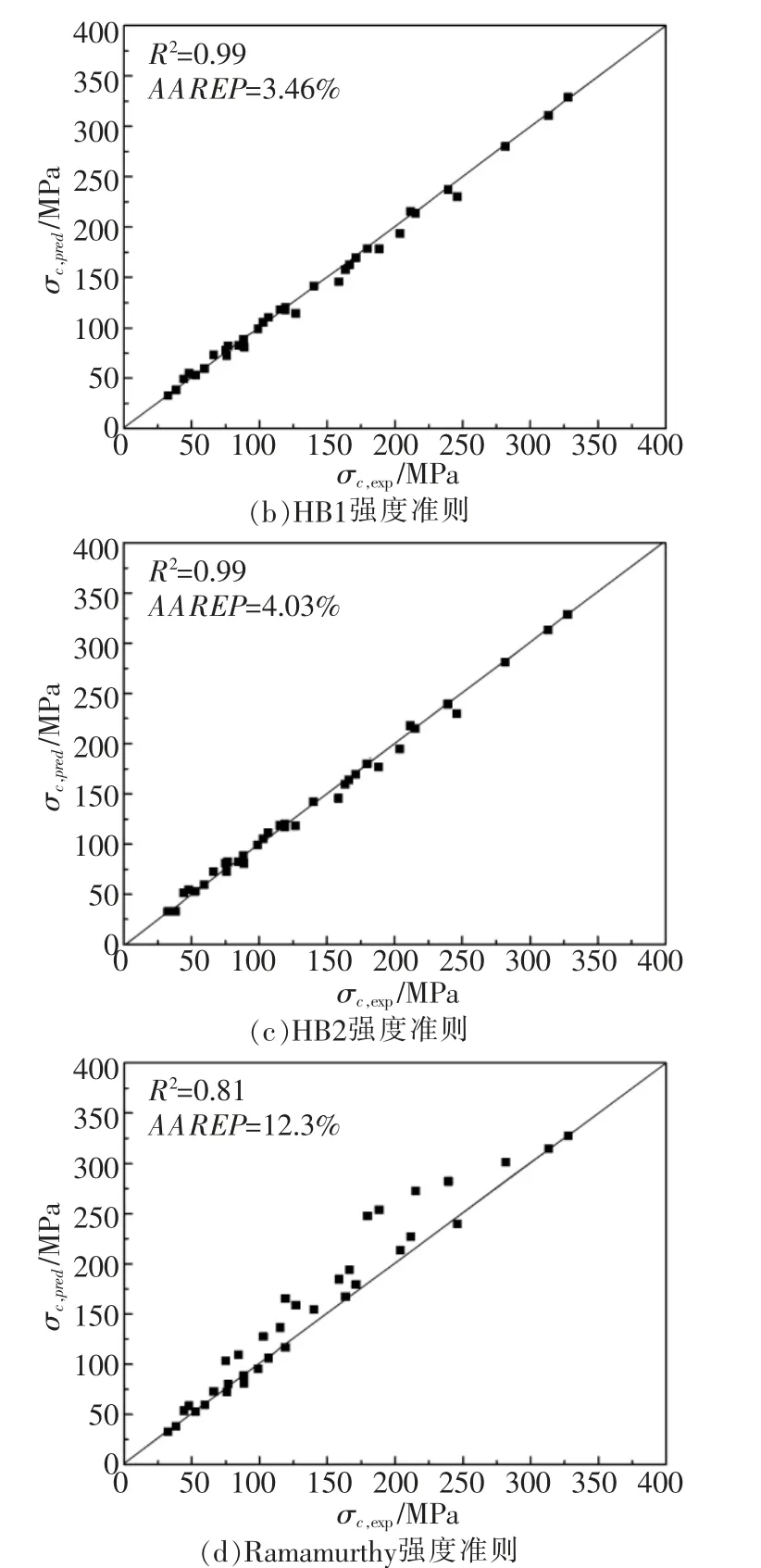
图5拟合参数预测结果

由此可见， 本文的新型强度准则可以较好的预测各向异性岩石的峰值强度， 特别是室内试验数据缺乏时，采用本文强度准则得到的峰值强度，其准确性最高。

5 结语

本文根据层岩强度的各向异性， 提出一种修正的强度准则， 并与目前常用的修正Hoek-Brown强度准则以及Ramamurthy强度准则进行对比。 计算结果表明，本文提出的强度准则，采用有限的试验数据，进行预测时，表现出较高的相关性以及较低的误差，本文提出准则参数对围压敏感度较低， 达到了采用较少的低围压下室内试验结果拟合出的参数也能准确的预测高围压下峰值强度的效果。