对《公路排水设计规范》中几个有关地下排水水力计算公式的讨论

尚许雯，尚银生，张晓景

(1.山西省交通规划勘察设计院，太原 030012；2.山西省勘察设计研究院，太原 030013)

2013年实施的JTG/TD 33—2012《公路排水设计规范》[1](以下简称《规范》)，将原规范[2]中水文计算与水力计算的内容合并为一章，补充了地下排水设施的流量计算和水力计算等方面的内容。但在此过程中，一方面未对原规范中几个主要流量计算公式中的不合理部分予以修改、完善，而直接保留引用；另一方面，新增加的渗井计算部分也有需要修改之处。

1 关于渗井计算部分

《规范》提出：位于含水层内的单位长度渗井的流量Qs应按式(1)计算确定，图示说明见《规范》图9.4.6含水层内渗井的流量计算。

(1)

式中，Qs—单位长度渗井的流量，m3/(s·m)；hj—井内水深，m;hd—地下水位高于井底的高度，m;r0—渗井半径，m；Kh—含水层材料的渗透系数，m/s；R—影响半径，m，可根据抽水试验确定，或用下列经验公式计算：

(2)

式中，S—抽水降深，m，即地下水位与井内水位的高差。

对于渗水井：

S=hj-hd

(3)

首先，式(1)为稳定流潜水完整井流量计算公式，等式右侧是流量的量纲L3T-1，并非单位长度渗井的流量量纲L3T-1L-1，因此所计算的流量为渗井流量，而非单位长度渗井流量。

其次，式(2)是吉哈尔特影响半径经验公式，一般认为适用于承压水的影响半径计算，因此将潜水完整井流量计算公式与承压水影响半径经验公式联立求解是不合理的，而应选择与式(1)配套的库萨金经验公式来计算影响半径：

(4)

式中，H0—潜水含水层厚度，m；K—渗透系数，m/d；其它参数意义同上。

第三，式(1)是一个潜水完整井流量计算公式，而《规范》图9.4.6并未体现出完整井的水文地质结构，甚至不能反映其水力性质为潜水。因此，式(1)不能直接利用《规范》图9.4.6所示的hj、hd而加以计算；更需要考虑的是：当渗井所填滤料的渗透系数与下伏含水层渗透系数差异较大时，应按非均质含水层计算下渗量。

《规范》提出按下式估算渗井孔径D：

(5)

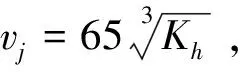
(6)

式中，νj—井壁允许进水流速，m/s；K—含水层平均渗透系数，m/s。

一般认为该式为阿勃拉莫夫井壁进水流速计算值的1/3～1/2,通过生产井的实际复核，式(6)更符合我国供水管井、渗井的实际情况。因此，若有必要估算渗井孔径，建议将井壁进水流速部分对应修改，即将式(5)修改为：

(7)

按照《规范》式(5)进行计算时，其流速的单位是错误的。由于其中Kh的单位已选择为m/d，以此相应的设计流量Qs的单位应为m3/d，而非m3/s。

2 关于不透水层横向坡度较陡时的流量计算

《规范》提出的公式为：

Qs=Kh·ih·hs

(8)

式中，ih—水力坡度；hs—渗沟位置处地下水位的下降幅度，m。

图示说明见《规范》图9.4.3不透水层的横向坡度较陡时的渗沟流量计算。

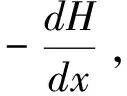
=Khhmi

(9)

式中，h1、h2—上下游断面1、2的渗流厚度，m；hm—上下游断面1、2间过水断面的平均厚度；H1、H2—上下游断面1、2以水平轴起算的水头高度，m；l—渗流长度，m；i—上下游断面1、2间的水力坡度。

式(9)即卡明斯基近似式。式(9)虽然与式(8)形式相似，但所反映的本质还是有所区别的。hs是水位降深，不是过水断面，因此不能用断面法来进行流量计算，而应按过水断面的平均厚度hm来计算。

(10)

与另一水文地质模型式(11)的表现形式相同，也说明式(8)不合理，它不能反映不透水层水平时应该有的表现形式。

3 当渗沟沟底设在不透水层上或不透水层内时的流量计算

相应的一组公式：

(11)

(12)

(13)

(14)

式中，Qs—单位长度渗沟一侧沟壁的地下水渗入量，m3/(s·m)；hc—含水层内地下水位的高度，m；hg—渗沟内的水流深度，m，当渗沟底位于不透水层内，且渗沟内水面低于不透水层顶面时按式(12)取用；Ls—地下水位受渗沟影响而降落的水平距离，m；I0—地下水位降落曲线的平均坡度，可按含水层材料的渗透系数由近似公式(14)估算。图示说明见《规范》图9.4.1不透水层坡度平缓时的渗沟流量计算。

笔者对《规范》9.4.1条一些水文地质条件假设是存在疑义的。无论稳定流还是非稳定流理论，无论是承压水还是潜水，都没有采用地下水自然流动速度近于零的假设；而且地下水自然流动速度近于零与否，与不透水层的横向坡度较小没有必然的联系。地下水渗流理论中相应的假设为地下水天然水力坡度为零[7-9]，以方便公式的推导与建立，两者之间有联系，但明显意味不同。

当(hc-hg)与Ls相比很小时，可以认为式(13)是正确的。

将式(12)进行一些变化，可以得出

(15)

(16)

并对照式(11)，可以得出Qs=Kh·hg。这是一个表面正确，但没有考虑过水断面变化及水力坡度的公式，显然是不合理的。此外，即便沟底设在不透水层内，式(13)同样基本正确、适用，因此式(12)是不合理的，且似乎没有提出的必要。

4 关于渗沟沟底距不透水层顶面较远时的流量计算

图示说明见《规范》图9.4.2。

(17)

式中，Ll—两相邻渗沟间距之半，m；Hs—渗沟位置处地下水位的下降幅度，m。

显然2Ls与Ll的大小关系是明确的，为了满足公式的需要，应该2Ls>Ll，即两相邻渗沟处于影响范围内，互有影响才可以利用式(17)进行流量计算。但两相邻渗沟间距为2Ll，2Ls与2Ll的大小关系是不明确的，至少《规范》图9.4.2看不出，因此式(17)与《规范》图9.4.2应有一些关联性的修改。而当2Ls<2Ll时，即两渗沟之间无影响或水力联系，单位长度流量计算公式可按以下公式计算：

当渗沟沟底距不透水层顶面较远时，对照《规范》图9.4.1与图9.4.2，当不考虑另一侧排水渗沟影响时，

(18)

说明是巨厚含水层中的潜水水力性质的渗沟，井中降深仅占潜水含水层厚度的很小部分，因此，一个渗沟、一侧进水的单位长度流量计算公式如下：

(19)

hc+hg≈2hc

(20)

Sw=hc-hg

(21)

因此，当两条渗沟两侧排水时的单位长度流量计算公式为：

Qs=4hcKnSw/Ls

(22)

5 结论

笔者认为，《规范》将潜水水力计算公式与承压水影响半径吉哈尔特经验公式联立求解有关参数是欠合理的；机械地理解了假定的水文地质条件，未能合理地将这些假定条件应用于公式计算中；对一些假定的水文地质条件存在疑义，部分图示条件不能说明相应公式是正确运用的，或者说式、图不一致，部分应为相互关联的公式，因而出现矛盾；按阿勃拉莫夫含水层井壁允许进水流速估算渗井孔径不够合理。过大的井壁进水流速易导致含砂量加大，难以保证渗井长期正常运行使用；应按卡明斯基近似式计算不透水层和水平底板有一定夹角的流量计算。