基于活性炭吸脱附测试的杜比宁吸附方程修正表达式

李振海, 裘舒年, 李 姗, 陈 瑶

(1.同济大学 机械与能源工程学院,上海 200092;2.奥雅纳工程咨询(上海)有限公司,上海 200052)

随着我国经济的发展,室内空气质量(indoor air quality,IAQ)问题成为人们关注的焦点[1].室内建材及建筑装修材料散发出大量的挥发性有机化合物(volatile organic compounds,VOC)严重恶化了室内空气质量,采用空气净化器去除VOC是一种改善空气质量的有效方法[2].最常见的是应用以活性炭为主的多孔物理吸附材料的物理吸附净化方法.该方法已被证明适宜用于处理室内成分复杂的气态污染物,且与催化氧化法相比,在净化过程中不会产生其他的污染物质造成二次污染[3].活性炭吸附VOC的效果已被许多研究证实.李立清等[4]研究证实了使用微波改性活性炭有助于提高活性炭对甲醇的吸附作用.闫奔等[5]通过实验验证了活性炭对乙醇和甲苯的吸附作用.

物理吸附根据其性质的不同,可以分为单层分子层吸附、多层分子层吸附、毛细凝聚和微孔充填4种形式[6].由于活性炭中微孔比例较大,故活性炭吸附VOCs的过程主要为微孔吸附,微孔充填理论可以有效地解释微孔中物理吸附行为[7].

以微孔活性炭为模型而建立的杜比宁吸附方程(Dubinin-Radushkevich方程,D-R方程)在计算微孔吸附量并判断吸附剂微孔结构特征时具有很好的适用性[6,8].李海龙[9]通过实验方法研究了活性炭C40/4对丙酮、甲苯、二氯甲烷三种有机气体的吸附性能,采用微孔填充理论结合D-R方程分析实验数据并建立吸附等温模型,发现微孔填充理论及D-R方程可很好地描述活性炭C40/4对有机气体的吸附性能,理论预测值与实验测试值误差较小.但当有机气体分压较高时,使用D-R方程得到的预测值较实验测试值偏低.近藤精一等[10]的研究证实D-R方程在低相对压力(P/p0=10-5~10-1)时(P为气体的平衡压力,p0为实验温度下的饱和蒸汽压),计算值和实测数据吻合较好,而在相对分压较高时(相对压力大于10-1),拟合情况较差.由叶青[8]给出的参考数据可以看出,椰壳活性炭,硅胶S-200等微孔吸附材料自相对压力大于0.04起,吸附特性曲线的数据点即开始显著上漂,该部分数据使用D-R方程线性拟合情况欠佳,如文献[8]中的图3.6所示.

由文献[8-10]可见,在高相对压力区(2.59<[ln(p0/P)]2<10),D-R方程对微孔吸附剂的吸附数据点拟合精度较低.因此,本文以D-R方程为基础,提出了活性炭材料在高相对压力区D-R方程的修正表达式,并用8~16目椰壳活性炭、4 mm柱状煤质活性炭、8~30目木质破碎炭三种活性炭材料的吸附实验数据进行实验验证,结果表明在高相对压力区,修正表达式拟合结果比原始D-R方程的准确度更高.

1 D-R方程及修正表达形式的提出

1.1 微孔容积充填理论

依据国际理论化学与应用化学联合会(IUPAC)[11]对吸附剂孔径的分类方法,孔径(直径)2 nm以下的孔为微孔,2~50 nm的孔为中孔,或称过渡孔、毛细孔,而大于50 nm的孔则属于大孔.Dubinin指出,中孔的吸附过程包含单分子层吸附、多分子层吸附、毛细凝聚等多种形式,大孔的吸附过程包含单分子层吸附和多分子层吸附两种形式.而微孔的吸附则与中孔大孔不同,由于微孔孔径与气体分子的直径处于同一数量级,微孔吸附属于微孔充填形式而非表面吸附形式[6,12],其具体特征为:

(1) 微孔吸附不沿表面逐层进行,而是将吸附质分子填充至吸附剂孔隙中[13];

(2) 微孔孔容积决定了微孔吸附剂的最大吸附量[6];

(3) 相比表面吸附形式,微孔充填时,微孔内表面的范德瓦尔势重叠,导致微孔内吸附势比表面吸附更强[10];

相比表面吸附,微孔充填形式下的吸附势更强,微孔在相对压力很低时即能捕捉到吸附质分子[9],因此微孔型吸附剂的吸附等温线被IUPAC划分为I型[10,14-16].

1.2 D-R方程及其使用条件

如1.1节所述,微孔吸附质的吸附机理为微孔充填而非表面吸附,因此基于单分子层和多分子层吸附模型建立起来的langmuir方程和BET(Brunauer-Emmett-Teller)方程不适用于描述微孔吸附[10].为描述微孔充填的相对压力-吸附量特性,Dubinin和Radushkevich提出了一个根据低压区的吸附等温线求吸附特性的方法,其理论基础是Polanyi吸附势理论[9,17].在P/p0<0.2时,Dubinin等进行了多次活性炭吸附气体实验.实验结果显示,当活性炭中包含大量微孔时,CO2在活性炭上的吸附曲线与高斯分布曲线相似[8].

根据D-R方程,在吸附剂微孔中,对气体的吸附方程可用式(1)表示[17]:

(1)

式中:β为亲和系数,与吸附质有关的常数,表示吸附质的吸附势与标准吸附质(苯)的吸附势之比[10];ks为标准吸附质(苯)的基准特征吸附系数;a为吸附质的吸附量,mol·g-1;V0为微孔占多数的活性炭的吸附体积,m3·g-1(当测得中、大孔的比表面积之和小于50 m2·g-1时,可用测试得活性炭的总孔体积表示);v为液态吸附质的摩尔体积,m3·mol-1;p0为实验温度下的饱和蒸气压,Pa;P为气体的平衡压力, Pa;T为实验温度,K;R为通用气体常数,8.314 J·mol-1·K-1

D-R方程使用条件包括:①吸附势ε与温度T没有关系;②吸附温度T远小于临界温度Tc;③微孔占绝大多数(95%以上);④纯物理的吸附过程.

在微污染环境下,有机气态污染物的吸附过程大多都可以满足上述条件,因此可以使用D-R方程.

1.3 现有研究数据的理论分析与本研究的假设

由文献[8]的图3.6可见,在相对压力小于0.04时,D-R方程形式吸附等温线(DR图)数据点线性关系较好,而在相对压力高于0.04的区间内数据点明显上漂.类似的,由文献[10]的图3-26可见,在相对压力小于0.1时,DR图数据点线性关系较好,而在相对压力高于0.1的区间内数据点明显上漂.文献[9-10]对于数据点上漂做出的解释为活性炭吸附氮气出现了毛细凝聚现象.

然而毛细凝聚现象只在中孔中发生[11],且该现象在不同相对压力下对应的发生孔径不同,需要依据开尔文公式(式2)计算.在文献[10]的氮气吸附数据点开始上漂时,相对压力为0.1,对应的开尔文半径(临界半径)仅为0.414 nm,直径为0.828 nm,远未达到IUPAC划分中孔的最低孔径2 nm,因而该点发生的数据点上漂不是中孔发生毛细凝聚引起.文献[18]指出数据点呈现非线性的原因为,实际微孔吸附剂并非如D-R方程假设的孔径均一,而是各个孔的孔径分布在一个区间内,导致了吸附过程中存在多段吸附(多段微孔填充).因此使用单个方程拟合描述一种微孔吸附剂的吸附过程并不准确.

(2)

式中:rk为开尔文半径,nm,rk反映在指定的相对压力(P/p0)下,能够发生毛细凝聚的最大吸附剂孔径.

1.4 本文提出的修正表达式

如1.3节所述,多个研究表明[8-10]在高相对压力区吸附数据点会出现明显上漂的情况,导致D-R方程在该部分拟合效果不佳.并且,现有文献中的DR数据图中数据点上漂呈现三个特征:(1)上漂的起点相对压力并不一致,在0.04~0.1之间变动;(2)上漂趋势均接近对数形式;(3)数据点的对数趋势上漂一直持续到相对压力最高的实验数据点.因此,为改善D-R方程在高相对压力区的拟合效果,本文提出了针对高相对压力区的D-R方程对数形式修正表达式,并对数据进行分段处理,使用D-R方程的修正表达式分别进行分段拟合.随后,本研究使用8~16目椰壳活性炭、4 mm柱状煤质活性炭、8~30目木质破碎炭这三种活性炭材料的试验数据对该修正表达式的准确性进行验证.

本文基于D-R方程提出的活性炭吸附特性的D-R修正表达式如下:

(3)

式中:b1、b2均为修正系数,根据实验数据拟合得到,与吸附剂种类有关.

需要指出,本研究使用的分段拟合的分界点为[ln(p0/P)]2=2.59和[ln(p0/P)]2=10.针对微孔活性炭吸附剂,这两个分界点为固定点,理由如下:

(1) 如1.3节所述,现有文献中吸附数据点的上漂分界点不完全一致,为提高本文提出的修正表达式的适用性,本文将修正表达式与原始D-R方程的第一个分界点定为[ln(p0/P)]2=10,该点对应的相对压力约为0.04.因此,使用该点作为分界点能够使修正表达式充分覆盖文献[8-10]中的上漂数据点.

(2) 需要指出,在将以[ln(p0/P)]2=10作为第一个分界点并不会导致修正表达式范围过大的问题,因为在自变量较大时,对数函数的自变量与应变量的关系接近线性,这使得本文提出的修正表达式在分界点附近的函数图像与原始D-R方程较为统一(本文第三节的验证部分可以体现).

(3) 本文将修正表达式的另一个分界点定为[ln(p0/P)]2=2.59,因为原始D-R方程限定了只能在相对压力低于0.2的情况下适用,该相对压力对应[ln(p0/P)]2=2.59.本研究为针对D-R方程在高相对压力下的修正,故本研究提出的修正表达式范围不超出原始D-R方程的适用范围.

2 测试材料与实验验证

本研究选取三种商业活性炭作为吸附剂,这三种活性炭分别为上海三山炭业科技有限公司生产的8~16目椰壳活性炭、4 mm柱状煤质活性炭、8~30目木质破碎炭.

本研究使用美国康塔仪器的Quantachrome Autosorb-1测试仪来测试三种实验样品的氮气吸脱附曲线.实验步骤如下:

(1) 脱气:样品装入样品管后,将样品管装在脱气口,在120 ℃加热下脱气12 h左右后取下.

(2) 测试:将样品管装在测试口,启动微孔测试程序(相对压力范围为10-5~1).在液氮温度(77.4 K)下,进行氮气吸附脱附测试,得到吸附脱附等温线.

测试得到这三种活性炭材料的吸脱附曲线后,本研究使用Horvath—Kawazoe method方法(HK方法)计算其孔径分布,并用t点法计算微孔比表面积[19-20].测得各活性炭特征参数对比如表1所示.由表1可见,本实验中使用的三种活性炭材料的微孔比例均高于95%,且集中分布孔径为0.6 nm左右,故这三种活性炭吸附材料均为微孔吸附材料,且理论上可使用D-R方程描述其吸附过程.

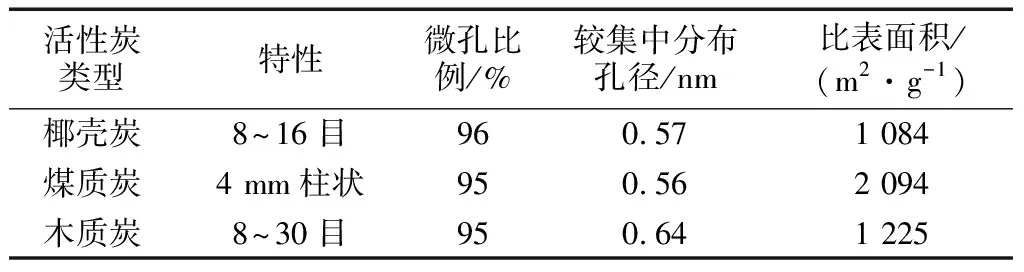
表1 各活性炭特征参数对比

3 数据拟合结果与讨论

3.1 拟合结果

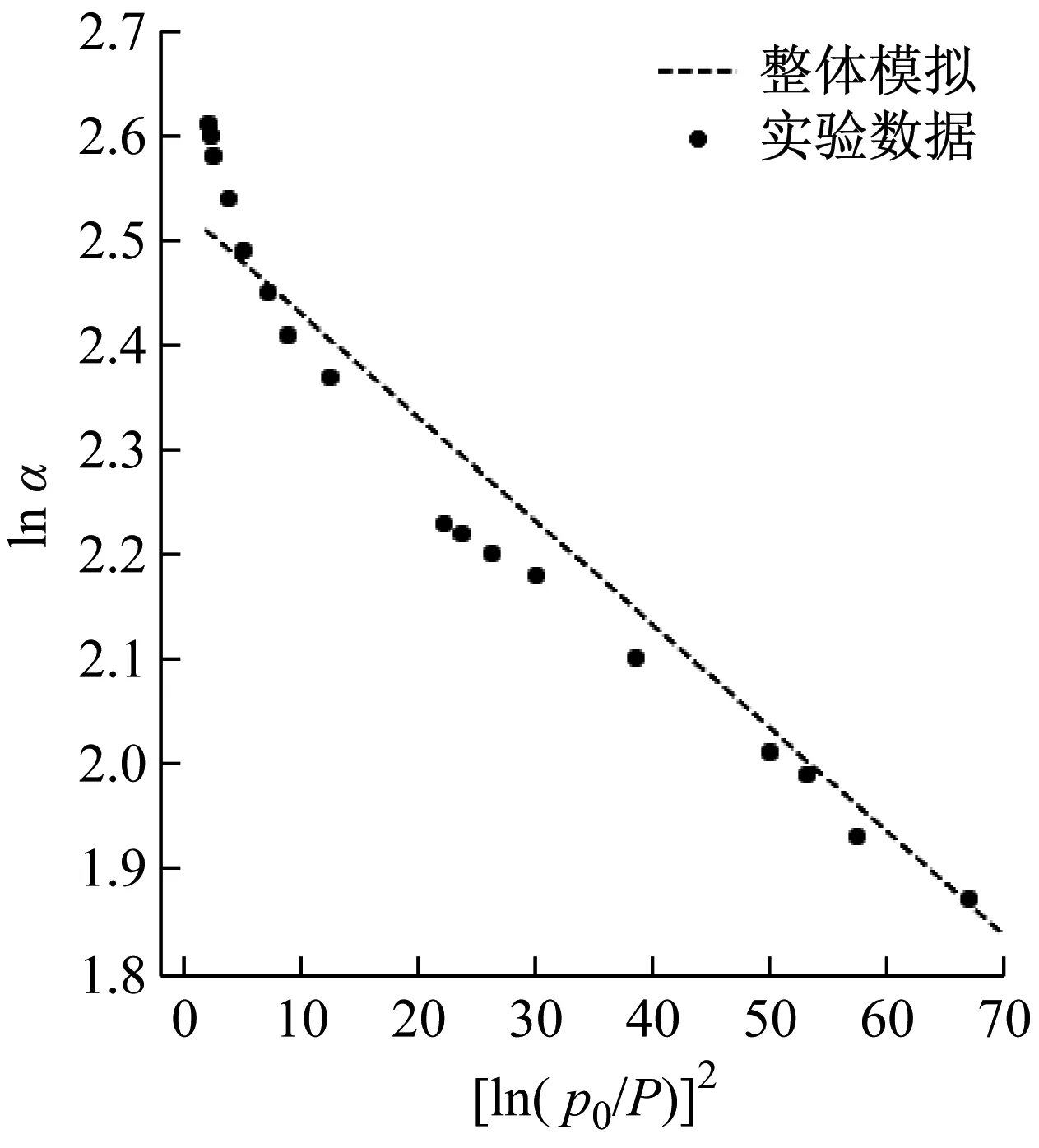
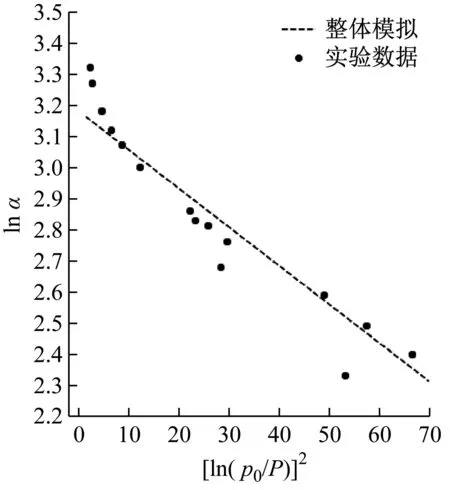
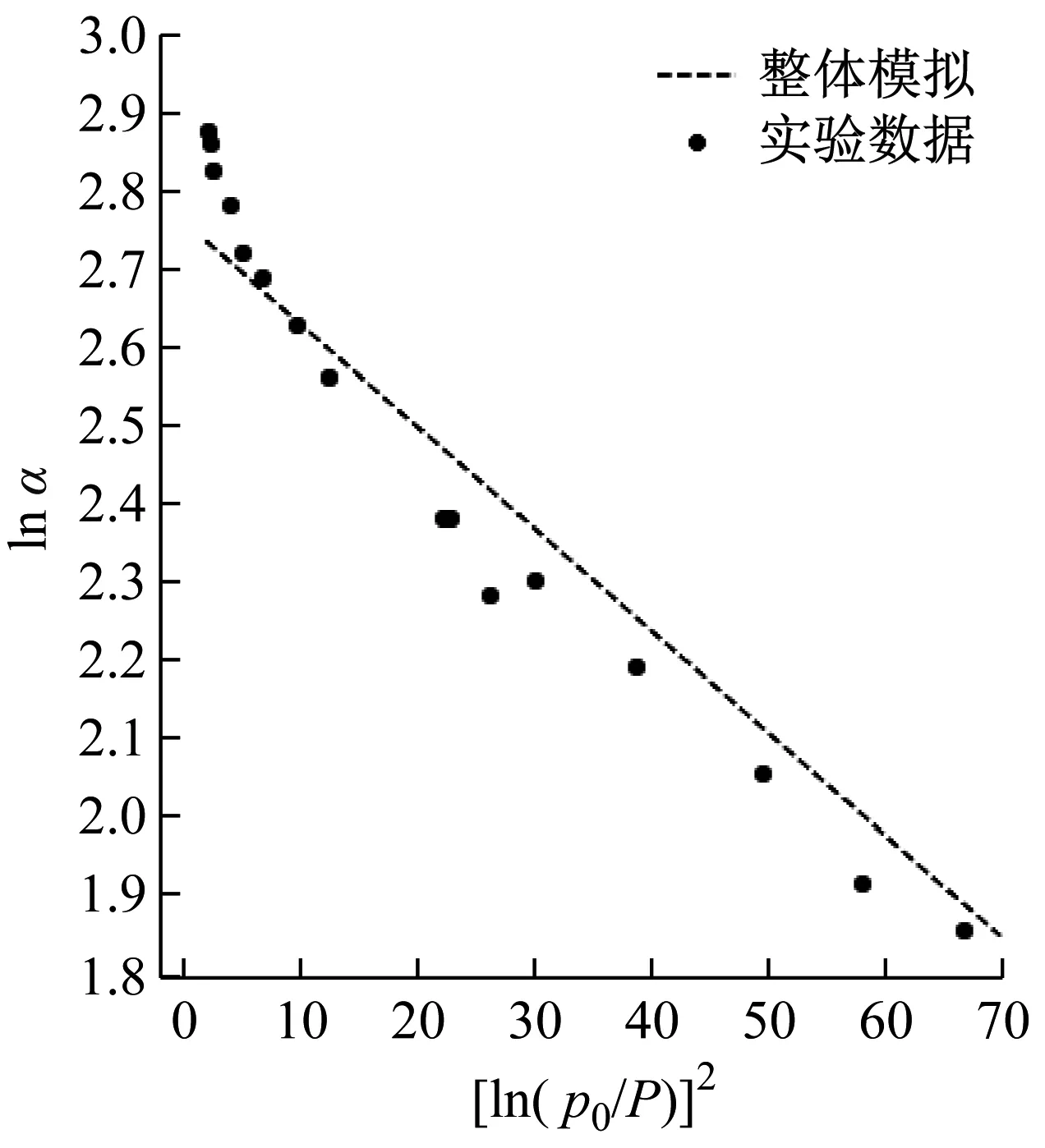
第2节的实验可以得出三种吸附材料的吸脱附曲线及吸附数据点.本节分别使用原始D-R方程整体拟合和修正表达式分段拟合两种方法对实验数据点进行拟合描述.分段拟合时,对2.59<[ln(p0/P)]2<10的数据点使用式(3)进行拟合,对 [ln(p0/P)]2>10的数据点使用式(1)进行拟合.整体拟合时,对[ln(p0/P)]2>2.59的所有数据点使用式(1)进行拟合.拟合得到的表达式结果被汇总至表2.

表2 三种活性炭拟合结果汇总

实验数据拟合结果如图1所示,可以看到,相比原始D-R方程整体拟合得到的直线,使用本文提出的D-R方程修正表达式分段拟合的曲线能更为准确地描述实验数据.

3.2 讨论

如3.1节中三种活性炭的整体拟合函数图(图1)所示,直接使用原始D-R方程整体拟合所有实验数据时,在2.59<[ln(p0/P)]2<10范围内明显欠拟合,而使用本文提出的修正表达式进行分段拟合后,拟合准确性得到提升.本研究使用拟合优度(R2)和均方根变异系数(CV,RM)两种指标[21-23]来分析对比整体和分段拟合结果的准确性,整理结果如表3所示.结果表明,对这三种活性炭吸附材料而言,分段拟合的精度均比整段拟合的精度高,即修正表达式能够更加准确地描述吸附特性.

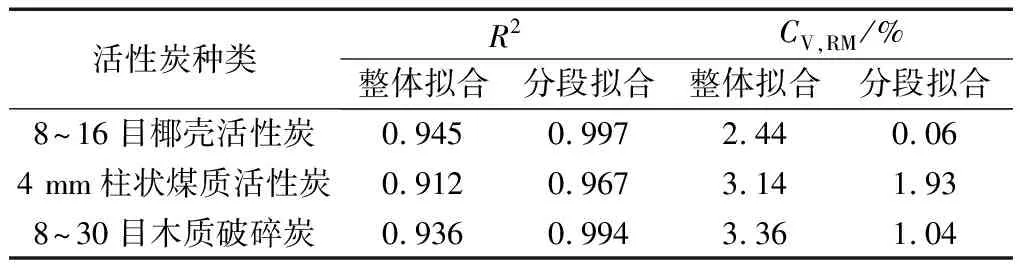
表3 三种活性炭的整体和分段拟合结果准确性比较

本研究认为使用修正表达式后拟合精度提升的原因是,D-R方程的其中一个假设为微孔吸附材料的微孔孔径均一,然而实际的微孔吸附材料的各个微孔的孔径是分布在一个区间内,因此该假设在实际情况中较难满足.实际的微孔吸附材料孔径不均一,则会导致微孔吸附过程包含多段吸附[18],因此使用原始D-R方程来描述整个吸附过程会出现精度下降的情况.本研究由实验数据出发,观察并考虑了该问题,依据数据点的漂移趋势提出了修正表达式,并用修正表达式来针对性描述DR图上非线性段的吸附过程,因此本研究提出的修正表达式可达到更优的拟合精度.

4 结论和展望

本文基于吸附特性曲线提出D-R方程修正表达式,该表达式使用对数函数描述2.59<[ln(p0/P)]2<10区间的活性炭吸附特性,使用原始D-R方程描述[ln(p0/P)]2>10的部分.为了验证该修正表达式,笔者分别对8~16目椰壳活性炭、4 mm柱状煤质活性炭及8~30目木质破碎炭三种活性炭吸附材料进行氮气吸脱附测试,拟合测试数据对修正表达式进行验证.通过计算拟合优度R2和均方根变异系数CV,RM两项指标可知,相比原始的D-R方程,本文提出的修正表达式针对这三种活性炭材料的拟合精度更高,因此,本文提出的方法可适用于工程插值计算.

致谢

感谢同济大学周斌教授课题组提供的实验设备与实验操作支持