方形截面高层建筑间气动干扰对其驰振稳定性的影响

全 涌, 陈宇辉, 车旭彬,2, 顾 明

(1. 同济大学 土木工程防灾国家重点实验室, 上海 200092; 2. 广东保利房地产开发有限公司, 广东 广州 510308)

随着技术的进步,为了更大的经济效益、社会效益和提高土地使用效率,建筑高度及高宽比不断增加,其刚度偏于更柔,质量偏于更轻,阻尼偏于更小,这使得其驰振稳定性问题逐渐凸显出来.驰振分析最早源于Lanchester描述的一种“空中陀飞轮"的现象[1].Den Hartog[2]针对输电导线在风作用下发生驰振的必要条件,提出了著名的Den-Hartog驰振判据.Novak等[3]对柱体的驰振进行了深入研究,发现准定常理论在三维湍流中也具有较高的准确性.此后不断有研究者对驰振的稳定性进行分析,顾明和项海帆[4]研究了斜拉桥塔的驰振稳定性,采用平均法求解驰振方程得出任意风速下幅值的各阶稳态解和结构的响应幅值.Yu等对覆冰导线采用Blevins提出的惯性耦合模型[5],给出了一次近似解并分析了其稳定性以及产生周期运动的条件[6].钟万勰[7]将精细时程积分法应用于高耸结构驰振临界风速的确定,并根据结构时程响应的对数衰减率来判断结构驰振临界状态.Kawai[8]通过风洞试验研究了风向角和湍流度对超高层建筑驰振的影响,发现当来流垂直于迎风面时涡激共振和驰振发生的临界风速最小,并且宽厚比对临界风速的影响较小.张相庭[9]则通过取实际结构第一阶振型来确定驰振的临界风速.罗兵[10]介绍了两种桥塔结构的驰振临界风速的计算分析方法,并结合工程实例及基于计算流体动力学(CFD)的桥塔截面的静力三分力系数模拟结果进行研究.

强风作用下结构物之间的气动干扰效应开始受到广泛关注是源于1965年英国西约克郡费里布里奇热电厂的两排8座冷却塔在风力作用下发生破坏.Armitt[11]认为是干扰效应增大了后排冷却塔受到的风荷载.Bailey和Kwok[12]研究发现干扰效应在开阔地貌条件下最严重.Blessmann和Riera[13]发现不同的湍流场中干扰效应最明显的施扰物的位置有所不同.Gowda和Sitheeq[14]采用流场显示的方法对干扰机理进行了研究,分析了串列布置的两个矩形建筑物情况.黄鹏[15]通过风洞试验研究了两个高层建筑间的风致干扰效应,分析了多种因素的影响.谢壮宁[16]采用刚性模型高频测力和扫描阀测压两种风洞试验详细地研究了两个和三个高层建筑间整体静力、动力干扰效应和结构典型位置处的风压系数在受扰后的变化.匡济[17]则通过数值模拟的方法对超高层建筑双塔结构的气动力特性及驰振响应进行了研究,并分析了各工况下的驰振临界风速.谢兰博[18]通过试验和CFD分析,提出了有风向角的驰振计算方法和驰振振幅的能量分析方法.

尽管高层建筑驰振稳定性和干扰效应都得到了较为广泛深入的研究,但仍然存在一些问题.高层建筑驰振稳定性的研究多集中于来流方向垂直于振动方向的情况,对来流方向与驰振方向非正交的情况研究较少.建筑结构间气动干扰效应的研究一般着眼于流场、气动力、气动响应等方面,尚未见到关于干扰效应对驰振稳定性影响的研究.

本文通过刚性模型高频天平测力风洞试验,对任意风向下方形截面超高层建筑的驰振力系数和驰振临界风速及临近建筑的干扰效应进行了研究.

1 任意风向下的驰振力系数和驰振临界风速计算理论

谢兰博推导了风轴坐标系和体轴坐标系下任意风向的驰振运动方程[18],本文通过建立广义坐标系,将其体轴坐标系的驰振分析理论用于高层建筑的基阶模态振动.如图1所示,将直角坐标系原点建立在超高层建筑底部中心,高度方向为z轴,关注的侧弯振动的振动方向为y轴,x轴与y轴正交,来流与x轴的夹角为α0,结构顶部高度处H的来流风速为vH,结构顶部位移为y.

图1 结构风向角及坐标系示意图

将广义坐标设置于结构物顶部,并将该结构的一阶侧弯模态振型简化为线性函数φ1(z)=zH-1,同时认为结构物质量密度均匀分布,则谢兰博体轴坐标系的驰振运动方程[18]可改写为

(1)

式中:ζ1为结构阻尼比;f1为结构一阶频率;ρa为空气密度;ρs为建筑物密度;B为建筑物特征宽度;CFy(α0)为α0风向角下作用在结构y轴上的广义气动力系数;Gal为驰振力系数,可用式(2)表示

(2)

由式(1)知,当总阻尼等于0,即4πζ1f1+3ρavcrGal(2ρsB)-1=0时,为驰振发生的临界条件.因此可得驰振临界风速νcr为

(3)

而式(1)中阻尼项内由于气动力而产生的气动阻尼比为

(4)

2 试验概况

试验在同济大学土木工程防灾国家重点实验室风洞试验室TJ-1边界层风洞中完成.风洞试验段高1.8 m,宽1.8 m,长12 m,最大试验风速为30 m·s-1.根据研究的需要,采用尖劈,格栅和粗糙元以被动模拟方法模拟了不同湍流度的四类(Ⅰ~Ⅳ)风场,模型顶部高度处(0.6 m)的湍流度分别为0,5%,10%和15%,平均风速剖面和湍流度剖面如图2所示.图中,Uz为z高度处风速,UH为建筑高度处风速,z为纵坐标高度,ZH为建筑物高度.

a I类风场

b Ⅱ类风场

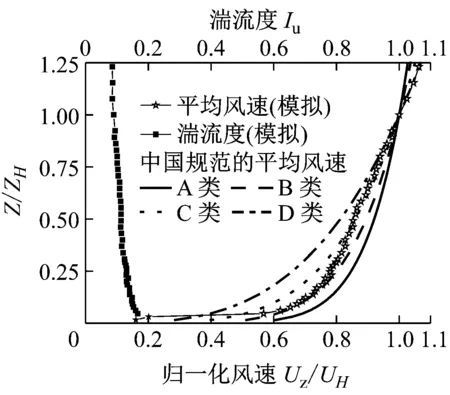
c Ⅲ类风场

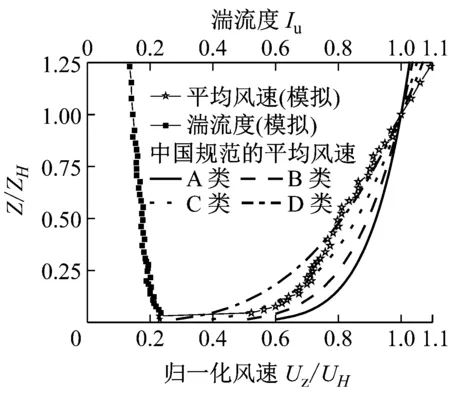
d Ⅳ类风场

试验制作了两个高宽比均为9,高宽厚分别为630 mm×70 mm×70 mm的方形截面超高层建筑模型.试验模型由截面宽度为50 mm,壁厚为1 mm的铝合金方管芯棒来提供刚度,在铝棒外部包裹航空木板提供光滑表面.模型与天平组成的系统的频率在60 Hz左右,大约是所关心的气动力卓越频率的3倍左右.试验风向角取以下角度:-90°~-60°以及60°~90°间隔15°,-45°~-25°以及25°~45°间隔5°,-20°~20°间隔2°,共有37个风向角.图3为本文试验的干扰建筑模型的移动网格和坐标系.设定建筑物宽度为b,干扰建筑的位置用[X,Y]坐标描述,X在(0~8b),Y在(-4b~10b)范围变化.有36个试验干扰位置,涵盖正前方,侧前方,侧后方等多个位置,在4种风场中共有148种工况.

3 试验结果

基于风洞试验得到的建筑各风向角下的基阶模态广义气动力系数均值CFx和CFy,通过式(2)计算得到驰振力系数.由式(3)可知,只有当驰振力系数为负的时候才有发生驰振的可能,且驰振力系数越小(负值的绝对值越大),发生驰振的临界风速越小,意味着驰振发生可能性越大,驰振的不稳定性越强.

3.1 孤立工况

图4给出了孤立工况下目标建筑的驰振力系数随来流湍流度和风向角的变化情况.图中,IH为H高度处的湍流度.由于孤立工况下流场和模型都是轴对称的,驰振力系数也是关于0°风向角对称的,因此这里只给出了风向角为正值的结果.

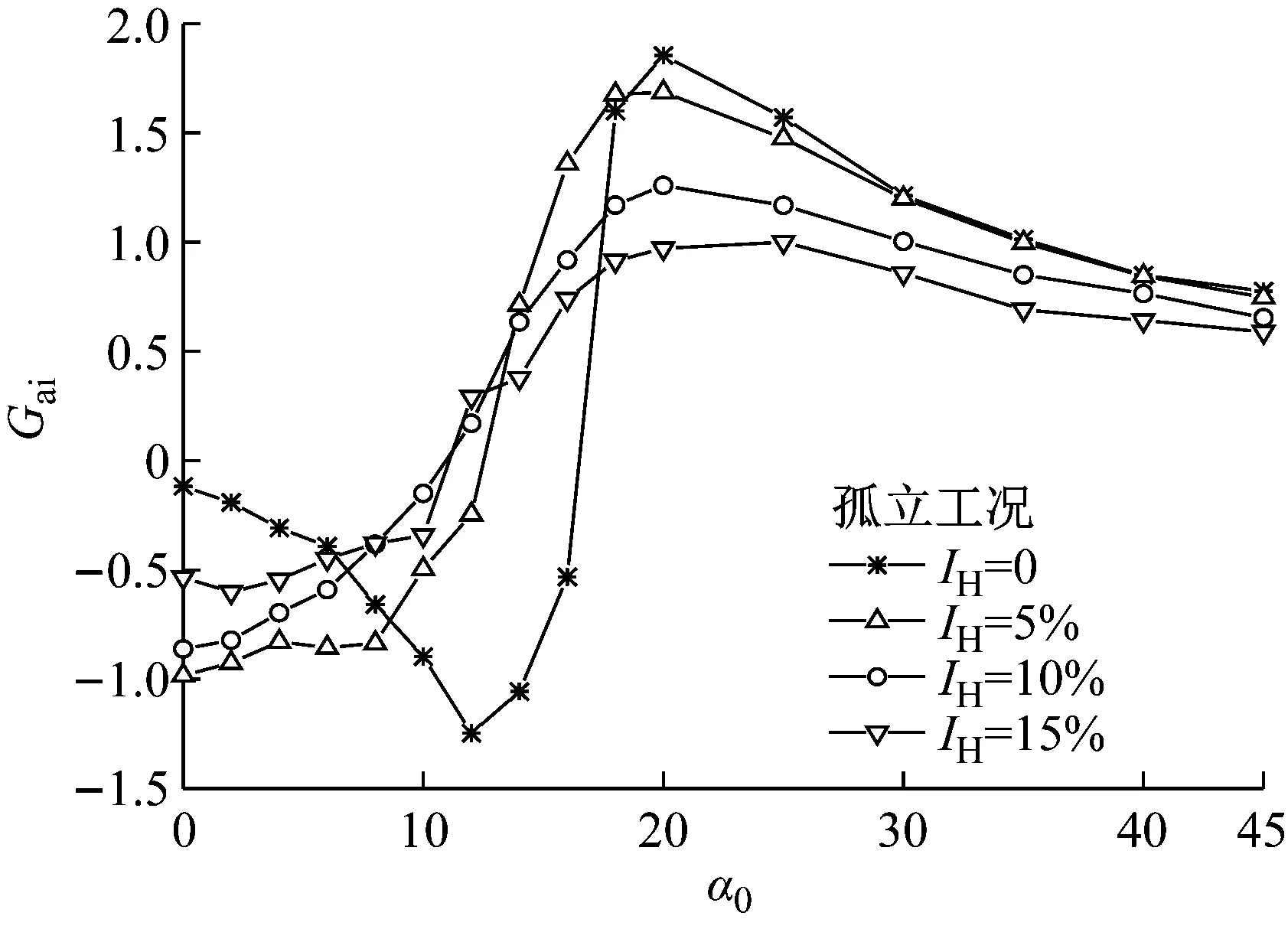
图4 独立工况驰振力系数随风向角变化曲线

Fig.4 Curve of the variation coefficient of the independent working condition with the wind direction angle

当湍流度为0时,只有在0°~16°风向角范围内驰振力系数才为负值.当风向角等于0°,即来流方向正对建筑体轴时,Gal=-0.117,尽管是负值,但绝对值很小,并不容易发生驰振.当风向角从0°逐渐增大到12°的过程中,Gal的绝对值逐渐增大,并在风向角为12°时达到了峰值-1.25.也就是说,在湍流度为0的风场中,方柱在12°斜风作用下最容易发生驰振.当风向角大于12°后,随着风向角的进一步增大,Gal的绝对值迅速减小,并在17°左右的时候变成正值,驰振不再可能发生.

湍流度不为0的三个工况中驰振力系数Gal呈现出不同于湍流度为0时的规律性.当湍流度不为0时,驰振力系数在风向角0°~12°区间时才出现负值.在该区间内,不同于湍流度为0的工况,驰振力系数最大绝对值发生在0°风向角处,即来流方向与建筑体轴一致时最容易发生驰振,在该风向工况下,三个湍流风场工况中湍流度较小(5%)的工况中驰振力系数Gal的绝对值最大,达到-0.98.随湍流度的增大,Gal绝对值逐渐减小,在湍流度达到10%时,Gal绝对值减小到-0.86,湍流度达到15%时,Gal绝对值减小到-0.53.随着风向角的逐渐增大,湍流风场工况中Gal绝对值逐渐减小,直到风向角增大到12°左右时,Gal变成正值.

总的说来,对于孤立方柱而言,在无湍流风场中,12°斜风工况发生驰振的可能性最大.在湍流风场中,0°风向角(即风向与建筑体轴一致)时发生驰振的可能性最大,且小湍流风场下更容易发生驰振.

3.2 干扰工况

通过3.1节的分析可知,驰振力系数仅在一定的区间内为负值,且在0°风向角时取到最小值.为了更加清晰地展示干扰效应对驰振力系数的影响,将各干扰位置的驰振力系数在0°风向角时的值绘制成等值线图,如图5所示(图中原点处方块代表受扰建筑物).图中坐标代表了干扰建筑所在位置,而等高线值则代表驰振力系数在0°风向角时的值.当湍流度为5%时,Gal最小值为-0.98,当湍流度为10%时,Gal最小值为-0.86.

a 湍流度为5%

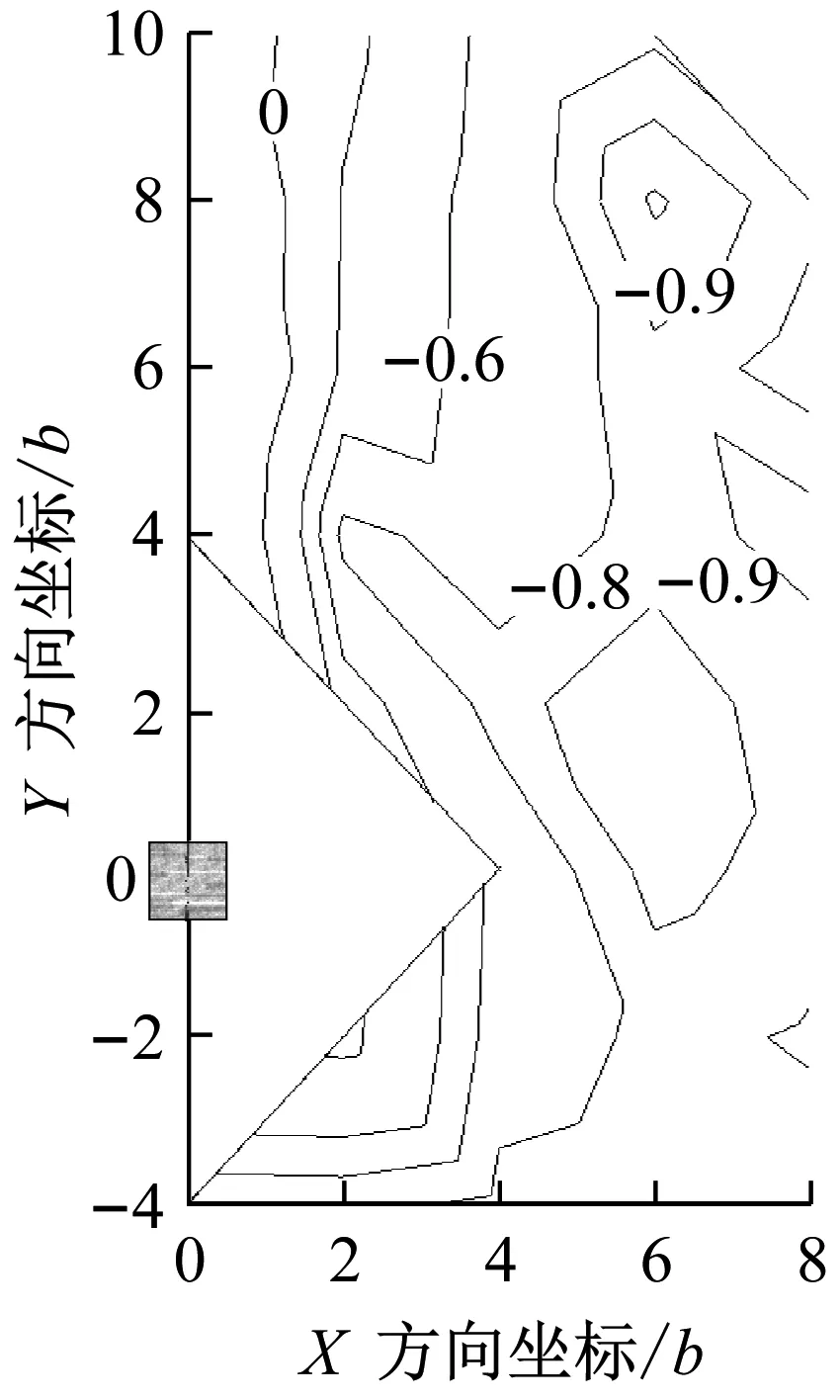
b 湍流度为10%

Fig.5 Contour map of the turbulence coefficient of each turbulent flow at 0° wind direction angle

当湍流度为5%和10%时,在大部分干扰位置(特别是当干扰建筑位于目标建筑上游时),驰振力系数都大于相应湍流度下孤立状况下的最小值,说明邻近建筑的出现会使目标建筑更不容易发生气动失稳.仅有5%湍流度工况下的坐标位置(4b,-2b)、(6b,0)附近、10%湍流度工况下的坐标位置(6b,8b)、(6b,2b)及(8b,4b)附近的驰振力系数比孤立工况更小,导致目标建筑更容易发生驰振失稳.总而言之,在有湍流工况下,干扰建筑位于绝大部分区域时,驰振稳定性都有所增加,但仍有少部分区域目标建筑的驰振稳定性会减小.

4 结论

本文通过刚性模型高频天平测力风洞试验,在4种模拟风场中,分析得到37个风向下的方形截面超高层建筑的驰振力系数,得到如下结论:

(1) 孤立方形截面超高层建筑,在无湍流风场中,风向与结构体轴的夹角为12°时的驰振稳定性最差;而在湍流风场中,风向角在0°附近时驰振发生的可能性最大,且湍流度或风向角增加,驰振发生的可能性都会逐渐减小.

(2) 在湍流度为5%、10%的风场中,同外形的邻近建筑在大部分位置时,目标建筑在0°风向角附近的驰振稳定性都有所增加,仅在少部分干扰位置出现时会使目标建筑在0°风向角附近的驰振稳定性降低.