肌音信号典型时域、频域特征与肌力关系研究

华东理工大学机械与动力工程学院（上海200237）

有关肌肉输出力的研究在骨骼服[1]、康复机器人[2]、假肢控制[3]以及与肌肉相关的疾病研究[4]等领域均有广泛应用，因此了解肌力与生物医学信号特征之间的关系具有十分重要的意义。目前已有研究者研究了生物医学信号与肌力之间的关系，其中主要为表面肌电信号（surface electromyography，sEMG）与肌音信号（mechanomyogram，MMG）。相比于MMG，sEMG研究起步较早，吴小鹰等[5]分析了sEMG的幅值与握力之间的相关性，证明了sEMG幅值随肌力的增大而线性升高。于在洋等[6]进一步分析了sEMG的复杂度与肌力之间的关系，使用线性模型和指数模型分别对其进行拟合，结果表明二者更符合指数关系。黄耐寒等[7]的研究则认为肌力与sEMG的均方根值（root mean square，RMS）之间符合二次多项式关系。在MMG特征与肌力的关系研究中，Akataki等[8]发现随着肱二头肌肌力线性上升，MMG的RMS值先上升后下降；而Beck等[9]对肱二头肌的研究却发现肌力与MMG的RMS值呈现良好的线性关系。以上研究结果说明，不论sEMG还是MMG，其特征与肌力之间的关系模型尚无明确统一的结论，值得进一步深入研究。有研究显示，同时使用MMG与sEMG预测肌力的效果优于单独使用sEMG[10]，但这增加了采集与分析的复杂度。MMG是在肌肉收缩时由肌纤维横向振动产生，可以反映肌肉收缩时力学特性的一种低频信号。与sEMG相比，MMG的采集操作方便，传感器的定位要求较低，并且即使在运动肌肉末端仍可被采集到。基于以上优点，本研究试图单独使用MMG来研究其特征与肌力之间的关系，并通过对比分析找到最优的统一的关系模型。现有的基于MMG特征的肌力研究[11-13]大多采用黑箱模型，这种模型无法直观表达MMG与肌力之间的内在联系[14]，而参数化模型可以明确表达出MMG特征与肌力之间的函数关系，因此本研究探讨肌力与MMG特征之间的参数化模型。

本研究以健康受试者的肱三头肌为研究对象，主要目的是研究MMG特征与肌力之间关系的参数化模型。在提取积分肌音值（integral mechanomyogram，IMMG）与频谱均方根值（frequency spectrum root mean square，FSrms）分别作为MMG的时域和频域特征的基础上，使用双因素一元方差分析方法证明这两种特征随肌力发生显著变化。随后使用线性、二次多项式以及指数等三种参数化回归模型分析肌力与MMG特征之间的关系，并采用假设t检验比较三种模型拟合优度的差异显著性，最终得到最优的参数化模型。

1 实验方法

选取肱三头肌为研究对象，选用TD-3加速度传感器采集MMG，传感器放置在肱三头肌的肌腹位置，使用弹力带进行固定。选用ZNLBS-VI-30KG拉压力传感器和ZNBSQ-V模拟变送器采集手部输出力信号。通过NI公司的9205数据采集卡对MMG与肌力信号进行同步采集（采样频率为1000Hz）以及A/D转换后传输到PC平台。

本实验共招募10名男性志愿者（年龄22～25周岁，体重56～80 kg），均无运动神经类疾病史，上肢未出现过运动损伤状况，且实验前两天内未进行过剧烈运动，没有肌肉酸痛及不适等症状。在明确实验过程并签署知情同意书后进行实验。

实验过程中要求受试者坐在防滑椅上，上半身保持直立姿势，大臂与身体夹角为90°，小臂与大臂之间夹角为90°，发力过程中避免身体晃动，如图1所示。

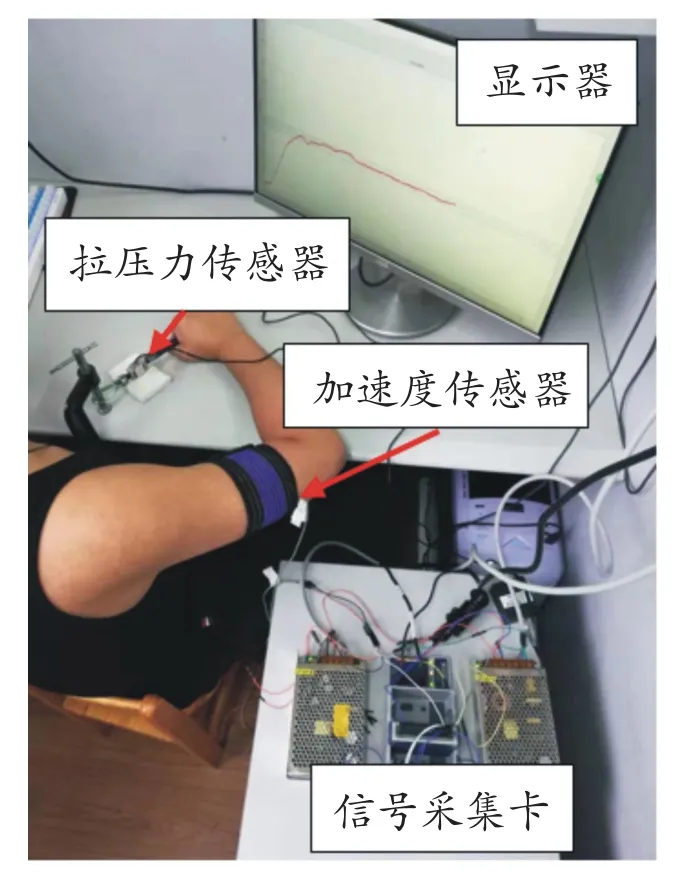
图1 实验装置

实验分两步进行：（1）测量受试者的最大自主收缩力（maximal voluntary contraction，MVC），将其作为衡量力大小的标准。为避免瞬间爆发力，要求受试者缓慢施力，直至力不能再上升为止；本过程重复3次，相邻测试之间受试者进行充分休息，取3次所达最大力的平均值作为最终MVC。（2）采集受试者在不同发力等级下的MMG，发力等级设置为10%～100%MVC，梯度为10%MVC，不同发力等级随机进行，为避免肌肉疲劳，相邻两次测试间休息2分钟。受试者被要求维持每个发力等级至少5 s，其面前的显示器会显示肌力目标曲线与实测曲线，为受试者提供视觉反馈，以便维持稳定发力。10名受试者的MVC如表1所示。

表1 10名受试者的MVC（kg）

2 数据处理

2.1 数据选取及预处理

对于每个发力等级的信号，设置误差区间为±3%MVC，根据力曲线选择其中发力稳定性较好的3 s区间，并选取与其对应的MMG进行分析，如图2所示。

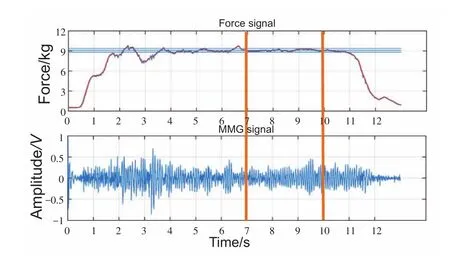
图2 数据选取

MMG的有效频段集中在5～60 Hz的频率范围，因此本研究使用5～100 Hz的带通滤波器对原始信号进行滤波处理。

2.2 特征提取

在以往有关MMG的研究中，使用的时域特征包括RMS、方差（variance，VAR）、绝对平均幅值（mean absolute value，MAV）等;频域特征包括中值频率（median frequency，MF）、平均功率频率（mean power frequency，MPF）等。本研究通过比较10名受试者MMG的时域、频域特征发现，许多特征随肌力变化的趋势相似，而IMMG与FSrms在诸多的特征中随肌力变化得比较明显，且个体间差异较小，因此本研究提取IMMG和FSrms分别作为MMG时域和频域特征。

IMMG表示单位时间内MMG波形曲线下面积的总和，其计算公式如下：

（1）式中，Si为MMG在第i个数据点处的幅值，n为信号数据点个数。

FSrms是对信号的时-频谱计算RMS得到的，通过小波变换得到MMG的时-频谱，其计算公式为：

（2）式中，t为时间，f为频率，cwt（t，f）为小波变换，S（t，f）为变换后得到的时-频谱。

将求得的S（t，f）代入式（3）计算FSrms值：

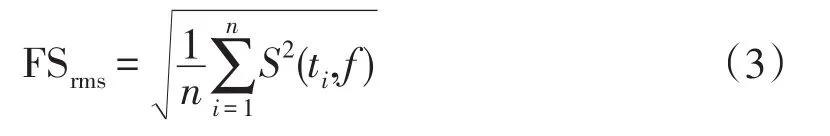
计算得1名受试者的IMMG、FSrms随肌力变化的情况如图3所示。

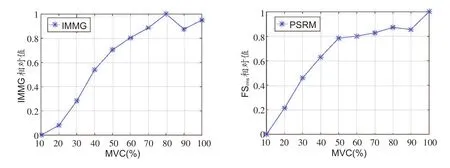
图31 名受试者IMMG（左）、FSrms（右）随肌力变化情况

对10名受试者的MMG提取IMMG与FSrms，进行归一化处理后所得不同肌力下两种特征的平均值如图4所示。

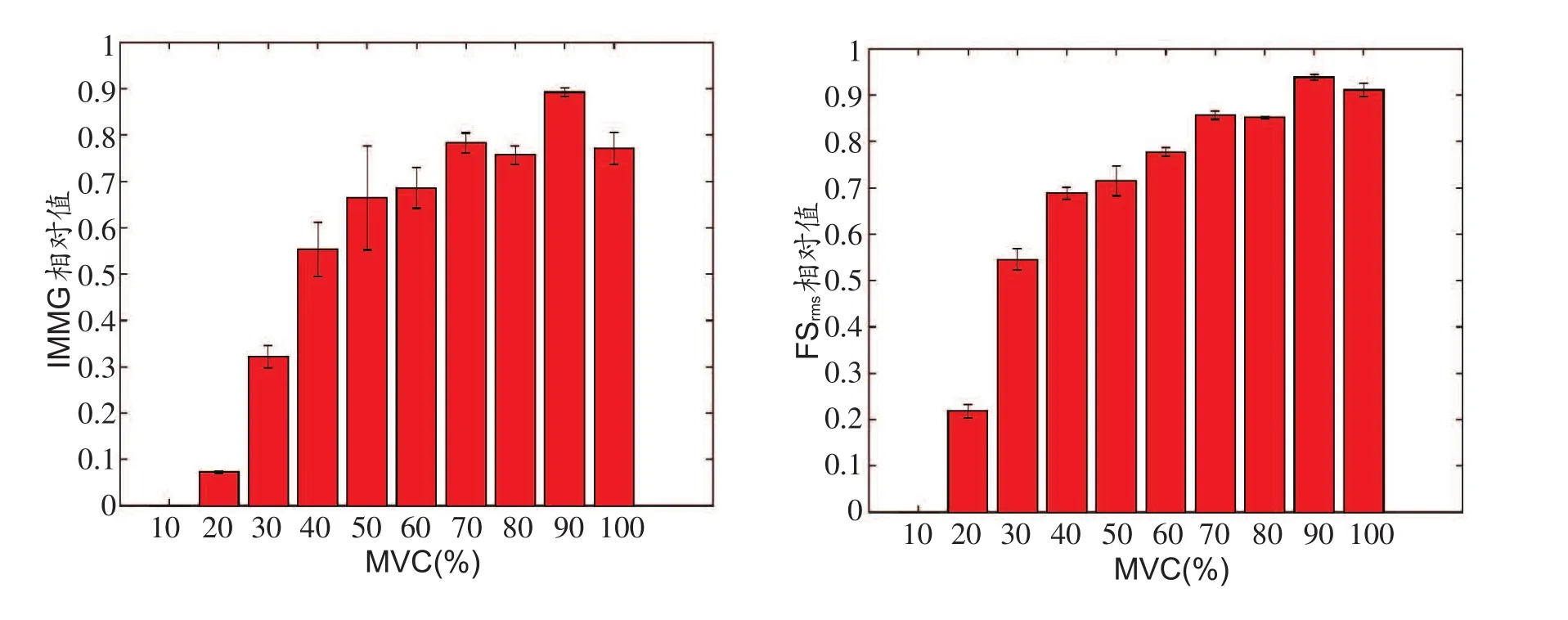
图410 名受试者IMMG（左）、FSrms（右）随肌力变化趋势

从图4可以看出，两种特征均会随肌力发生规律性变化。为说明特征随肌力变化的显著性，本研究采用双因素一元方差分析的方法对这两种特征随肌力变化的显著性进行验证。以序号为1的受试者的IMMG为例，首先将同一肌力下的MMG平均分为10段，对每段分别提取IMMG，共得到100个特征值（10个肌力等级X每个肌力等级的10段MMG），同一肌力下的特征值处于同一行内，构成10X10的特征值矩阵X。假设肌力因素为影响因子A，同一肌力下导致特征值变化的其他因素为影响因子B。现假设因子A与因子B对矩阵的影响均不显著，取α=0.05，则统计量F的计算过程如下：

计算各个离差平方和：

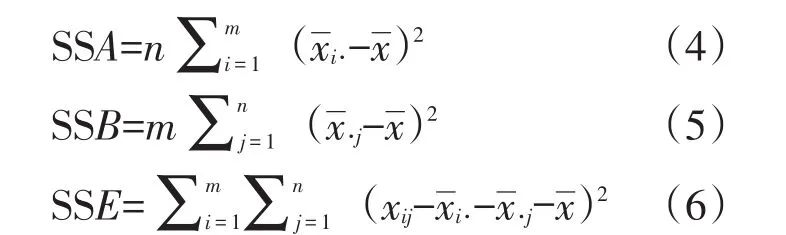
（4）、（5）、（6）式中，SSA、SSB分别为因子A、B的偏差平方和，SSE为误差平方和，m和n分别为矩阵X的行数和列数，xi·表示矩阵 X第i行的平均值，x·j表示矩阵X第j列的平均值。

统计量F的计算公式如下：

（7）、（8）式中，MSA、MSB、MSE、分别表示因子A、因子B以及误差的均方差，MSA=SSA/（m-1），MSB、SSB/（n-1），MSE=SSE/[（m-1）·（n-1）]。

通过查找F分布表计算Fα＞F的最小显著性概率P，计算结果如表2所示。可见因子B的最小显著性概率为0.5635，大于α=0.05，故接受原假设；因子A的最小显著概率为1.34×10-27，小于α=0.05，故拒绝原假设。即对于受试者1，相比于同一肌力下IMMG的变化程度，不同肌力下的IMMG变化更为显著。

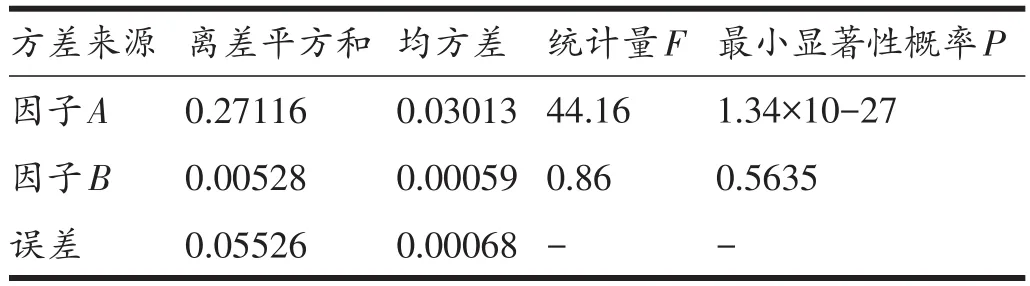
表2 方差分析计算结果

对10名受试者两种特征进行方差分析的P值计算结果如表3所示。从表3可以看出，肌力因子的显著性概率P均小于0.05，即IMMG、FSrms随肌力的不同而显著变化。

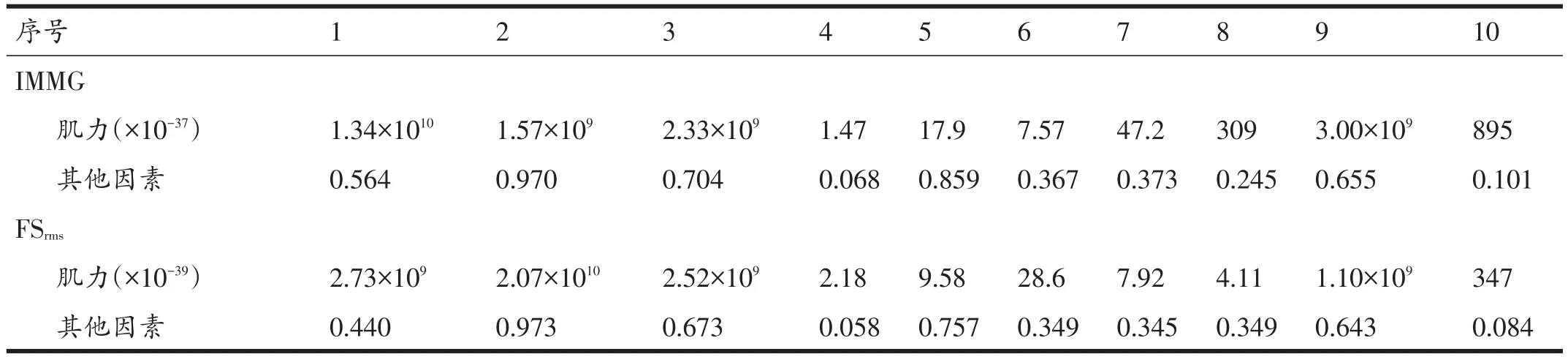
表3 肌力与其他因素方差分析的P值

2.3 曲线拟合

以往有关肌力预测的研究中通常采用黑箱模型，然而这种预测方法无法深入了解MMG与肌力之间的内在联系，难以反映普遍规律。因此，本研究选用参数化模型探索IMMG、FSrms与肌力之间的关系。以往的研究报道过MMG特征随肌力非线性上升的结论[8]，也有研究使用线性模型描述MMG特征与肌力之间的关系[9]。鉴于以上研究结果的争议，本研究同时使用线性模型y=a·x+b，二次多项式模型y=a·x2+b，以及指数模型y=xa·e（b-c·x）+d对MMG 的两种特征与肌力之间的关系进行拟合。图5为同一受试者两种特征与肌力的线性拟合、二次多项式拟合以及指数拟合曲线。

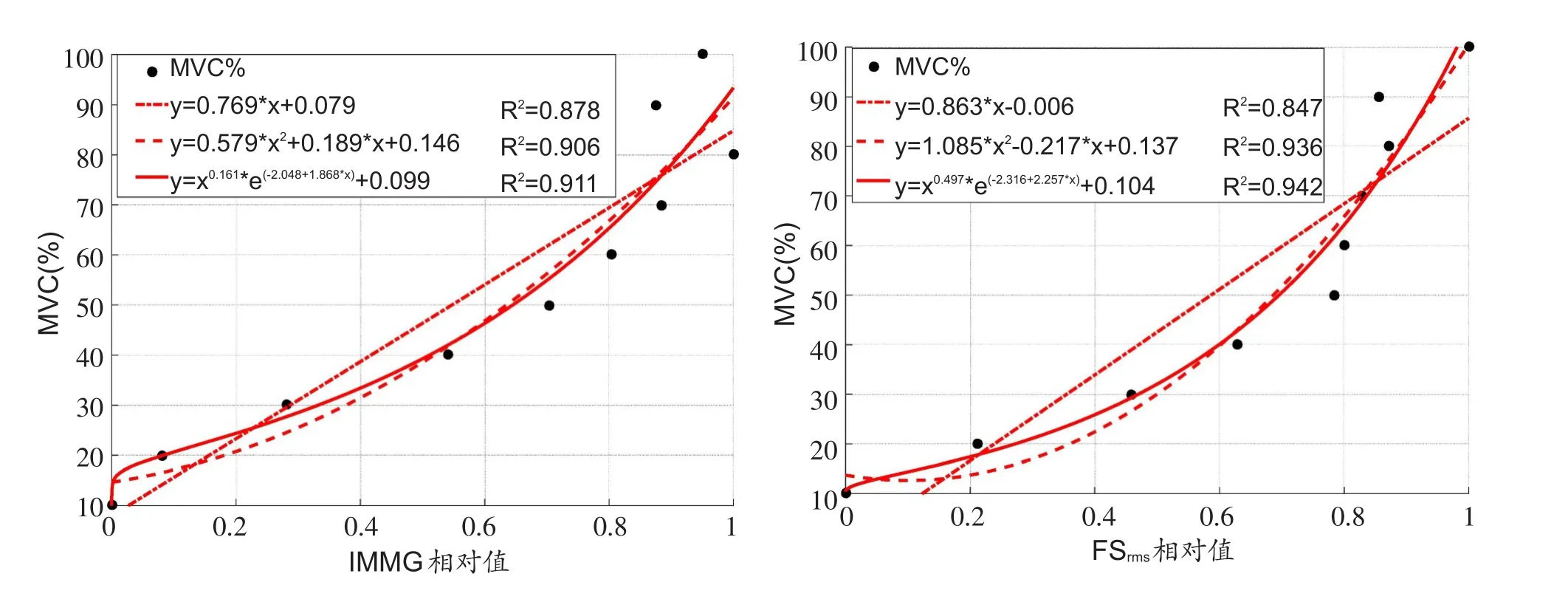
图5 某位受试者IMMG（左）、FSrms（右）与肌力的拟合曲线

为确定MMG的两种特征与肌力之间更符合何种函数关系，本研究采用拟合优度R2来评估拟合效果，计算10名受试者IMMG、FSrms与肌力的3种拟合方式的平均拟合优度，如图6所示。

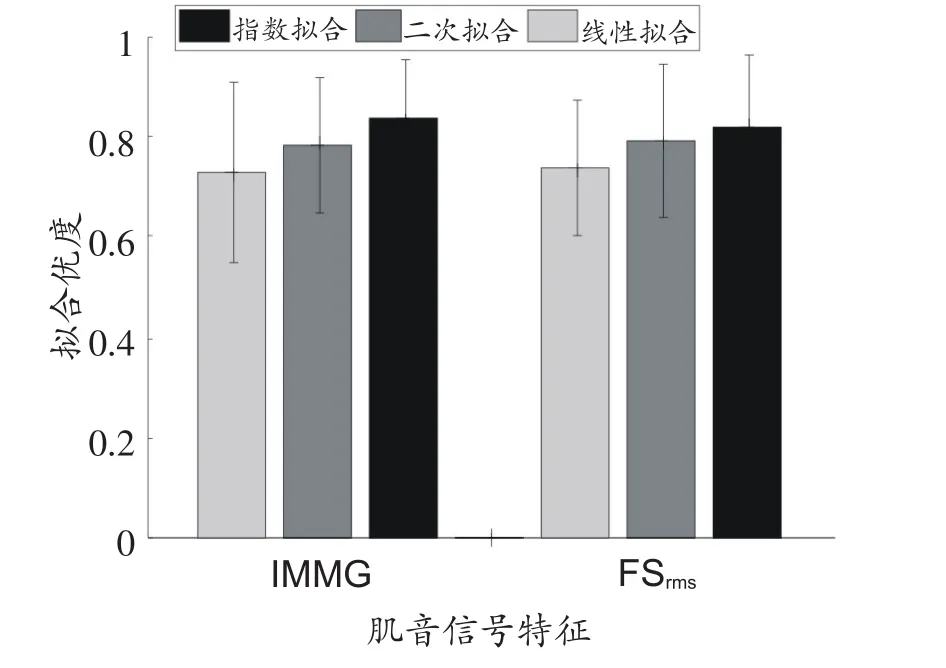
图6 10名受试者两种特征值与肌力的3种拟合关系的拟合优度

由图6可见，两种特征与肌力之间的关系更符合指数函数关系，而线性拟合的效果最差。为比较3种拟合方式之间差异的显著性，本研究采用假设检验中的成对数据t检验比较3种拟合方法的拟合优度之间是否具有显著差异。首先计算每两种拟合方法拟合优度的差值，由于对不同人的同一特征进行不同拟合方法获得的拟合优度之间的差值相互独立，故可认为每种特征的每两种拟合方式的拟合优度差值服从正态分布。以IMMG与肌力之间的线性拟合优度与指数拟合优度的比较为例，采用单边t检验的方法，现提出假设：

H0:μA-B=0，H1：μA-B＞0

其中，A表示指数拟合，B表示线性拟合，C表示二次多项式拟合，A-B即为指数拟合的拟合优度与线性拟合的拟合优度之差，下同。

统计量t计算如下：

（9）式中，X为指数拟合优度与线性拟合优度差值构成的向量，Xˉ为X的均值，s为X的标准差，n为X包含的样本数。

假设H0成立，即μA-B，故统计量t'为：

代入数据计算得t'=2.2562，查t分布上侧分位数表得t0.05（v）=1.833（其中自由度v=n-1，此处n-10），由t'＞t0.05（v）可知小概率事件发生，即原假设H1成立，表明在IMMG与肌力关系中，指数拟合优于线性拟合具有显著性。每两种拟合方法拟合优度差值的t值计算结果如表4所示。

表4 不同拟合方式拟合优度差值的统计量t

由表4可知，对于IMMG与肌力的拟合关系，二次多项式与指数拟合均显著优于线性拟合，并且二者间无显著差异；对于FSrms与肌力的拟合关系，指数拟合效果最好，二次多项式拟合效果次之，而线性拟合效果最差。

3 讨论

本研究以肱三头肌为研究对象，分析了MMG的时域特征IMMG、频域特征FSrms与肌力之间的关系。结果发现，IMMG与FSrms均会随着肌力变化，但即使在同一肌力下，这两种特征也会发生波动。本研究使用双因素方差分析证明了相对于同一肌力下的特征值波动，不同肌力间的特征值变化显著，故可以忽略同一肌力下的特征值波动。有研究表明，肌肉疲劳会引起同一肌力下的特征值变化[7]，因此在发力过程中，产生的肌肉疲劳可能是特征产生波动的原因之一。本研究中各受试者每次发力持续时间较短，而长时间发力造成的肌肉疲劳会导致何种结果还有待进一步研究。

IMMG与FSrms的总体趋势随着肌力的增大而增大，其中IMMG特征在10%～50%MVC阶段增长较快，在50%～70%MVC阶段增长缓慢，在80%MVC时出现第1次下降，随后在90%MVC时再次上升，在100%MVC时再次下降。对于MMG的FSrms特征值，其在10%～40%MVC阶段增长较快，随后在40%～70%MVC阶段增长较为缓慢，80%MVC时的FSrms值与70%MVC时几乎没有变化，随后同IMMG特征值变化趋势一样，在90%MVC时上升，在100%MVC时下降。对于参与实验的个体而言，IMMG、FSrms随肌力的变化趋势相似，有2例表现为上升后下降再上升的趋势，其余8例表现为上升后下降的趋势。本研究发现的MMG特征值随肌力增大而先升高后下降的趋势与以往研究[15-17]得到的结果一致。Akataki等[8]认为不同肌肉的MMG特征最大值对应的肌力不同，而且其研究发现肱二头肌在60%MVC后下降，股四头肌在70%MVC后下降。但也有研究[18]发现股四头肌在50%MVC后下降，由此可见实验个体对研究结果具有一定的影响，即存在个体间差异。

MMG是由肌肉收缩时肌纤维的横向振动产生的，在肌力逐渐增加的过程中，神经募集的肌肉单元发生变化，肌肉纤维的横向振动剧烈程度将会随之改变，因此MMG与肌力之间必然存在相关关系[18]。MMG特征值随肌力的升高而先升高后下降的现象可能是由肌肉运动单元的募集与肌纤维的尺寸变化所引起的[19]。随着肌力的增加，神经募集的肌肉运动单元越来越多，MMG特征值上升，当肌力达到90%MVC（此值因肌肉不同而不同）时，可募集的肌肉运动单元达到上限，肌力的增加主要来源于激活的肌肉运动单元激发率的增加，从而导致肌肉纤维尺度急剧变化，使得肌纤维横向振动减少，所以MMG特征出现下降趋势。另一方面也有研究发现传感器的压力大小也可能是导致MMG特征出现下降的原因[20]。因此，MMG特征在高肌力出现下降的原因有待进一步研究。

4 总结

本研究建立了MMG的时域、频域典型特征IMMG、FSrms与肌力之间的关系模型，方差分析的验证结果表明上述特征与肌力之间具有显著性关系。根据单边t检验的结果，指数模型相比于线性模型或二次多项式模型，对于上述特征与肌力之间的关系表现出了更高的拟合程度，拟合优度分别达到0.836±0.167与0.829±0.132，故IMMG或FSrms与肌力之间更符合指数关系。本研究可为MMG用于临床医学与康复工程等领域的肌力分析提供一种有效方法，为肌力预测研究提供依据。