考虑低碳的高维多目标柔性作业车间调度

黄夏宝，魏淑玲

(1.福建江夏学院 工商管理学院，福建 福州 350108；2.福州大学 经济与管理学院，福建 福州 350116)

随着全球经济的高速发展，能源消耗迅速、环境污染严重等问题日益突出，如何实现节能减排、减少环境污染成为当下亟需解决的重要问题之一。制造业产生了全球近1/3的能源消耗,制造过程中能源的大量消耗和CO2的过度排放对环境造成严重影响。因此，减少制造过程中的能量消耗，实现低碳的绿色制造是新时代下制造业的发展要求[1]。

在柔性作业车间中，允许工件的工序在不同的机器上加工，更符合现代制造车间的实际情况。同时，由于柔性作业车间调度问题(flexible job-sop scheduling problem, FJSP)是NP-hard问题，众多学者已对此问题展开了深入研究。单目标FJSP仅关注车间调度中单个性能指标的优化。LI等[2]以最大完工时间最小为目标，将遗传算法局部搜索方法相结合，综合提升算法的搜索能力。SOBEYKO等[3]结合基于关键路径的局部搜索和变邻域搜索方法，求解总拖期最小的大规模FJSP。ZHENG等[4]提出基于知识引导的果蝇优化算法，求解以最大完工时间最小为目标的双资源约束FJSP。而在生产实践中往往需要同时考虑多个目标，使得多目标FJSP成为了近年的研究热点问题。在这些研究中，初期多采用运筹学方法和启发式调度规则获取全局最优解。随着调度模型的复杂化和目标的多样化，遗传算法、免疫算法、蚁群算法、模因算法[5]、离散病毒算法[6]等智能算法开始广泛应用于多目标FJSP问题的求解。徐华等[7]提出一种混合离散蝙蝠算法，通过优先指派规则产生初始种群，同时采用位置变异策略实现快速搜索，有效地避免算法过早收敛。仲于江等[8]提出一种基于小生境粒子群算法，利用小生境技术计算得到粒子删除概率，并根据该概率值更新外部精英存档，从而保证算法能够获取更多优质的调度解。以上文献多为针对2个或3个目标的FJSP研究，4个目标及以上的高维多目标FJSP问题的研究较少。张超勇等[9]提出改进的非支配排序遗传算法能够有效求解以时间、成本、设备利用率等经济指标为优化目标的6目标FJSP问题，但得到的非支配解的数量过多，决策者很难直接从中筛选出最优的调度解。白俊杰等[10]在算法中引入偏好信息来引导粒子向决策者偏好的Pareto前沿收敛，一定程度上缩小了高维多目标FJSP的搜索空间。林震等[11]利用基于多交叉策略的元胞多目标遗传算法求解以瓶颈机器负荷、总机器负荷、加工成本、制造工期为目标的高维FJSP问题，通过改进的精英策略提升算法收敛速度。黄利福等[12]在粒子群算法中引入模糊理论，以模糊物元的相似度作为适应度值引导算法进化，求解优化多个经济指标的高维多目标FJSP。

随着社会节能环保意识的增强，柔性作业车间低碳调度也逐渐引起学者的重视。蒋增强等[13]提出基于设备状态能耗曲线的低碳策略，并设计基于血缘变异的非支配排序遗传算法解决算法过早收敛的问题。唐立力[14]提出改进的候鸟优化算法求解能耗目标最小的低碳调度问题。雷德明[15]提出一种基于新型优化机理的教学优化(TLBO)算法最小化总碳排放和平均延迟时间。张国辉等[16-17]对考虑机器速度的低碳FJSP模型展开研究，通过控制机器的加工速度以降低机器的碳排放总量。姜天华[18]提出改进的灰狼优化算法求解能耗成本和时间成本加权和最小的低碳调度模型。李明等[19]提出一种新型帝国竞争算法求解4目标的低碳FJSP问题，搜索到高质量的Pareto最优解。

总体而言，高维多目标FJSP和低碳FJSP是当前调度问题研究的热点和难点，但仍都处于起步阶段[20]。在高维多目标FJSP问题研究中，对于完工时间、拖期等经济指标的研究较多，而对于能量消耗等绿色指标的综合研究还较少。笔者综合考虑生产效率、机器利用率等经济指标以及能源消耗指标，建立了以最大完工时间、瓶颈机器负荷、总机器负荷、能量消耗为目标的高维多目标FJSP低碳调度模型。该模型不但更贴近生产实际，而且顺应了绿色制造的理念。在高维多目标FJSP中，随着目标维数的增多，种群中Pareto解的数量呈指数上升，传统的多目标优化方法选择压力不足，无法从众多Pareto解中筛选出最优调度解。为增强算法选择压力，获取一组均匀分布的优良调度解，笔者设计了改进的NSGA-Ⅲ算法求解高维多目标FJSP低碳调度问题。

1 高维多目标柔性作业车间低碳调度模型

1.1 高维多目标FJSP低碳调度问题描述

n个工件在m台机器上加工，每个工件都由若干道工序组成；每道工序可以在不同的机器上加工；工序加工时间和能量能耗与选择的加工机器相关。低碳调度的目标是为每道工序分配合适的机器，并确定每台机器上工序的加工顺序，以实现经济指标和绿色指标的协同优化。低碳FJSP模型还需满足以下约束条件：①某一时刻，同一台机器至多只能加工一个工件；②同一道工序只能在一台机器上加工；③工序在机器上加工时，不允许被中断，即加工是非抢占式的；④所有工件的优先级相同；⑤不同工件的工序之间不存在先后约束，同一工件的工序间存在顺序约束关系；⑥所有零件在t=0时刻都可以被加工。

1.2 高维多目标FJSP低碳调度模型

1.2.1 参数与变量设置

为更好地描述高维多目标FJSP低碳调度模型，定义以下参数和变量：n为工件总数；m为机器总数；J={J1,J2,…,Jn}为工件集合,i=1,2,…,n；M={M1,M2,…,Mm}为机器集合,k=1,2,…,m；hi为工Ji的总工序数;Oij为工件i的第j道工序,其可选加工机器数为mij；tijk、qijk、eijk分别表示工序Oij在机器Mk上的加工时间、加工功率和加工能耗；sij、cij分别为工序Oij的开始加工时间和完工时间；Ci为工件Ji的完工时间；当工序Oij在机器Mk上加工时，xijk=1，否则xijk=0；工序Oij先于工序Ohl在Mk上加工时，ykijhl=1，否则ykijhl=0；L为一个很大的正整数。

1.2.2 能量消耗指标

生产过程中资源消耗包括机器加工产生的能量消耗以及工件原材料、切削液等物料资源消耗，其中受调度方案影响的是加工电能消耗[21]。因此，笔者采用电能消耗作为能量消耗指标的度量，能量消耗系数矩阵可表示为：

E={eijk}m×n

(1)

机械加工过程中，机器维持自身运转需要消耗很大一部分功率，即机器空载功率qu。当机器空闲时，输入功率全部用于机器空转。当机器加工工件时，输出功率ql的一部分用于维持机器自身运转，另一部分用于承担负荷带来的功率损耗，即载荷损耗功率qa，其余用于完成工件的切削加工，即切削功率qc。则机器的功率平衡方程[22]可表示为：

ql=qu+qa+qc

(2)

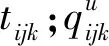
(3)

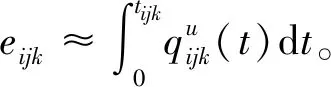
(4)

因此，可利用机器空载功率和工序加工时间数据建立能量消耗系数矩阵，计算机器加工的能量消耗，然后通过比较不同调度方案下能量消耗总量的大小筛选出节能的调度方案。

1.2.3 调度模型建立

笔者综合考虑生产效率、设备利用率和能量消耗等指标，建立了考虑能量消耗的多目标低碳FJSP调度模型。模型包含4个优化目标：最大完工时间最小(CM)、瓶颈机器负荷最小(WM)、机器总负荷最小(WT)、机器能量消耗最小(ET)。

目标函数：

(5)

(6)

(7)

(8)

约束条件：

sij+xijk×tijk≤cijk

(9)

cij≤si(j+1)

(10)

sij+pijk≤shl+L(1-ykijhl)

(11)

cij≤si(j+1)+L(1-ykihl(j+1))

(12)

(13)

式(9)和式(10)表示同一个工件的工序存在先后顺序，工件的前一道工序完成后才能加工下一道工序；式(11)和式(12)表示在同一时刻，同一台机器只能加工一道工序；式(13)表示机器资源约束，即同一道工序在同一时刻只能在一台机器上加工。

2 改进的NSGA-Ⅲ算法

为求解高维多目标FJSP低碳调度问题，设计了改进的NSGA-Ⅲ调度算法。首先，利用快速非支配排序算法对种群进行排序；其次，在高维目标空间中引入均匀参考点，利用基于参考点的小生境选择机制筛选出优良个体。基于参考点的小生境选择把目标空间划分为多个子区域，算法可以在多个子空间中均匀搜索，在保证算法收敛性的同时提高了解的多样性[25]。改进的NSGA-Ⅲ算法的具体流程如下：

(1)初始化参考点和遗传算法参数，设计染色体编码，利用随机初始化方法生成初始化种群P0，种群个体数为N。

(2)执行交叉变异产生第v代子代种群Qv，合并第v代子代种群与父代种群Pv，得到个体数为2N的种群Rv=Pv+Qv。

(3)利用基于Pareto支配的快速非支配排序法对种群Rv进行排序，获得各个支配层个体F1、F2、…、Fw，l=1，2,…,w。

(4)从第一层非支配层开始，依次将非支配层中的个体加入到新种群Sv中，直到Sv中的个体大于等于N，其中使得Sv中个体数首次大于等于N的最后一层非支配层为Fl。

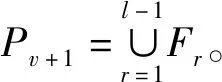
(6)利用基于参考点的小生境选择机制从最后一个非支配层Fl中选择出K=N-|Pv+1|个个体，得到新种群Sv。

(7)迭代直至满足最大迭代次数。

2.1 编码与解码

采用基于工序和基于机器相结合的双层编码方法，分别确定工序排序和机器分配。基于工序部分的编码长度等于所有工件的总工序数，每个工件的工序用相应的工件号表示，工件号出现的顺序即为工序的加工顺序。基于机器的编码长度也等于所有工件的总工序数，染色体从左到右依次按照工件号和工序的顺序进行排列。基因位上的整数表示当前工序选择的机器在可选机器集中的顺序编号，保证了后续遗传操作产生的解仍是可行解。

基于该编码方式，采用插入式贪婪解码算法进行染色体解码，确保产生活动调度解。依次读取染色体的工序，将工序插入到可利用的机器空闲间隔时间中以减少机器空转，从而提高机器利用率、缩短最大完工时间。

2.2 交叉与变异

笔者针对双层编码选用不同的交叉操作，基于工序的编码采用改进的基于工序优先顺序(IPOX)的交叉方法，基于机器的编码采用多点交叉(MPX)操作。IPOX交叉方法仅交叉父代染色体中工序的加工顺序，不改变机器分配。首先将工件随机分成两个子集J、J′；然后将父代中包含J的工件复制到子代C1，P2中包含J′的工件复制到子代C2，保持位置和顺序不变；将P2中包含J′的工件按顺序插入C1空白处，P1中包含J的工件插入C2。MPX交叉操作仅交叉父代染色体中工序的加工机器，不改变加工顺序。随机生成一个与机器染色体等长的0、1数列R；选出P1、P2中与R中的“1”位置对应的机器号，交叉复制到C2、C1，保持原有的位置和顺序；将P1、P2中剩余的基因复制到C1、C2。

变异操作通过对染色体施加小规模扰动以增加种群多样性，笔者对双层编码采用不同的变异方式。基于工序的编码执行插入式变异，在工序排序部分随机选择一个基因，插入到另一个随机的基因位并保持工序的机器分配不变。基于机器的编码在执行变异时，随机选择染色体上的r个基因，依次在各工序的加工机器集中随机选取机器进行替换。

2.3 基于参考点的小生境选择机制

2.3.1 归一化目标值和参考点

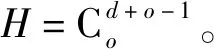
(14)

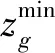
(15)

2.3.2 关联参考点

连接参考点与标准化超平面的原点构造基于参考点的参考线，计算种群中的每个个体到参考线的垂直距离。选择与参考线垂直距离最短的个体，将该个体与对应的参考点关联。三维目标空间中关联参考点的示意图如图1所示，其中空心点表示目标空间中的均匀参考点，虚线表示基于参考点的参考线，与虚线连接的实心点表示与该参考点相关联的种群个体。

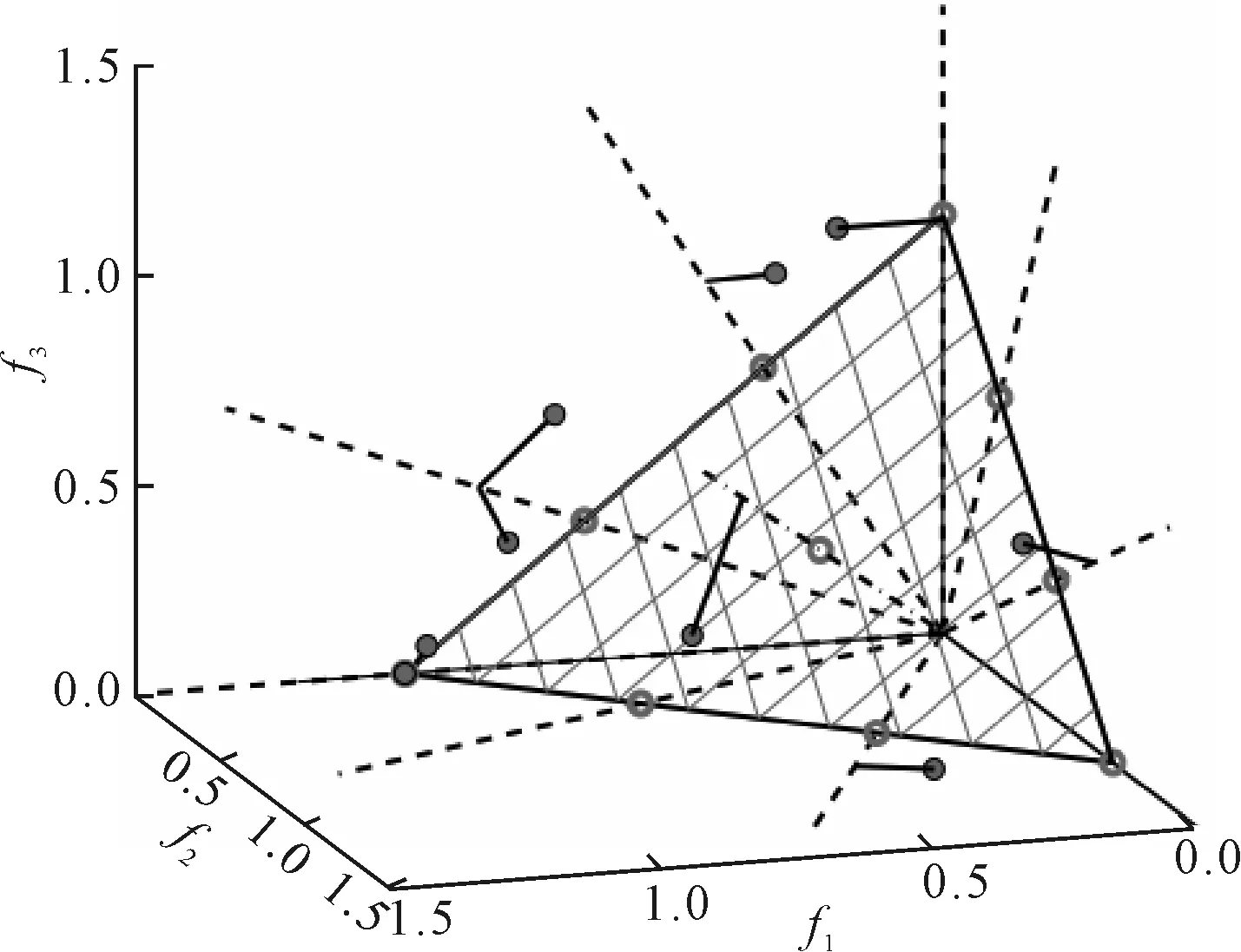
图1 三维目标空间关联参考点示意图

2.3.3 小生境选择机制

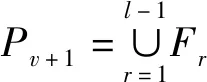
3 实例验证分析

3.1 实验平台及参数设定

改进的NSGA-Ⅲ算法采用Matlab 2016a编程，程序在CPU主频2.20 GHz，内存4G的计算机上运行。选取Kacem基准问题中的3种不同规模的基准实例进行测试，包括8×8 P-FJSP、10×10 T-FJSP、15×10 T-FJSP。由于基准实例中没有功率数据，笔者采用随机函数生成法生成功率数据，功率数据为1～5之间的随机整数。合理的参数设置很大程度影响算法的性能，为保证算法的求解质量和运行效率，参考文献[27]和文献[28]中的参数，设置实验参数如下：交叉概率为0.7，变异概率为0.1，种群个体数为120，最大迭代次数T为200，参考点个数H为120。

3.2 仿真结果分析

选取3种不同规模的基准实例，验证改进的NSGA-Ⅲ调度算法求解不同调度问题的有效性。其中10×10 T-FJSP、15×10 T-FJSP基准实例是完全FJSP调度问题，允许每个工序在所有可选机器上加工，8×8 P-FJSP是部分FJSP问题。8×8 P-FJSP规模实例的一组解甘特图如图2所示，相应的目标值分别为CM=15，WM=12，WT=74，ET=222；10×10 T-FJSP规模实例的一组解甘特图如图3所示，相应的目标值分别为CM=8，WM=7，WT=44，ET=128；15×10 T-FJSP规模实例的一组解甘特图如图4所示，相应的目标值分别为CM=15，WM=15，WT=104，ET=26。

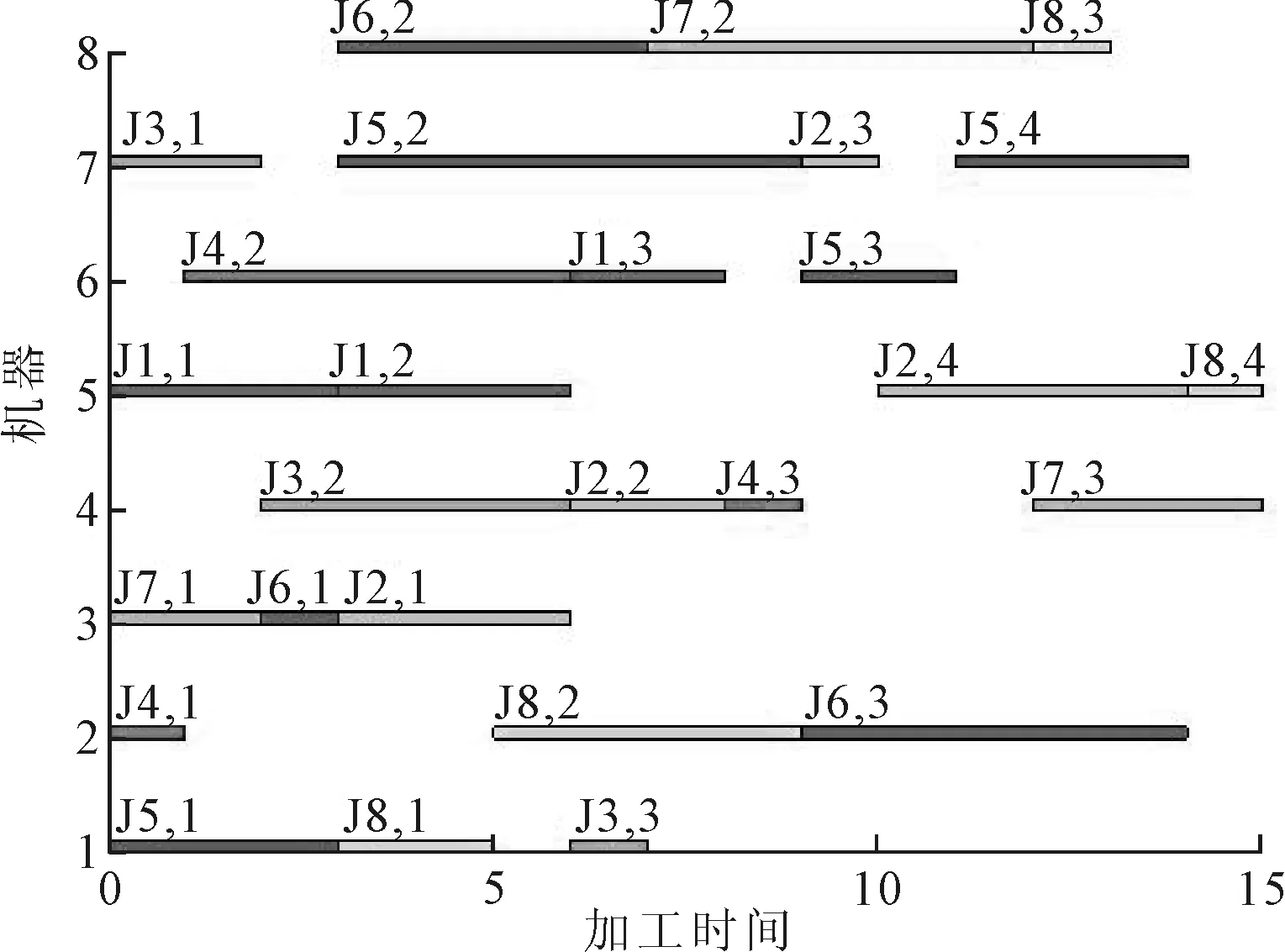
图2 8×8 P-FJSP甘特图

图3 10×10 T-FJSP甘特图

图4 15×10 T-FJSP甘特图

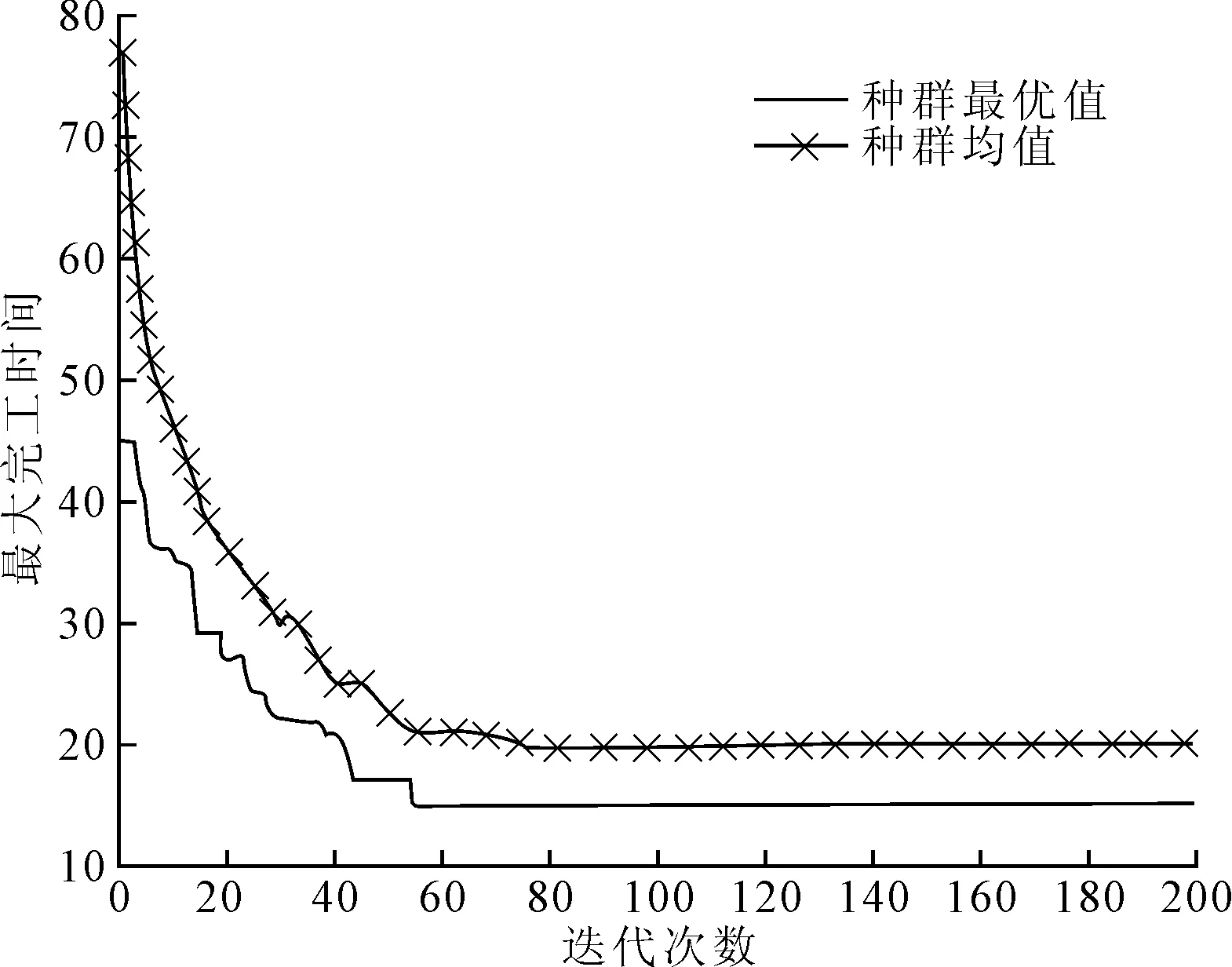
图5 改进的NSGA-Ⅲ算法的最大完工时间收敛曲线

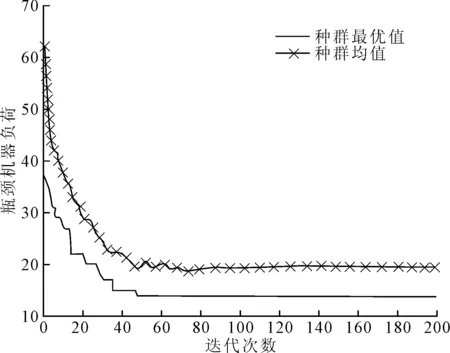
图6 改进的NSGA-Ⅲ算法的瓶颈机器负荷收敛曲线

改进的NSGA-Ⅲ调度算法求解15×10 T-FJSP问题的最大完工时间收敛曲线如图5所示，瓶颈机器负荷收敛曲线如图6所示，总机器负荷收敛曲线如图7所示，能量消耗收敛曲线如图8所示。可以看出，4个目标在60代时均收敛于最优值，说明在60代已达到4个目标的综合优化。该结果表明NSGA-Ⅲ调度算法具有较强的选择压力，能够在高维目标空间中均匀搜索，快速收敛得到均衡各目标的低碳调度解。

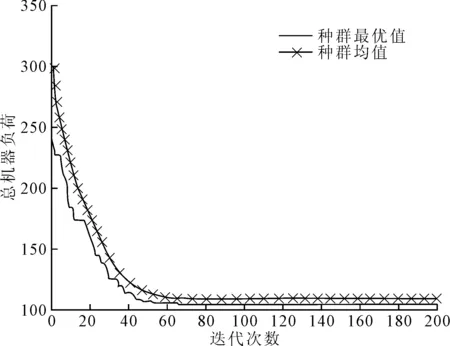
图7 改进的NSGA-Ⅲ算法的总机器负荷收敛曲线

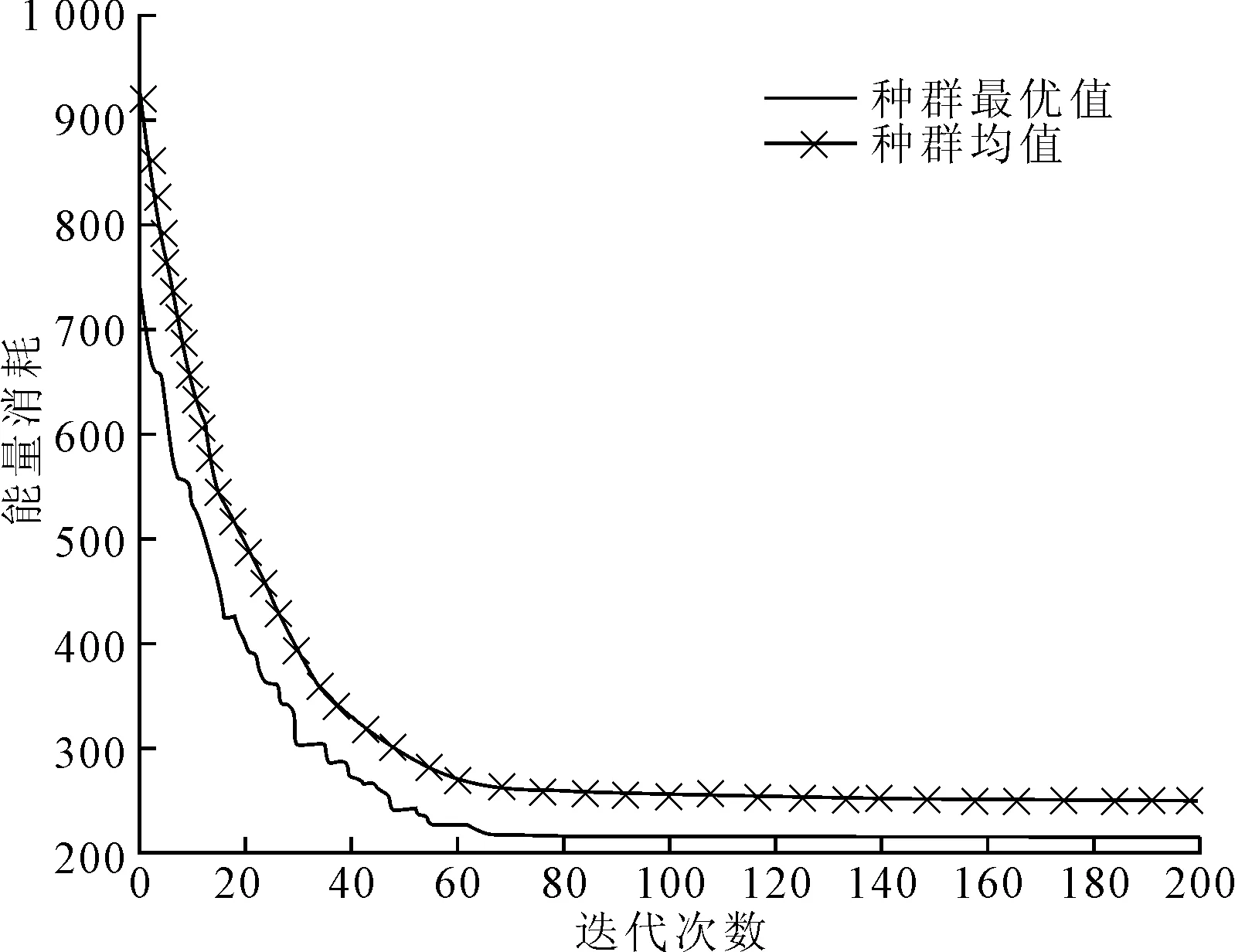
图8 改进的NSGA-Ⅲ算法的能量消耗收敛曲线

3.3 算法结果对比

为验证算法中基于参考点的小生境选择机制的有效性，选取与NSGA-Ⅲ算法框架相似的NSGA-Ⅱ算法对3种不同规模的基准实例的运行结果进行对比。采用文献[29]中的解质量指标(QS)和空间分布度(DS)指标作为解的分布性度量指标。QS表示算法的解在新的Pareto解集合中所占的比例，用于衡量解集的非支配性。即把两种算法的解集进行对比，生成新的非支配解集合，并计算其中属于各自算法的解的比例。QS越接近1，表明该算法的求解质量越高。DS表示非支配解在Pareto前沿上分布的均匀程度，通过解集中个体之间的距离测度。DS越小，则该非劣解集的分布越均匀。T表示算法收敛到最优值的时间，由算法多次运行后取平均值得到。T越小，则算法收敛速度越快。对比实验结果如表1所示。

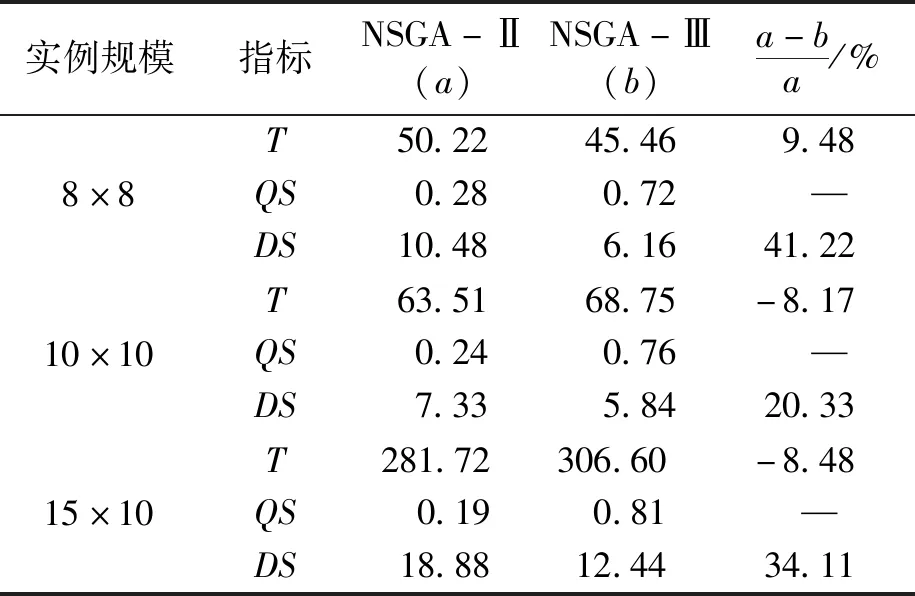
表1 Kacem测试集实验结果对比表

由表1可知，改进的NSGA-Ⅲ算法的解质量指标(QS)、空间分布度指标(DS)均优于NSGA-Ⅱ算法，且随着基准实例规模的增大，NSGA-Ⅲ算法的QS值越优。这表明改进的NSGA-Ⅲ调度算法能够有效求解较大规模的FJSP问题，获得均匀分布的优良调度解。该结果体现了基于参考点的小生境选择机制的有效性，能够在高维目标空间中均匀搜索，获得优良的Pareto非支配解。

从收敛时间T看，在8×8 P-FJSP中，改进的NSGA-Ⅲ算法的收敛速度稍快于NSGA-Ⅱ算法，而在另外两个规模稍大的实例中，改进的NSGA-Ⅲ算法的收敛速度稍差于NSGA-Ⅱ算法，二者相差比例均在10%以内。其原因是两种算法都是利用快速非支配排序法对种群进行排序，而随着目标空间的扩大，基于参考点的小生境选择机制的计算复杂度略大于NSGA-Ⅱ算法的拥挤距离计算。总体而言，两种算法在收敛速度方面表现基本相当。

综上所述，改进的NSGA-Ⅲ算法具有与NSGA-Ⅱ算法基本相同的收敛速度，得到的非支配解的质量明显优于NSGA-Ⅱ算法。因此，改进的NSGA-Ⅲ算法能够有效求解高维多目标低碳FJSP问题，获得一组均匀分布的低碳调度解。

4 结论

笔者采用改进的NSGA-Ⅲ调度算法求解综合考虑最大完工时间、瓶颈机器负荷、总机器负荷和能量消耗指标的高维多目标FJSP低碳调度模型。在分析机器能量消耗指标的基础上建立机器能量消耗矩阵，提出了综合考虑经济指标和能量消耗指标的高维多目标FJSP低碳调度模型。为解决传统多目标优化方法在高维多目标FJSP问题中选择压力不足的问题，设计了改进的NSGA-Ⅲ调度算法。实验结果表明基于参考点的小生境选择机制能够在高维目标空间中高效搜索，在增强算法选择压力的同时提升种群多样性，获得一组较优的低碳调度解。但算法的收敛速度还有待提高，未来将考虑通过改进支配关系进一步提高算法的搜索效率和收敛速度。另外，笔者考虑的是静态环境下的低碳FJSP，忽略了实际生产过程中的动态因素。在实际生产过程中，往往存在机器故障、工件延迟、紧急订单插入等不确定因素。因此，进一步研究动态环境下的低碳调度也是一个重要的研究方向。