震后救灾网络中应急资源配置鲁棒优化研究

郝西浩，张 玲

(福州大学 经济与管理学院，福建 福州 350116)

近年来，大规模地震灾害频繁发生，造成了严重的人员伤亡和财产损失。如2008年的汶川大地震，2010年的青海玉树地震，2013年的四川雅安地震，2017年的九寨沟地震。地震灾害的发生具有不确定性、动态性、复杂性等特征，使得灾害发生后应急救援过程应急资源需求具有不确定性、持续时间长、需求量大等特点，决策者往往在短时间内难以全面、准确地掌握灾情信息，要求决策者能基于这些不确定性信息对应急资源保障网络的规划和资源优化配置作出相应的决策。

在灾害保障网络规划和资源优化配置研究方面,HAGHI等[1]考虑到需求和物资成本的不确定性，建立了一个以对伤员医疗需求的响应时间最大、响应阶段的总成本最小为目标的多目标规划模型，为了处理不确定性，使用了鲁棒优化方法，并用ε-约束方法求解模型。HU等[2]提出了一个考虑提前期折扣、退货价格和权益的两阶段随机规划模型，将灾难前库存水平和灾难后采购数量的决策与供应商选择整合在一起，采用基于场景的方法来表示需求的不确定。ALEM等[3]考虑预算分配、多周期、多类型车辆、购买物资及交货时间等因素，建立了两阶段随机网络流模型，并且提出一种启发式算法求解该模型。盛虎宜等[4]基于公平视角研究震后初期灾区应急物资短缺情景下的定位-路径问题 ，以总配送时间最短作为应急物资配送的效率性衡量指标，在此基础上构建双目标LRP模型，并基于分层序列法思想设计一种二阶段混合启发式求解算法。李双琳等[5]针对震后初期应急物资配送系统优化问题，考虑应急物资需求模糊情况下应急物资配送中心选址和应急物资多式联运安排的集成决策，以应急物资配送总时间最短和受灾点应急物资未满足的总损失最小为目标，建立了一个震后应急物资配送的多目标选址-多式联运问题优化模型。王绍仁等[6]针对震后紧急响应阶段的应急物流系统优化问题,建立了一个两级设施定位-运输路线安排问题模型(LRP)。彭春等[7]考虑资源成本的不确定性，提出了多类应急资源配置的鲁棒选址-路径优化。张乃平等[8]考虑地震后道路存在严重损毁的情况,为提高此时应急物资配送的公平性和时效性,构建以应急物资分配公平性最大和运输总时间最小为目标的多物资、多出救点和多受灾点的分配-运输模型。ZHANG等[9]考虑主要灾害和次生灾害情景下的应急资源分配问题，提出了一个基于条件概率的情景树来定义主要灾害和次生灾害之间相关性的三阶段多目标随机规划模型，可以最大程度地减少运输时间、运输成本和不满意的需求，为了计算可处理性，提出了一种近似的单阶段随机规划方法。BARON等[10]分别基于盒形不确定性集合和椭球不确定性集合,建立了一个多周期选址-生产-分配优化模型，分析推导出了原模型的鲁棒对应模型。SADJADI等[11]针对灾后救援初始阶段所面临的不确定性需求和运输成本，建立了一个基于鲁棒优化的单目标选址分配优化模型,给出了模型的鲁棒对应形式。朱佳翔等[12]针对应急物流配送过程中救灾信息的多重不确定性特点,兼顾考虑“灰”与“鲁棒”等双重交叉不确定性因素的影响,构建了应急物流配送多阶段多目标灰动态规划模型,并在此基础上给出鲁棒控制策略。张志霞等[13]考虑应急响应系统中多种应急物资需求的不确定性,建立最小化总成本和总时间的多目标-两阶段临时配送中心选址和应急资源调度模型，采用相对鲁棒优化方法求解模型,利用区间估计描述不确定性因素,并引入扰动系数和控制参数调节模型的鲁棒性和最优性。俞武扬[14]提出了灾害发生前的应急物资配置问题具有两个重要的不确定性, 即交通网络中受自然灾害影响而阻断的道路和受灾点的应急物资需求量，建立了不确定网络结构下的两阶段应急物资鲁棒配置模型。DONYA等[15]考虑在灾后启用备用供应商提供物资，并增加分配中心的使用，建立了一个可靠的鲁棒优化模型，提出了基于拉格朗日松弛法的模型求解方法。

综上所述，国内外目前对于灾前应急设施选址、资源配置的研究较多，但关于基于鲁棒优化的应急设施选址和资源配置等方面的研究成果还较少，对于灾后资源需求点、资源供应点共同约束下确定应急物流中心选址与资源配置的研究也较少。而且，大多数的震后定位-路径问题研究只考虑了大规模灾害发生后的单级配送，不经过中转站即直接从供应点向需求点运输物资，这样的研究缺乏一定的现实意义。因此，笔者考虑灾区需求的不确定性及资源配置中救援物资与运输工具之间的协调性，着力解决灾后的应急资源配置问题。运用鲁棒优化的方法，建立了一个多目标应急资源鲁棒配置优化模型,推导出了所建模型的鲁棒对应形式,提出了求解多目标优化模型的方法。

1 问题描述

震后应急物资保障网络主要由应急物资供应点、临时救灾中心和需求点3方面构成。在救援过程中，选择离灾区最近的国家应急物资储备仓库作为应急物资供应点，在受灾点附近建立若干个临时救灾中心承担救援物资的中转、存储及再分配等功能。灾区需求点所需的大批量、多批次、多品种的物资需要从临时救灾中心通过卡车和直升飞机向灾区进行运输，以使需求点的综合不满足量最小。假设有若干候选应急物资供应点、临时救灾中心、受灾需求点和不同类型的应急物资运输设备。其中公路运输为卡车运输，空中运输为直升机，在运输设备允许工作时间内可以反复派出执行配送任务。震后应急资源保障网络示意图如图1所示，其中双向实线箭头表示临时救灾中心通往需求点的道路没有受损，运输交通工具(卡车和直升机)可以在运送完物资后返回到临时救灾中心，双向虚线箭头表示道路受损，此时只能通过直升机进行物资运送。笔者主要考虑受灾点需求的不确定性及各类应急物资的分配量与运输工具之间的协调性，以实现需求点的不满足总量最小和整个系统的救援响应时间最小。

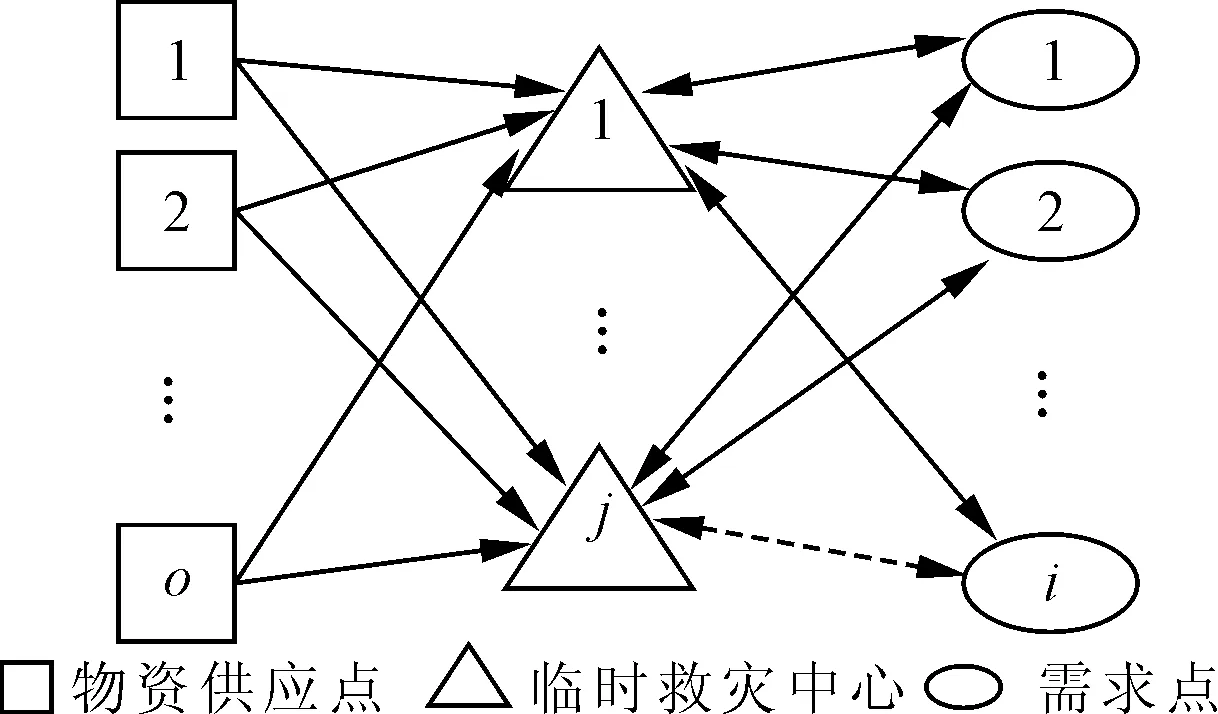
图1 震后应急资源保障网络示意图

2 震后初期应急资源配置鲁棒优化模型

2.1 符号说明

(1)相关参数定义。I表示应急物资需求点的集合；J表示临时救灾中心集合；O表示应急物资供应点的集合；M表示应急资源种类集合；Wom表示供应点o储备的应急资源种类m的数量；L表示临时救灾中心和需求点之间进行物资运送的工具集合；qlm表示运输工具l每次可以运输物资m的有效数量 ；dim表示需求点i对第m种物资的需求量；Vl表示可以到临时救灾中心的运输工具最大数量；Tl表示运输工具l的可工作时间的最大值；fjil表示单位时间内从临时救灾中心j到需求点i的运输工具l的流量限制；fijl表示单位时间内从需求点i到临时救灾中心j的运输工具l的流量限制；ξm表示应急物资m不满足量的权重；tjil表示运输工具l从临时救灾中心j到需求点i单次运输所花费的时间；Φ表示一个非常大的实数。

(2)决策变量。xojm表示物资供应点o向临时救灾中心j供应的物资m的数量；yjim表示临时救灾中心j向需求点i供应的物资m的数量；zjl表示运输物资到临时救灾中心j的运输工具l的数量；Njilm表示运输工具l从临时救灾中心j向需求点i运输物资m的次数；Nijl表示运输工具l从需求点i回到临时救灾中心j的次数；Tijl表示临时救灾中心j的运输工具l向需求点i运送完救灾物资所耗费的时间；rim表示需求点i未满足的物资m的数量。

2.2 需求确定下的应急资源多目标优化配置模型

根据上述相关参数设置，建立需求确定下的应急资源配置多目标优化模型。

(1)

(2)

(3)

(4)

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

Nijl≤fijlTijl≤Φ·Nijl，∀i,j,l

(13)

(14)

i∈I,j∈J,l∈L,o∈O,xojm、yjim、Tijl∈R+,

zjl、Njilm、Nijl∈Z+

(15)

需求确定下的应急资源配置模型包含两个优化目标：目标函数式(1)表示最小化系统的所有不满足量；目标函数式(2)表示最小化任意的临时救灾中心和需求点之间的任意一类交通运输工具的最大工作时间，即等价于整个系统的救援响应时间最小。约束式(3)表示物资供应点o向临时救灾中心运送的物资m不能超过该供应点的储备数量；约束式(4)表示临时救灾中心向需求点运送的物资m的数量不超过临时救灾中心从供应点获取的物资m的数量；约束式(5)表示从临时救灾中心运送到需求点的物资数量不超过需求点的需求量；约束式(6)表示各临时救灾中心j可用的交通工具的总和不能超过此类交通运载工具的最大可用数量；约束式(7)表示临时救灾中心j的运输工具l运输完物资后从需求点返回临时救灾中心所耗费的时间不超过此类运输工具总的最大工作时间；约束式(8)表示从临时救灾中心向需求点i运输物资m的总量和这两个节点之间往返运输次数的关系；约束式(9)主要是为了避免模型的结果中出现yjim=0而Njilm≠0的情况；约束式(10)和式(11)表示临时救灾中心和需求点之间的任何一种交通工具的流量守恒；约束式(12)和式(13)表示临时救灾中心和需求点之间往返的运输量与其运输所耗费的总时间之间的关系；约束式(14)表示需求点不满足量的计算关系；约束式(15)表示模型中变量的约束。

2.3 需求不确定下的应急资源鲁棒优化配置模型

由于灾害的突发性，受灾点对救援物资的需求往往不确定，而这种不确定性会导致模型的求解困难。针对需求的不确定性，采用BERTSIMAS等[16]提出的鲁棒优化方法求解模型,以解决需求参数不确定性对模型求解的影响,达到模型解的鲁棒性和模型目标的最优性之间的折衷平衡。

上述多目标优化模型中只有约束式(5)和式(14)中包含需求不确定性参数dim，接下来介绍相关约束的鲁棒对应式的推导过程。式(5)中只有一个不确定性参数dim，为了建立对应的鲁棒优化模型，必须要使约束条件中出现更多的不确定性需求参数。所以，对约束式(5)做如下的等价转换：

(16)

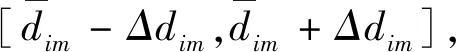
其中,δim通过求解线性规划式(18)得到：

(18)

式(18)的对偶形式为：

(19)

将式(19)代入式(17)，可以得到：

(20)

通过分解式(16)，可以避免松弛解的产生。其中变量gim的对偶变量为δim，为了分解式(20)，将变量gim的下标i集合扩展到全集I。通过这种变换，变量gim可以转换成为：

(21)

将式(21)代入式(20)，并且将其按照需求点进行分解，可以得到：

(22)

对于约束式(14)的鲁棒对应式转换与约束式(5)的变换思路类似，先将约束式(14)做如下的等价转换：

(23)

其中，λim通过求解线性规划式(24)得到：

(24)

式(24)的对偶形式为：

(25)

将式(25)代入式(23)，并按照需求点进行整理可以得到：

(26)

3 鲁棒优化模型的求解方法

通过以上约束的鲁棒对应式的转换，可以得到原模型的鲁棒对应模型，原模型中的式(5)和式(14)分别被式(22)和式(26)所替换，得到的鲁棒对应模型是一个多目标整数规划模型，将多目标优化模型转换成单目标优化模型更有利于模型的求解。

由于目标函数式(1)表示最小化系统的所有不满足量；目标函数式(2)表示最小化任意的临时救灾中心和需求点之间的任意一类交通运输工具的最大工作时间，即等价于整个系统的救援响应时间最小。在震后的应急资源配置过程中，对灾害的响应时间往往比满足灾区的全部需求要更加重要，因此用主次兼顾法将多目标鲁棒优化模型转换为单目标模型。

β=minobj1

(27)

约束条件包括式(3)、式(4)、式(22)、式(6)～式(13)、式(26)、式(15)。

该方法就是先不考虑救援的响应时间，只是求解单目标鲁棒优化模型式(27)，由此可以得到最小化系统的所有不满足量β，再求解以下的单目标优化模型。

minT

(28)

先求解式(27)得到β，再将其代入式(28)中求解，就可以得到整个系统的应急响应时间和相应决策变量的取值。

4 算例分析

笔者采用CPLEX软件进行具体的模型求解，算例选用2010年4月14日在青海玉树县发生的7.1级地震作为研究对象，选择受灾中心区域的8个地区作为受灾需求点，考虑到临时救灾中心建设成本的因素，不应设置过多，而且要便于车辆运输物资，因此选取受灾较轻的3个地区作为临时救灾中心，具体如图2所示。

笔者仅考虑两种灾后救灾点需要的物资(帐篷和食物)，各个需求点的需求量如表1所示。因为存在震后道路损毁的可能，不利于大型运输车辆进行运输，所以假设只有两种型号货车作为陆上运载工具，载重能力分别为1.5 t的小型货车和2.5 t的中型货车，空中运输工具为载重量1.5 t的直升机。假定两种型号货车的最大工作时间均为28 h，直升机的最大工作时间为8 h。临时救灾中心到需求点的陆上交通工具的通行流量如表2所示。

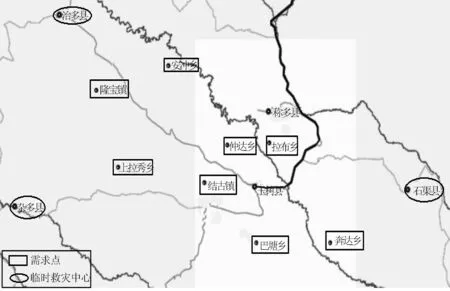
图2 临时救灾中心和需求点的位置分布图

表1 各个需求点的应急物资需求量

表2 临时救灾中心到需求点的陆上交通流量限制 辆次/h

货车和直升机从临时救灾中心j到需求点i单次运输所耗费时间Tijl分别如表3和表4所示。此外，假设从石渠县到隆宝镇的陆上通行道路被毁，无法通行，将其运输时间设置为一个很大的实数。

表3 货车从临时救灾中心到物资需求点单次运输耗费时间 h

表4 直升机从临时救灾中心到物资需求点单次运输耗费时间 h

假设地震灾区附近有4个国家应急物资储备中心(救灾物资供应点)，各个物资供应点的储备容量如表5所示，每一类应急救灾物资的权重都取0.5。

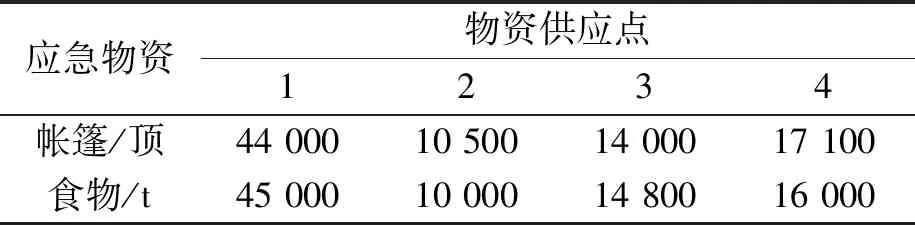
表5 各个物资供应点储备的物资数量

经过编程计算可以得到货车数量变化情况下需求点的总不满足量和未使用量结果，如表6所示，其中，使用直升机的数量设置为48架。由表6可知，当使用的货车数量在600～970辆之间时，随着小货车数量的增加，所有救援需求点的全部不满足量之和及未被利用的应急物资都在逐渐减少，说明影响灾后救援的主要问题在于临时救灾中心和需求点之间可以利用的物资运输工具。由此可见，笔者建立的模型能够分析出在地震灾害发生后整个应急救灾系统存在的主要问题，尤其是需求点所需要的救援物资和运输物资的交通工具之间的紧密关系。

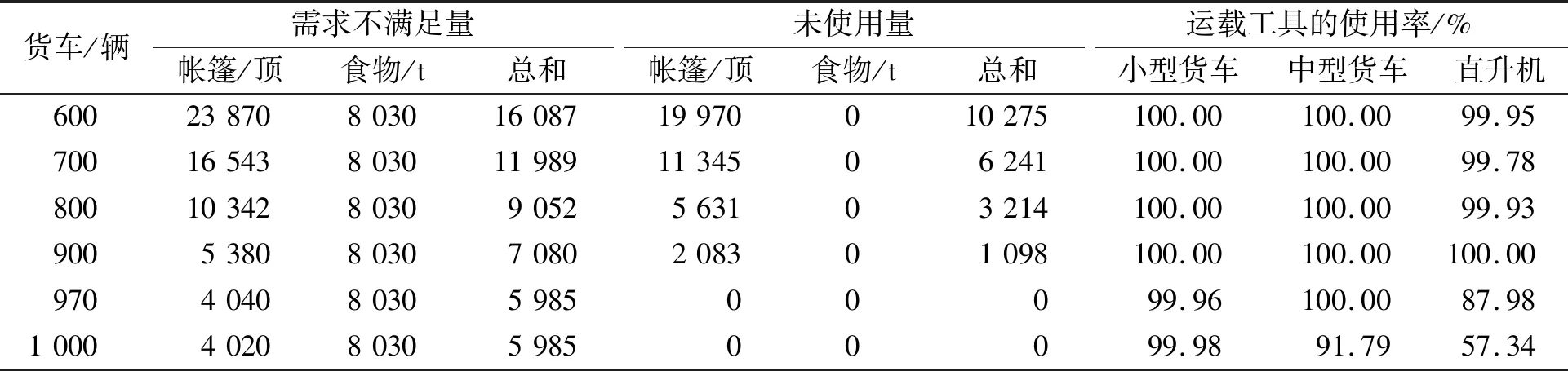
表6 货车数量变化情况下需求点的总不满足量和未使用量

需求不确定情况下，需求的变化会导致整个模型目标值的变化，因此要确定一个需求变化的区间范围。笔者基于需求在其名义值左右5%、10%、15%的变化范围内组成3个需求变化区间。随着需求变化的同时，改变Γ的取值，求解得到需求不确定情况下优化模型的目标值，如表7所示。

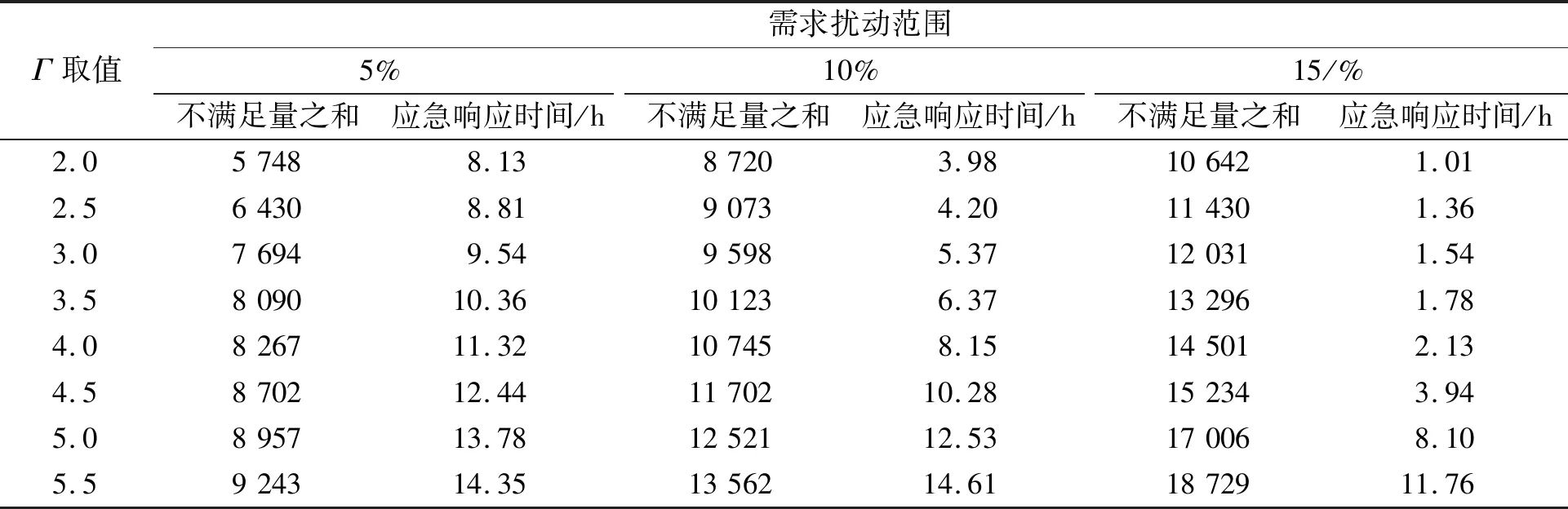
表7 需求不确定情况下优化模型的目标值

从表7可以观察到：在Γ保持不变的情况下，需求在其名义值左右扰动范围越大，整个救灾系统的不满足需求量之和也会越来越大，但是整个应急救援的响应时间在下降，这是因为救援响应时间的计算是在系统不满足量之和的基础上进行的；在需求扰动区间范围保持不变时，随着Γ取值越来越大，整个系统的不满足量之和与应急救援响应时间均随之增长，体现了Γ在平衡决策模型的最优性和鲁棒性之间的效果。

5 结论

笔者通过建立相应的应急资源优化配置模型，解决了地震灾害发生后整个应急救灾网络中应急资源优化配置的问题，同时考虑了临时救灾中心和需求点之间交通运输工具的分配问题。在求解模型时，针对地震灾害造成的应急需求在一定的区间变化的特点，利用鲁棒优化处理不确定性，实验结果验证了该模型在需求不确定性情况下能够体现模型目标函数的鲁棒性和最优性之间的均衡，能够为应急救灾部门在灾后的应急救灾工作中提供参考和决策支持。然而笔者仅仅考虑了灾后需求的不确定性，而在应急资源配置过程中，还可以考虑资源成本、路径中断等不确定性。同时考虑多目标、动态多阶段的应急资源配置问题，将是未来研究的一个方向。