二维非线性阻尼Navier-Stokes方程弱解的存在性

熊坤翠，姜金平，张亦驰，刘文婧

(延安大学 数学与计算机科学学院，陕西 延安 716000)

我们讨论如下的二维Navier-Stokes方程：

(1.1)

其中，u=u(x,t)∈2表示速度，p表示压力项，f(x)表示外力项；Ω表示在2上的光滑区域，∂Ω是表示Ω的边界，v>0表示流体的运动粘性系数；在阻尼项中，c>0,β≥0二者都是常数。

对于Navier-Stokes解的存在性的探讨在文献[1-3]等都有一定的研究。本文通过Galerkin方法讨论了当二维Navier-Stokes方程增加非线性阻尼时，它的弱解存在。

1预备知识

给出Sobolev空间的定义：对p≥1,m是非负整数，则：Wm,p=LP(Ω)∩{u|Dαu∈Lp(Ω),|α|≤m}={u|u∈LP(Ω),Dαu=LP(Ω),|α|≤m}，通常用LP(Ω)与Hr(Ω)表示Sobolev空间，在他们上面的内积分别为u=(u1,u2)和v=(v1,v2)在空间H1(Ω)的范数记为

‖u‖=‖u‖H1=‖▽u‖L2=

LP(Ω)空间中的范数为：

|u|p=‖u‖p=ʃΩ|u|pdx。

如下Poincare’不等式成立：

λ1|u|2≤‖u‖2。

(2.1)

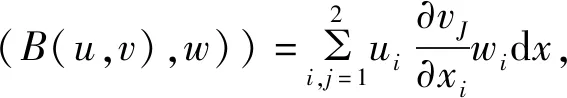
B(u,u,v)=0,B(u,v,w)=-(B(u,w),v)，

由文献[4]可知，对每一个u,v∈D(A)，有

及|B(u,v,w)|≤

给方程(1.1)两边同时作用投影算子P得：

2 弱解的存在性

定义1[2]设f∈L2(Ω)，对任意T≥0，若函数对(u(x,t),p(x,t))满足以下性质：

(1)u∈L2(0,t;V)∩L∞(0,t;H)∩

Lβ(0,T;L2(Ω))，

定理1 设f∈L2(Ω)，u0∈V及P≥0，则对于任意给定的T≥0，方程(1.1)存在弱解u，使得u∈L2(0,T;V)∩L∞(0,∞;H)∩Lβ(0,T;L2(Ω))。

我们先定义方程(1.1)的弱解。

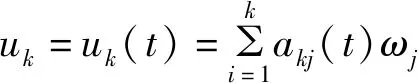
c(|u|β，ωj)uk=(f,ωj)，

j=1，2，…k,uk(0)=u0k，

(3.1)

将方程(1.1)与uk做内积得：

穆尔通过动物寓言故事反映人类生活，尽管它们是寓言性的，反映的是现实生活。穆尔在动物世界里找到了自己的生活，展示了一个丰富的自我。从文化批评的角度看，她笔下的动物大多为雌性动物或与女性有关，体现了诗人对女性的关怀。穆尔以严肃的创作态度描写动物、了解动物、尊重动物。她笔下的人与动物是互补的关系。穆尔通过动物诗歌提醒我们，自然界的生灵时刻受到人类的侵扰和控制，人类总是试图成为大自然的主宰。穆尔明确提出，动物有着它们自己的权利，值得被尊重；人类应该学习和模仿自然，而不是控制和征服自然。

c‖uk‖β+2=(f,uk)，

(3.2)

再利用Young’s不等式和Hölder不等式，得：

再整理得：

(3.3)

再利用(2.1)得：

由Gronwall’引理，可得：

|uk|2≤

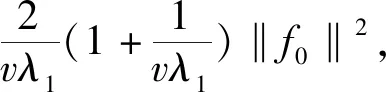
(3.4)

在(3.3)式两边对时间t积分得：

∀m>0，

(3.5)

根据(3.4)和(3.5)得到：

(3.6)

因此uk在L∞(0，T；H)，L∞(0,T;V)，Lβ(0,T;L2(Ω))中有界，又因为B(u,v,w)=0和

可知：‖B(φ),φ‖≤c|φ|1‖φ‖2，∀φ∈V。

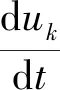
(3.7)

(3.8)

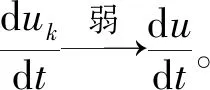
(3.9)

根据参考文献[5]得uk在L2(0,T;H)中弱收敛于u。通过对(3.1)两边同时取极限，由(3.7)、(3.8)和(3.9)可得uk在H,V′中，uk弱收敛于u，∀t∈[0,T]。再通过对(3.1)取极限，

对于∀v∈V∩L2(Ω)，

(f,v)，

因此u满足：

利用参考文献[6]，可得u∈C([0,T];H)通过对(3.1)取极限，让k→∞可得u(x,0)=u0(x)，则定理1得证。