土工格栅加筋陡坡路堤的力学行为分析

郭铭倍，宋玲*，刘杰，段彦福

(1石河子大学水利建筑工程学院,新疆 石河子 832003; 2新疆维吾尔自治区交通规划勘察设计研究院,新疆 乌鲁木齐 830006)

土工格栅具有良好的抗拉和耐腐蚀性能，在土体中铺设土工格栅可以提高土体的抗拉强度，并增强土体结构的整体稳定性。目前，国内外一些学者借助现场试验或室内模型试验以及有限元软件对土工格栅加筋土结构的整体性和稳定性开展了研究。贾敏才等[1]研究表明土工格栅可以限制路堤水平方向的位移，改善土体应力环境，避免路面的不均匀沉降，对路堤有显著的加固作用；Perkins S W和Edens M Q[2]借助数值模拟描述土工格栅加筋土结构的性能，并将该模型的预测结果与一系列的拉拔实验结果进行了比较，结果显示土工格栅的蠕变对土工合成材料的变形影响很小；杨庆等[3]通过室内模型试验发现加筋可以提高路堤边坡的稳定性，限制边坡的侧向位移，提高路堤边坡的承载能力；徐林荣等[4]通过27个加筋土陡边坡模型试验得到多种影响因素下边坡滑裂面的变化规律，探讨了边坡滑裂面的形态，得出可将筋材受力最大点作为筋材断裂点。

借助大型有限元分析软件对土工格栅加筋路堤进行模拟，不仅可以得到土工格栅的受力情况，还可以呈现土工格栅加筋路堤的位移和潜在滑裂面的变化情况，弥补以极限平衡理论为代表的主流设计方法在极限状态下结构物性状掌握不足的问题。文献[3-6]通过模型试验研究对加筋结构体展开了力学行为分析，但这些试验受尺寸效应影响较大，也不可能完全还原施工的真实过程，同时，至今国内专门进行大型土工格栅加筋路堤现场监测的实例也不多，因此，本文基于此在现场监测的基础上结合有限元数值分析，对土工格栅加筋陡坡路堤的整体稳定性进行分析。

1 工程概况

S101线沙湾段公路位于新疆沙湾县境内天山北坡边缘，起于沙湾县S101线K192+400处，途径沙湾县石场镇、西戈壁镇、博尔通古乡和鹿角湾景区，止于S101线K253+420处与省道S223相连。路线全长61.02 km，采用三级公路标准，路基宽度8.5 m，路面宽度7.0 m，路面为沥青混凝土路面，标准轴载为BZZ-100。

K226+600—K226+702段地面横坡较陡且需要收缩坡脚，本文选择其中最高断面K226+640作为监测断面(图1)，其断面高度为10.07 m，路堤边坡坡率1∶0.75。

加筋材料为TGDG80HDPE单向土工格栅，综合折减系数为5，设计容许抗拉强度为16 kN/m，断面格栅布设方式见表1。

图1 K226+600—K226+702段陡坡路堤实体工程Fig.1 Solid engineering of steep slope embankment in section K226+600～K226+702

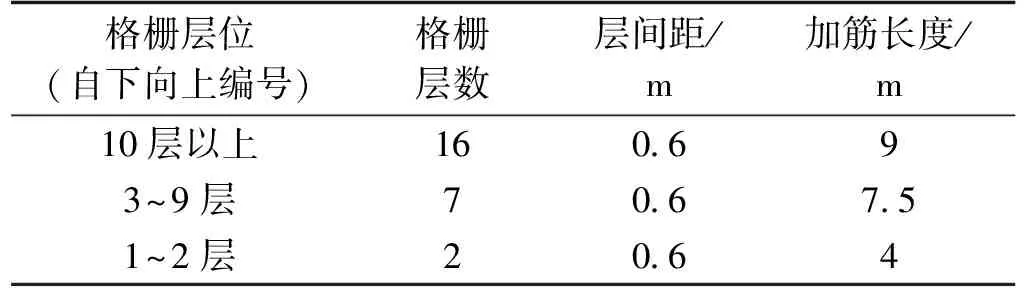
表1 土工格栅层位设计表Tab.1 Geogrid layer design table

在土工格栅上安装柔性位移计，位移计末端通过导线与S101线沙湾段公路建立的远程实时监测系统相连接(图2)，对土工格栅应变数据进行长期监测和收集。

图2 远程监测系统Fig.2 Remote monitoring system

2 数值建模

2.1 模型建立

对监测断面进行有限元数值建模，模型高度为10.07 m，路堤宽度为8.5 m。借助Midas GTS NX有限元分析软件采用三角形加四边形网格划分形式实现路堤的建模，结果如图3所示。

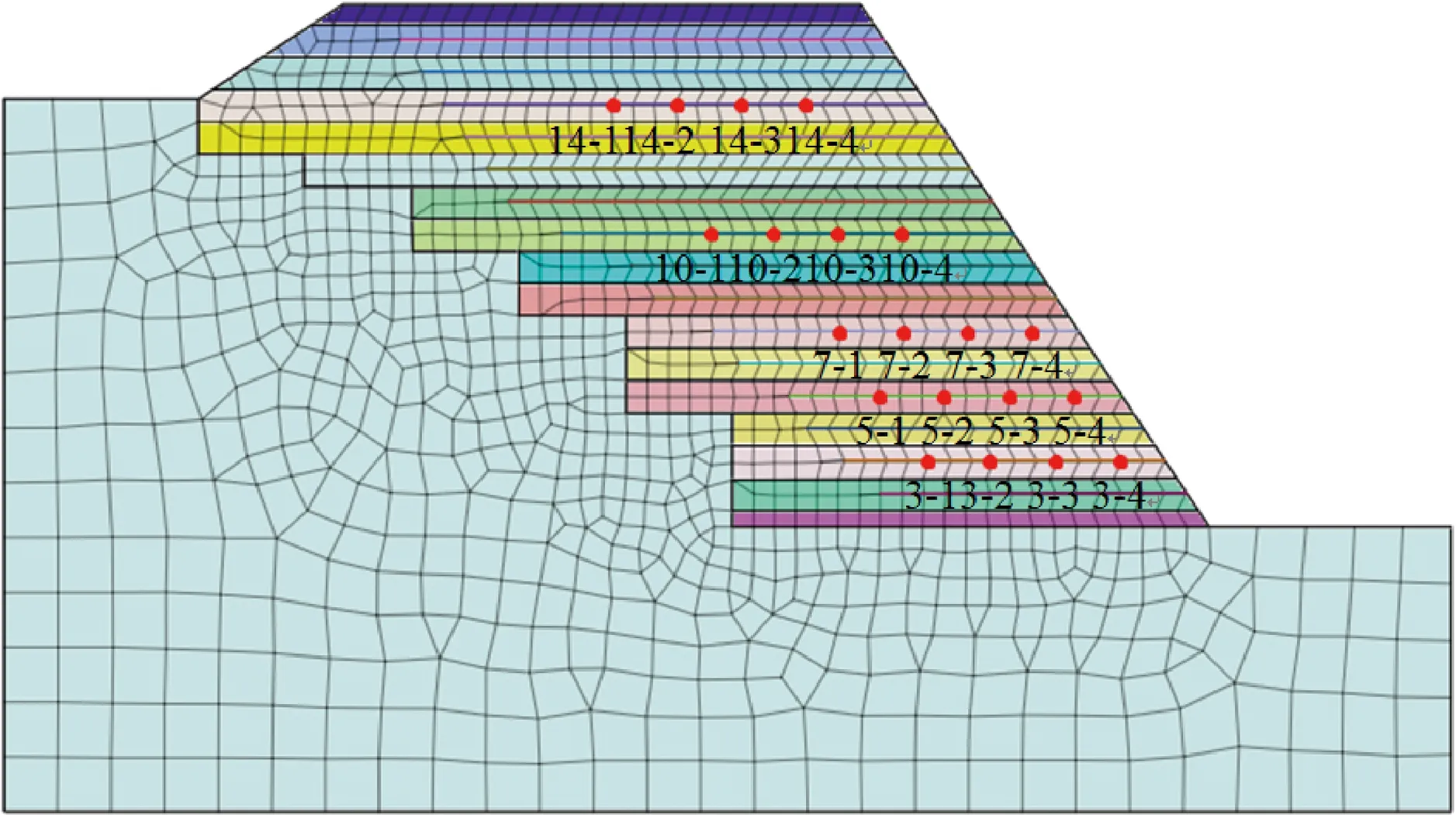
图3 数值模型Fig.3 Numerical model

在数值模型土工格栅单元上设置监测点(图3)，定位监测点与加筋路堤内部柔性位移计埋设点的位置相同，监测点水平间距2 m，其中第3、5、7层土工格栅(自下而上)最右侧的监测点距离边坡50 cm，第10层和14层距离边坡150 cm。

2.2 材料本构关系与参数选取

模拟加筋路堤时，模拟结果由选取的本构模型和计算参数所决定。本文模型的模拟对象分为填土、土工格栅和地基土，其中填土和地基土为粗粒土，根据大型三轴试验结果[7]，本文土的本构关系设置为摩尔-库伦模型；土工格栅在工作状态下应力应变关系位于弹性范围内，根据土工格栅的拉伸试验结果[7]，本文土工格栅的本构关系为弹性模型，模型计算参数见表2。

表2 材料计算参数Tab.2 Material calculation parameter

2.3 建立接触面

采用Midas GTX NX软件内置的goodman单元作为筋土接触单元，其界面接触参数主要有粘聚力、内摩擦角、法向刚度和切向刚度4个参数。土工格栅截面和接触特性参数见表3。

表3 界面接触参数Tab.3 Interface contact parameter

2.4 模拟结果及分析

2.4.1 路堤滑裂面

土工格栅加筋陡坡路堤稳定性分析方法中未考虑填土与土工格栅的协调变形，不能完全反映加筋路堤潜在滑裂面呈现的情况。采用有限元数值模拟进行路堤边坡稳定性的分析，主要通过2种依据进行判断边坡是否处于破坏状态，一种是通过有限元数值计算得到力和位移的突变作为路堤边坡失稳的标志[8-9]，另一种将有限元数值模拟得到从坡脚到坡顶塑性贯通的区域作为路堤边坡失稳的依据[10]。因此，可以通过等效塑性应变的变化得出路堤的潜在滑裂面，也可利用路堤水平位移定量地确定路堤的潜在滑裂面[11]。

由未加筋路堤的塑性应变云图(图4)可以看出：

(1)路堤右侧区域已经出现塑性区贯通，该区域从坡脚位置开始沿着滑弧向上延伸至路堤坡顶；滑裂面呈较陡的圆弧滑动，且离坡面位置很近。

(2)路堤结构已出现破坏现象，特别是坡脚位置破坏最为明显，滑裂面以外位置的塑性应变值很小，有的接近于0，这些区域通常不会发生较大的破坏和变形。

(3)经数值计算得到加筋路堤的稳定性系数为1.15，低于JTG D30—2015《公路路基设计规范》路堤安全系数最小值1.45，表明该路堤结构处于不稳定的状态。

图4 未加筋路堤塑性区分布Fig.4 Plastic zone distribution of unreinforced embankment

图5是土工格栅加筋路堤的塑性应变云图。

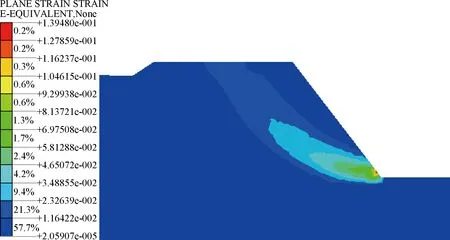
图5 加筋路堤塑性区分布Fig.5 Plastic zone distribution of reinforced embankment

对比图5与图4可知：加筋路堤潜在滑裂面的位置距离边坡更远，路堤塑性贯通区域向路堤内部移动，滑裂面底端已向地基处开始延伸。这与杨庆[3]通过室内小尺寸路堤边坡模型试验研究得到的结论一致。

对比加筋前后的路堤塑性区分布情况可知：与加筋路堤相比，未加筋路堤的塑性区域范围的增幅较大，且未加筋路堤的塑性应变均值较加筋路堤的成倍增加，塑性应变最大值所处的位置几乎没变，但受筋土作用机理的影响减至0.139。此时加筋路堤中土体所提供的下滑力小于路堤边坡的抗滑力，路堤边坡处于状态稳定，主要是由于土工格栅对土体产生水平约束，使得路堤抗滑力增大，整体性增强，由数值计算得到的稳定性系数1.72，说明此时路堤边坡处于稳定状态，土工格栅加筋可显著提高路堤边坡的稳定性。

2.4.2 路堤水平位移

未加土工格栅路堤水平位移云图(图6)显示：路堤边坡沿着坐标轴X的指向(正向)形成一个滑裂面，其中滑裂面顶部位置最大水平位移约为19 cm；路堤水平位移最大值存在于滑裂面坡脚附近位置，其值约为29 cm，坡脚附近位置发生剪切破坏。坡脚附近水平位移值明显大于坡顶，这是由于坡脚受到侧向推挤的作用，加上路堤此时处于不稳定状态，路堤边坡沿着水平方向发生了大幅度滑动。

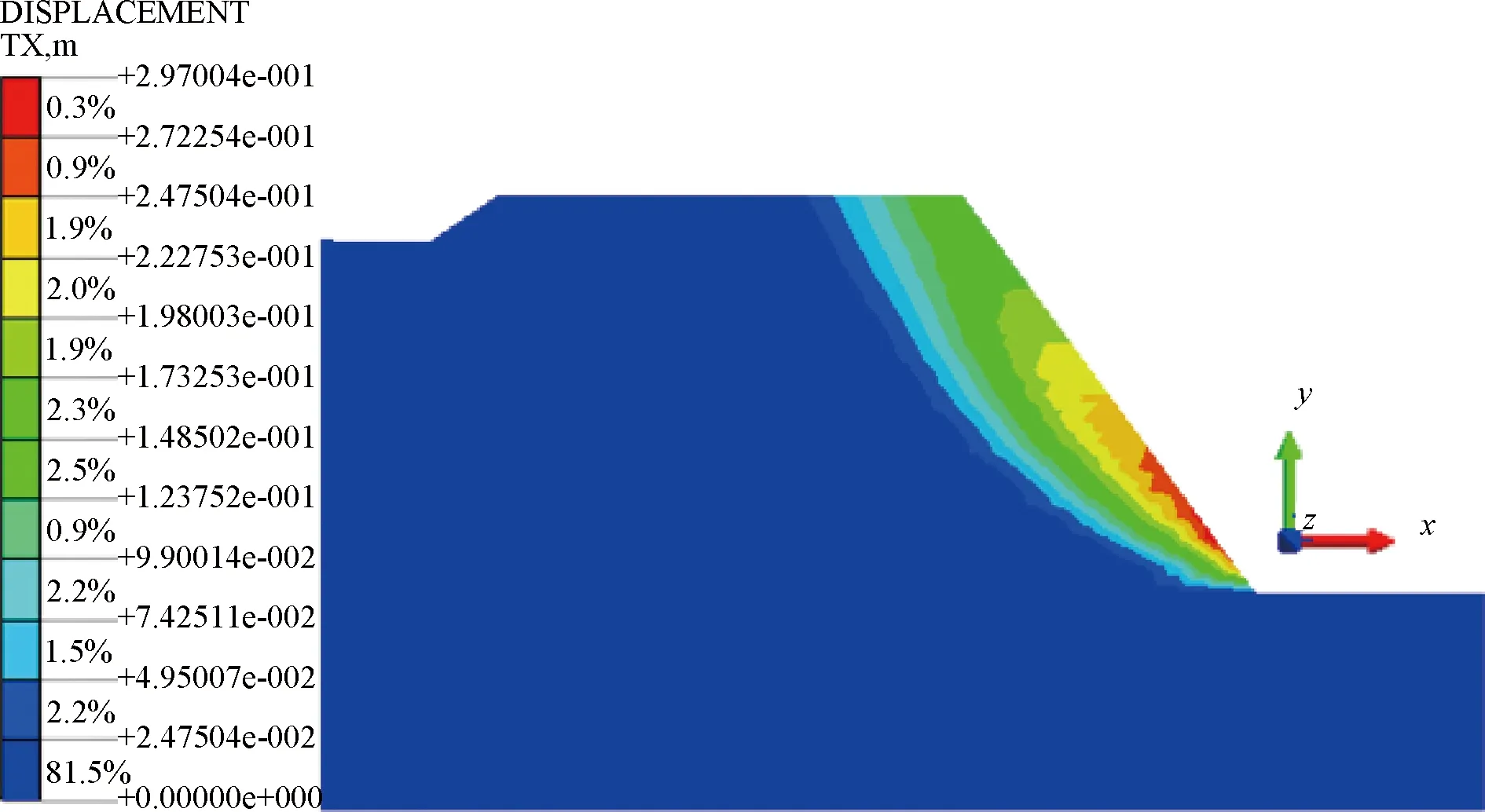
图6 未加筋路堤水平位移Fig.6 Horizontal displacement of unreinforced embankment

图7是加筋路堤水平位移云图。对比图7与图6可知：加筋路堤的潜在滑裂面较未加筋路堤明显向路堤内部后移，加筋前后路堤潜在滑裂面的位置发生了明显变动。

在用极限平衡法判断路堤的滑裂面位置时，通常先对未加筋路堤进行稳定性计算，得出滑动面位置，然后根据滑动面位置进行筋材布置设计，再进行加筋后的稳定性计算。这种方法未考虑加筋前后路堤的滑裂面位置会发生变动，有一定的不合理性,因此，有限元法比极限平衡法更能准确的得出加筋以后路堤滑裂面的位置。

图7显示：

(1)水平位移负值区域主要分布在路堤边坡滑裂面以外区域处。该区域沿着坐标X的负向产生很小位移，其值可以忽略不计，且与右侧路堤边坡滑动方向相反，所以其位移值表示为负数。

(2)路堤加筋前后最大水平位移位置大致相同，加筋区域水平位最大移值约为4.7 cm，相比未加筋区域减少了83.8%，表明加筋可有效限制路堤的水平位移。这主要是由于加筋使土体应力进行了重新分布，土工格栅在承受拉力后，筋材与土体之间的相互作用增大了土体的抗剪强度，使得路堤的整体性增强。

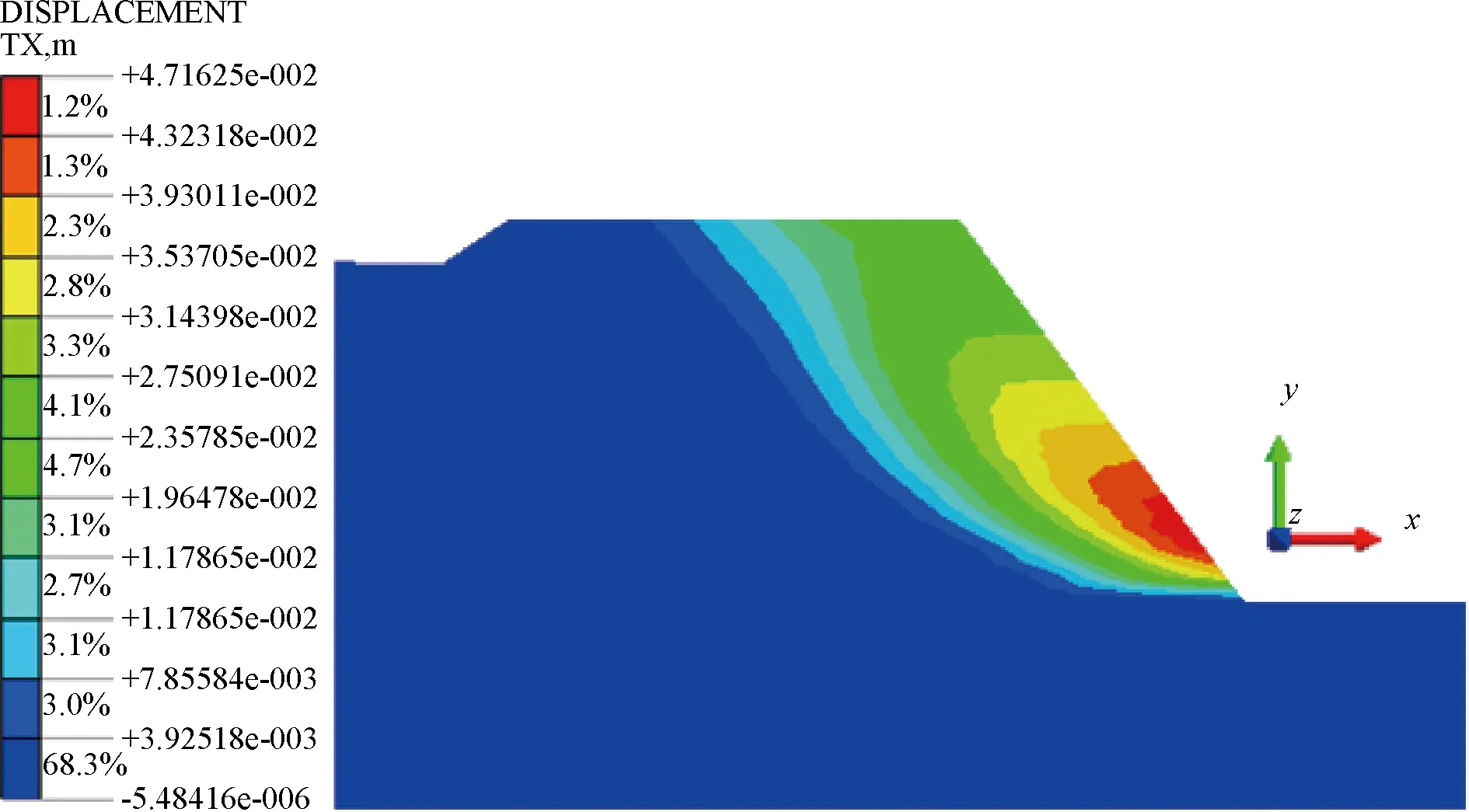
图7 加筋路堤水平位移Fig.7 Horizontal displacement of reinforced embankment

3 土工格栅受力分析

分配加筋路堤的筋材时，利用极限平衡法能计算出土工格栅抗滑力总值，但不能准确得出每层筋材所承受的拉力，涉及到复杂工程，因此，本文采用极限平衡分析与数值计算相结合的办法，寻求合理的加筋结构形式，确定合适的加筋布设方案，深入分析加筋路堤的稳定性。

3.1 数值模拟的应变分析

利用有限元法能直观的分析每层筋材的受力情况。土工格栅受力云图(图8)显示：加筋路堤上部区域筋材所受拉力较小，中部和下部区域所受拉力较大。表明中部和下部区域的土工格栅对路堤稳定性贡献大于上部土工格栅，因此，在设计中应优先采用上疏下密的布筋方式，在采用等间距布筋时，路堤中部和下部应选用较高强度的土工格栅。

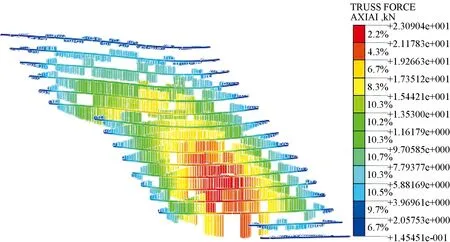
图8 筋材受力Fig.8 The reinforcement material stress

图9显示：路堤边坡滑裂面区域的格栅应变较其它区域数值偏大，土工格栅应变最大值接近1.5%(编号3和4)。已知现场铺设的土工格栅在2%伸长率时的拉伸强度为25.8 kN/m，推算出筋材所受最大拉力为19.35 kN/m，这仅为所用筋材极限抗拉强度值的24.18%，说明格栅受力与极限值仍相差较远，土工格栅未达到破坏的状态。路堤边坡潜在滑裂面的出现使土体的受力状态发生改变，土工格栅可以平衡土体的受力，同时也可以限制路堤边坡的水平位移，因此，滑裂面区域的土工格栅受力较大，格栅应变大于其它部位应变值。

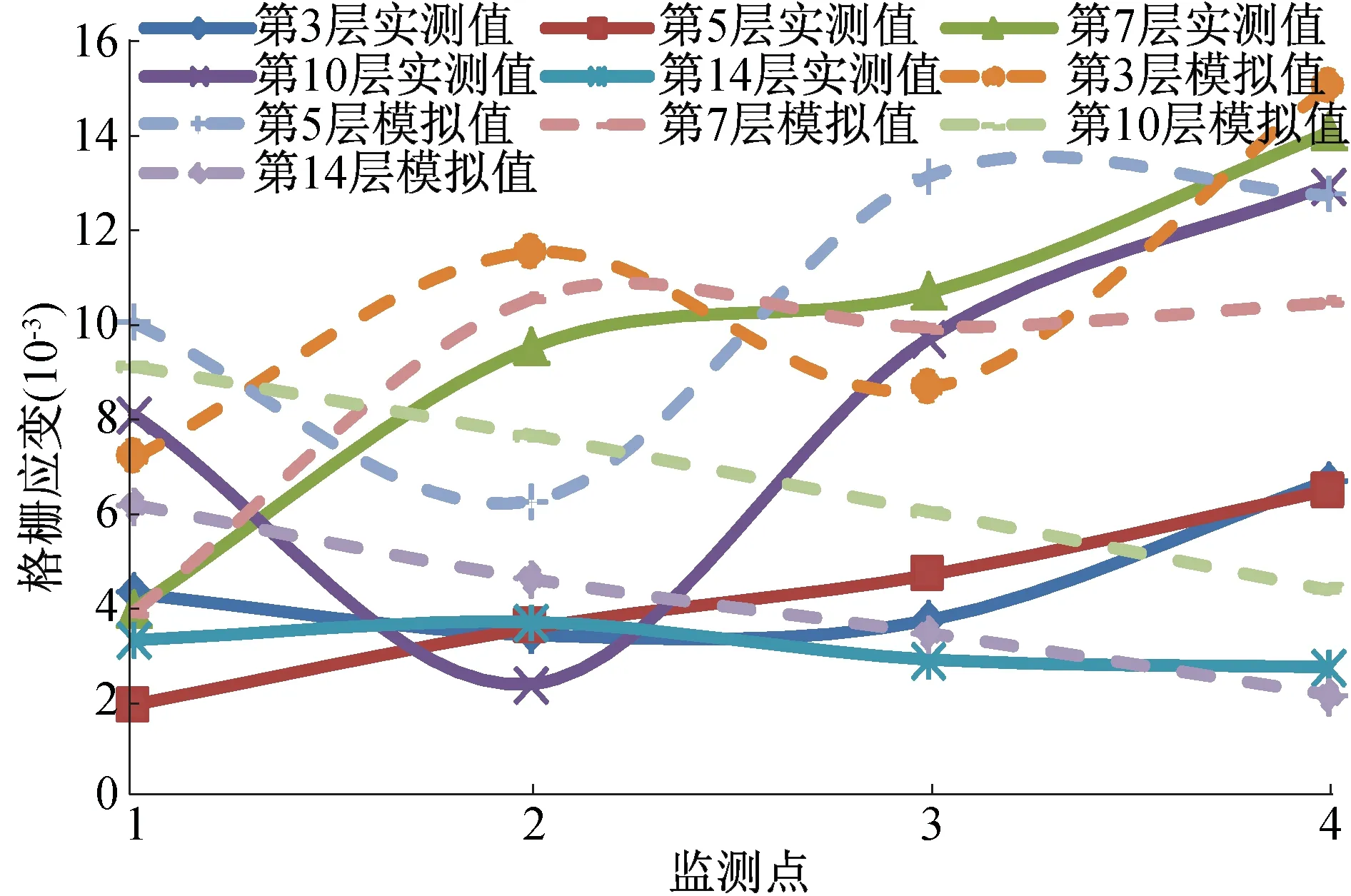
图9 模拟与实测应变对比Fig.9 Comparison of simulated and measured strain

3.2 实时监测的应变分析

选取施工完毕后第45天格栅应变实测数据进行分析，实测得到的土工格栅应变均为正值，说明所测位置的土工格栅均为受拉。所测7-4点的应变最大，仅为1.4%，该点所受拉力为18.0 kN/m，与设计值基本相同，说明设计方案合理。现场监测结果(图9)表明：

(1)不同层位的土工格栅应变值并不相同，路堤中部和下部位置应变值较大，而路堤上部区域的筋材应变值较小。

(2)实测应变最大值仅为筋材极限抗拉强度的22.5%。设计时通常将土工格栅的蠕变、施工损伤和老化因素考虑在内，利用折减系数对土工格栅强度进行折减。与现有蠕变试验[2]、施工损伤[12]和老化试验资料[13]对比分析后可知：土工格栅所受拉力较小时发生的蠕变变形很小；土工格栅施工损伤主要受路堤填料的影响；HDPE土工格栅受老化性能影响在较长一段时间内其拉伸强度仍变化不大。这充分表明现行规范中所采用的折减系数较为保守。

3.3 实测与模拟对比

模拟与实测得到的各层格栅应变分布对比结果(图9)表明：

(1)实测与模拟得到的土工格栅受力规律大致相同，但加筋路堤内部受力情况不尽相同，主要是由于加筋体上部承受重力作用较小，重力作用主要传达至中部和下部区域，中部和下部区域成为加筋路堤主要的受力区。

(2)每层格栅不同部位的应变分布不同，且各层格栅的应变分布规律也有所差别，其中，第3、5、7、10层格栅应变自路堤坡面至内部水平方向整体逐渐减小，第14层格栅由于靠近顶层且受荷载影响较小，其层位不同位置应变值差别不大。

(3)各层筋材应变最大值主要分布在滑裂面位置，路堤中部和距离路堤边坡较远处的格栅应变较小，这与Bathurst[14]通过试验得出结论较为一致。分析其原因主要是，路堤边坡会产生侧向位移，土工格栅发挥加筋锚固作用限制土体的滑动，此时边坡滑裂面位置的格栅受力最大，因此该部位的筋材应变最大，各层格栅应变最大点连起来形成滑裂面的形状。

(4)与模拟计算值相比，第3和第5层格栅应变的监测值较小，这与冯晓静[15]通过路堤现场试验研究所得的结论较为接近。这是因为底层格栅由于离地基较近，地基的摩擦限制作用对其产生了影响。

(5)由于加筋机理的复杂性，实测值与模拟计算值存在一定的差异，但是通过数值模拟能够大体得出路堤内部筋材受力的规律，这可为优化设计的方案提供一定的依据。

4 结论与建议

(1)可通过数值模拟云图中路堤等效塑性应变的变化和水平位移数值确定路堤潜在滑裂面的位置。

(2)加筋使路堤滑裂面向内部移动，最大水平位移减少83.8%，说明加筋可显著增强路堤的稳定性。

(3)路堤下部格栅受力明显大于上部。在实际设计中应优先采用上疏下密的布筋方式，等间距铺设土工格栅层，可考虑在中部和下部区域铺设高强度的筋材。

(4)筋材的数值模拟计算值与实测值有差异，但整体符合路堤格栅受力特点。路堤滑裂面位置的筋材应变值为该层格栅应变最大值，筋材受力最大值仅为极限抗拉强度的24.18%，说明格栅受力有较大的富余度，从经济性角度出发，在实际设计中应避免过于保守。