统计解题中的误区与警示

■王 飞 刘大鸣(特级教师)

本文针对统计解题中常见的易错、易混、易忘的典型问题进行错解剖析,帮助同学们识破命题者精心设计的陷阱,希望对同学们的学习有所帮助。

误区1：对系统抽样的特点理解不准确

例1中央电视台动画城节目为了对本周的热心观众给予奖励,要从2014名小观众中抽取50名幸运小观众。先用简单随机抽样从2014人中剔除14人,剩下的2000人再按系统抽样方法抽取50人,则在2014人中,每个人被抽取的可能性( )。

A.均不相等

B.不全相等

错解：应选A或D。

剖析：对个体入样的可能性与抽样间隔理解不透,导致错选。对于A,认为剔除14人,被抽取的机会就不相等了。对于D,认为被抽取的机会相等,计算时利用了剔除后的数据。

正解：在系统抽样中,若所给的总体个数不能被样本容量整除,则应先剔除几个个体。本题先剔除14人,然后再分组,在剔除过程中,每个个体被剔除的机会相等,所以每个个体被抽到的机会都相等,均为应选C。

警示：当总体容量较大,总体可以分为均匀的几个部分时,用系统抽样较为合理;当总体容量除以样本容量不是整数时,要先在总体中剔除部分个体,总体中的每个个体被剔除的机会是均等的,也就是说每个个体不被剔除的机会也是均等的。由此可知在整个抽样过程中,每个个体被抽到的机会仍然相等。设在第一段内用简单随机抽样方法确定的个体编号为a1,按系统抽样法,则抽取样本an满足

误区2：忽视分层抽样的特征

例2某单位有老年人28人,中年人54人,青年人81人,为了调查他们的身体情况,需从中抽取一个容量为36的样本,则适合的抽样方法是( )。

A.简单随机抽样

B.系统抽样

C.直接运用分层抽样

D.先从老年人中剔除1人,再用分层抽样

错解：因为总体由差异明显的三部分组成,所以考虑用分层抽样。总人数为28+54+81=163,样本容量为36,抽样比为这时无法得到整数解,因此考虑先剔除1人,则抽样比变为若从老年人中随机地剔除1人,则老年人应抽取27×6(人),中年人应抽取54×12(人),青年人应抽取81×=18(人),即组成容量为36的样本。应选D。

剖析：若用简单随机抽样先从老年人中剔除1人,则老年人被抽到的概率显然比其他人群小了,这不符合随机抽样的特征,即每个个体入样的概率相等。注意“先从老年人中剔除1人”与“从总体中随机剔除1人”是不一样的。

正解：直接运用分层抽样法。老年人,中年人和青年人中应抽取的人数分别为

警示：当总体可以分层,层与层之间有明显差异时,选用分层抽样,确定抽样比k是分层抽样的关键。一般地,先确定抽样比k=为总体容量,n为样本容量),再按抽样比k在各层中抽取个体,就能确保抽样的公平性。在每层抽样时,应采用简单随机抽样或系统抽样的方法。

误区3：利用频率分布直方图求频率时忽视组距

例3有一容量为500的样本,把数据分成7组,它的频率分布直方图如图1所示。

图1

根据频率分布直方图,请你估计数据落在[15.5,24.5)内的样本数量。

错解：由频率分布直方图可知,数据落在[15.5,18.5)内的频率为0.054,数据落在[18.5,21.5)内的频率为0.06,数据落在[21.5,24.5)内的频率为0.075。所以数据落在[15.5,24.5)内的样本数量为500×(0.054+0.06+0.075)=94.5。所以估计数据落在[15.5,24.5)内的样本数量大约为95。

剖析：没有看懂纵坐标所表示的意义,错把纵坐标表示的数据作为频率了,其实纵坐标表示的是若要计算频率,则要找出组距,从横坐标中明显看出组距为3。

正解：由频率分布直方图可知,数据分成7组,其组距为3,所以数据落在[15.5,18.5)内的频率为0.054×3,数据落在[18.5,21.5)内的频率为0.06×3,数据落在[21.5,24.5)内的频率为0.075×3。所以数据落在[15.5,24.5)内的样本数量为500×(0.054×3+0.06×3+0.075×3)=283.5。

所以估计数据落在[15.5,24.5)内的样本数量大约为284。

警示：正确地认识频率分布直方图：纵坐标表示的是而非频率;频率=;小矩形的面积=频率。利用频率分布直方图可求众数,中位数和平均数：最高小矩形底边中点的横坐标即是众数;中位数左边和右边的小矩形的面积之和是相等的;平均数是频率分布直方图的“重心”,平均数等于频率分布直方图中每个小矩形的面积乘以小矩形底边中点的横坐标之和。

误区4：对茎叶图的画法规则及特征认识不到位

例4某市对上下班情况作了抽样调查,上下班时间各抽测了12辆机动车的车速如下(单位：km/h)：

上班时间：30,33,18,27,32,40,26,28,21,28,35,20;

下班时间：27,19,32,29,36,29,30,22,25,16,17,30。

用茎叶图表示以上数据。

错解：机动车行驶速度的茎叶图如图2所示。

图2

剖析：对茎叶图画法规则和特征理解不到位,茎叶图中重复出现的数据要重复记录。上述解法漏掉了3个重复的数据。

正解：画茎叶图时,需要将每个数据分为“茎”和“叶”两部分,表示“茎”的数字按照大小顺序由上到下排列,表示“叶”的数字,重复出现的数据要重复记录。

画出茎叶图,如图3所示。

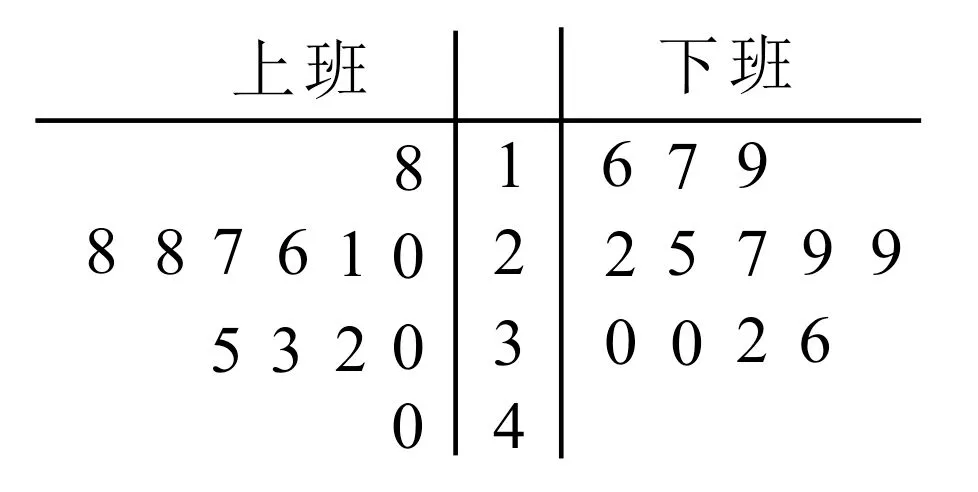
图3

警示：用茎叶图分析数据直观、清晰,所有信息都可以从茎叶图中得到。茎叶图在样本数据较少,较为集中且位数不多时比较适用。由于它较好地保留了原始数据,所以可用来分析样本数据的一些数字特征,如众数、中位数、平均数等。

误区5：忽视方差的统计意义

例5甲、乙两种冬小麦试验品种连续5年的平均单位面积产量如表1所示(单位：t/km2)。

表1

若某村要从中引进一种冬小麦大量种植,请给出你的建议。

错解：由表1中的数据可得=10,则甲、乙两种冬小麦的平均产量都等于10,所以可以引进两种冬小麦的任意一种。

剖析：上述解法只对两种冬小麦的平均产量进行了比较,而忽视了对冬小麦产量稳定性的讨论。

正解：由表1中的数据可得(10.1-10)2+(10-10)2+(10.2-10)2]=(10.8-10)2+(9.7-10)2+(9.8-10)2]=0.244。由于甲、乙两种冬小麦的平均产量都等于10,且s2甲＜s2乙,所以产量比较稳定的为甲种冬小麦,应推荐引进甲种冬小麦大量种植。

警示：平均数反映的是样本个体的平均水平,方差和标准差则反映了样本的波动、离散程度。对于形如“谁发挥更好、谁更稳定、谁更优秀”之类的题目,除了比较数据的平均数,还应比较方差或标准差的大小,以作出更为公正合理的判断。

误区6：运用数字特征作评价时考虑不周

例6一次数学知识竞赛中,两组学生的成绩如表2所示。

表2

经计算,已知两个组的平均分都是80分,请根据所学过的统计知识,进一步判断这次竞赛中哪个组更优秀,并说明理由。

错解：由于乙组90分以上的人数为24,甲组90分以上的人数为20,所以乙组更优秀。

剖析：对一组数据进行分析时,应从平均数,众数,中位数,方差,极差等多个角度进行分析和判断。

正解：(1)甲组成绩的众数为90,乙组成绩的众数为70,从成绩的众数这一角度看,甲组成绩好些。

因为s2甲＜s2乙,所以甲组的成绩比乙组的成绩更稳定。

(3)甲、乙两组成绩的中位数、平均数都是80,其中甲组成绩在80分以上(含80分)的有33人,乙组成绩在80分以上(含80分)的有26人,从这一角度看,甲组的成绩总体较好。

(4)从成绩统计表看,甲组成绩大于或等于90分的有20人,乙组成绩大于或等于90分的有24人,可知乙组成绩在高分段的人数多,同时,乙组满分比甲组多6人,从这一角度看,乙组成绩较好。

警示：正确解答此题,首先,要抓住问题的关键,全方位地进行计算,不能仅从平均数与样本方差的大小去判断哪一组的优劣,对于这样的实际问题,要从实际的角度去分析,如本题中的“高分段人数”“满分人数”等;其次,要在恰当地评估后,作出正确的结论。