估算带“[]”无理数的值
何德海
利用计算器得出含根号无理数近似值的方法相信大家都掌握了,但如果我们手头没有计算器或不允许使用计算器时,该如何估算它们的近似值或大致范围呢?下面结合有关题目谈谈帶“[]”无理数的值的估算方法。
一、采用夹逼法
例1 (2018·台州)估计[7]+1的值在( )。
A.2和3之间 B.3和4之间
C.4和5之间 D.5和6之间
解:∵22=4,32=9,∴[4]=2,[9]=3,
又∵4<7<9,∴[4<7<9]。
即[2<7<3],∴[3<7+1<4]。
故选B。
点评:本题主要考查估算无理数[7]的整数部分。采用“夹逼法”,利用“若a、b都为正数,且a>b,则[a>b]”的结论,可以得出[7]的整数部分。本题对[7]的近似值要求不高,运用一次“夹逼法”,即可求解。
例2 填空:[7≈] (精确到十分位)。
解:∵2=[4<7<9=3],∴无理数[7]的值介于2和3之间,即[7]的整数部分为2。
又∵2.62=6.76,2.72=7.29,∴2.6[<7][<2.7]。又∵2.642=6.9696,2.652=7.0225,∴2.64[<7][<2.65]。∴[7]的百分位上的数为4,根据四舍五入法则,[7≈]2.6(精确到十分位)。
点评:本题仍然是估算无理数[7]的值,但要求精确到十分位,精度要求高了,需要多次运用“夹逼法”。用此种方法,先确定整数位,再确定十分位、百分位等,多次运用还可以求出更加精确的值。此种方法,也适用于其他带根号无理数的估值。
二、利用数轴上的点
例3 (2019·武威)下列整数中,与[10]最接近的整数是( )。
A.3 B.4 C.5 D.6
分析:本题除了运用例1所提供的“夹逼法”外,也可以将教材中提供的“在数轴上画出表示[2]的点”的方法“移植”过来。
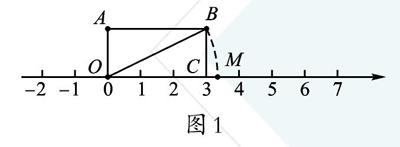
解:如图1,在数轴上,构造边长分别为3和1的长方形OABC(或两直角边分别为3、1的Rt△OCB),然后以O为圆心,以OB长为半径画弧,交数轴的正半轴为M,则点M即为数轴上表示无理数[10]的点,由图可直观看出与[10]最接近的整数是3。本题选A。
图1
点评:本题利用数轴,构造图形,在数轴上直观表示出带根号的无理数,利用图形直观,可估算出该无理数的值。当我们将数轴上的刻度细分时,估值的精度还能有所提高。
(作者单位:江苏省句容市教师发展中心)

