缸盖材料P-S-N曲线测试及疲劳模型选用方法

程祥军，黄国龙，魏涛，孟凡栋，赵立普

(1.内燃机可靠性国家重点试验室，山东 潍坊 261061；2.潍柴动力股份有限公司，山东 潍坊 261061)

缸盖是发动机重要核心零部件之一，用来密封气缸的上部，与活塞顶及气缸壁共同组成燃烧室。其上通常还要布置进排气道、机油孔道和配气机构零件等，结构形状十分复杂。产品开发过程十分注重缸盖的疲劳可靠性设计，P-S-N曲线是构件疲劳可靠性设计和寿命预测的重要基础。基于准确的P-S-N曲线，在产品设计阶段就可准确评估构件可靠性，及时规避风险。从缸盖本体取样进行疲劳试验，是最准确和节省时间、费用的方法，便于工程应用。在进行疲劳试验数据处理时要用到两类模型：一是描述给定应力下寿命或给定寿命下强度的概率分布模型，基于此模型可计算不同存活率的安全寿命；另一个是描述应力与寿命关系的模型，即S-N曲线，基于此模型可计算不同应力下的寿命。目前工程应用上疲劳寿命分布模型基本都采用对数正态分布模型，而S-N应力寿命模型都采用指数函数模型，模型选用单一，而这两类模型分别选用不同的模型都会影响最终数据的准确度。本研究基于缸盖材料特性，提出在处理疲劳寿命分布时不采用单一的分布模型，而是混合不同模型进行处理，并基于此估计安全疲劳寿命。通过对比分析验证了不同应力寿命S-N模型数据处理偏差，为缸盖疲劳可靠性设计提供了更加准确的材料疲劳数据处理方法。

1 试验材料及数据

以HT280缸盖为研究对象，其材料化学成分见表1。在缸盖火力面纵向取样(见图1)，试样形状及尺寸见图2。先进行常规拉伸试验，参照GB/T 228.1—2010《金属材料 拉伸试验 第1部分：室温试验方法》。测试仪器为Zwick250电子万能拉伸试验机，拉伸速度为2 MPa/s，试验结果见表2。

表1 HT280材料化学成分(质量分数) %

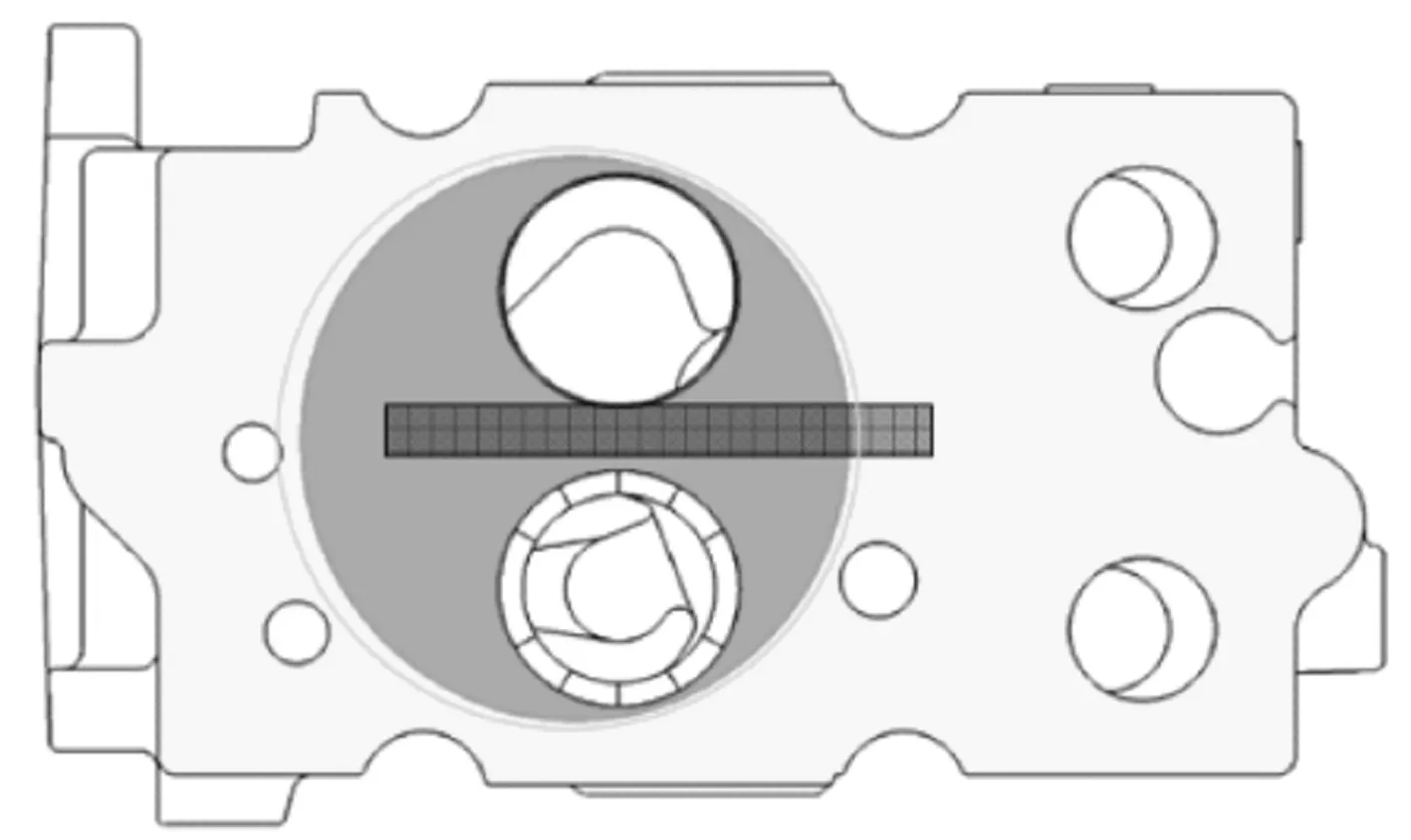
图1 取样位置

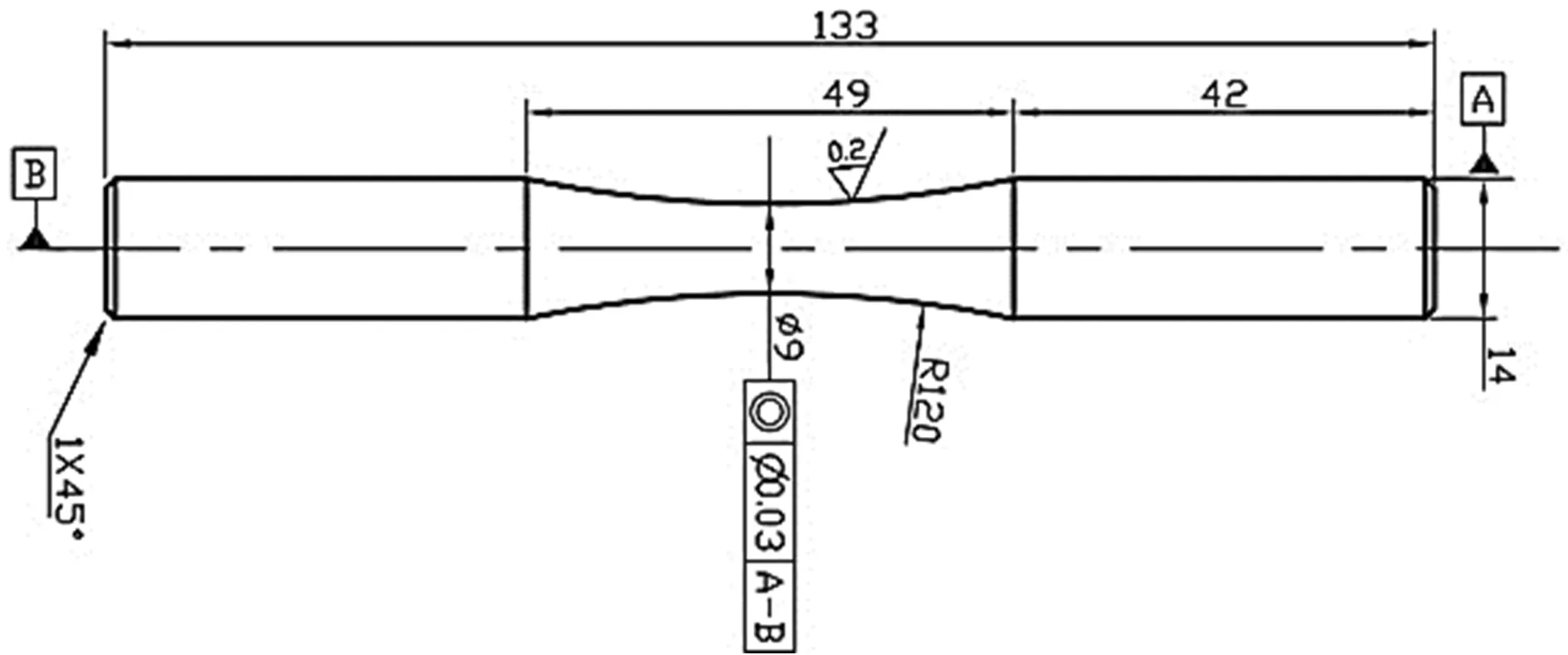
图2 疲劳试样示意

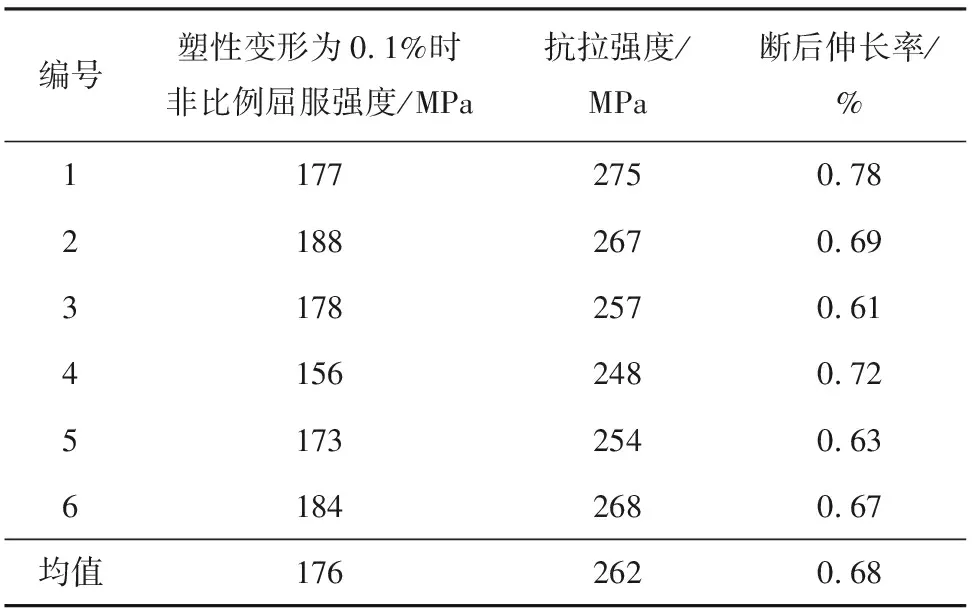
编号塑性变形为0.1%时非比例屈服强度/MPa抗拉强度/MPa断后伸长率/%11772750.7821882670.6931782570.6141562480.7251732540.6361842680.67均值1762620.68

疲劳试验参照GB/T 3075—2008《金属材料疲劳试验轴向力控制方法》，试验仪器为Instron8801。应力比R=-1，频率20 Hz，加载波形为正玄波。

采用升降法测试疲劳极限，低于疲劳极限认为材料不会产生损伤，即无限寿命，循环基数为107，初始载荷为85 MPa，应力增量为5 MPa。若当前应力水平下产生了破坏，则降一级试验，越出则增一级试验，要求试验至少保证6对有效数据。

有限寿命采用成组法测试，分130，120，110，100 MPa四级应力水平，每个应力水平至少5个试样，确保样本数满足概率统计分析需求，可以分析计算各存活率的安全寿命。成组法疲劳试验数据见表3。

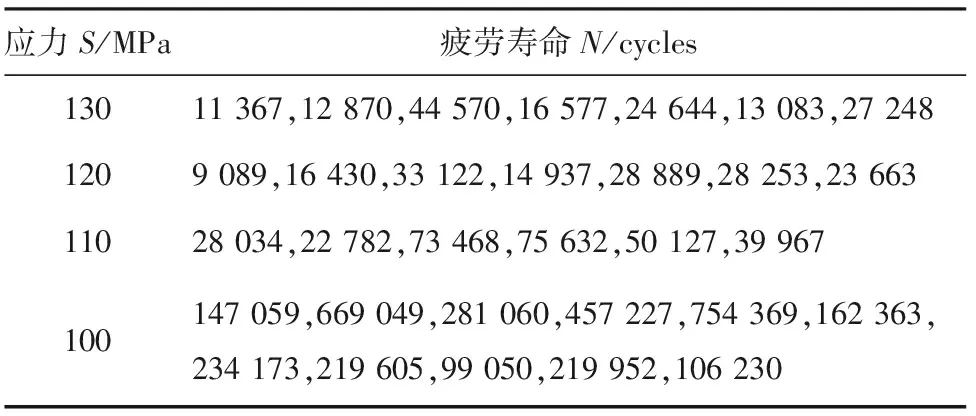
表3 HT280材料成组法疲劳试验数据

2 疲劳寿命分布模型选用及参数计算方法

给定应力下的疲劳寿命被认为是一自由变量，研究表明有两种分布函数最能准确描述：对数正态分布和三参数威布尔分布[1-7]。目前行业标准、国家标准里的处理方法均是采用正态分布。

2.1 存活率的确定方法

对于满足某一概率分布类型的疲劳试验，以随机抽样的方式抽取一个样本容量为n的子样，将子样的试验值按从小到大的顺序依次排列：

x1(i=1,2,3,…n)。

(1)

对于概率分布类型的存活率可用平均秩或中位秩2种方法来计算。当疲劳数据样本较小时，一般采用中位秩的方法来求存活率，中位秩的结果比平均秩的结果准确。用中位秩计算存活率的公式如下[8-9]：

(2)

此存活率与疲劳寿命累计概率密度函数f(x)(即疲劳失效率)之和为1。

2.2 对数正态分布及参数计算

当给定应力下疲劳寿命的对数呈正态分布时，

(3)

式中：x=logN；μ和σ分别是x的均值和标准差。此式给出了对数寿命失效的累计概率，即总样本在小于或等于x下的失效比例。但没有考虑在疲劳极限处或附近发生失效的概率，这一区域，一些试样可能失效，而其他试样也可能不失效，分布的形状经常是不对称的，此时正态分布已不太适合。对于某一应力水平下不同存活率安全寿命的估算，先采用中位秩方法计算样本存活率或失效率，将失效率转换成对应的标准正态偏量，再用最小二乘法拟合标准正态偏量与对数寿命，根据线性拟合相关系数评价拟合效果并求解不同存活率的安全寿命。

2.3 三参数威布尔分布及参数计算

威布尔分布的优点是存在最小安全寿命，即100%存活率的安全寿命。而按正态分布理论，只有当对数寿命logN趋于-∞，即N=0时，存活率才等于100%，显然这不符合实际情况。威布尔分布可以很好地弥补这一不足，其频率函数为

(4)

式中：N0为最小寿命参数；Na为特征寿命参数；b为威布尔形状参数。为计算这3个参数，将上式进行对数转换：

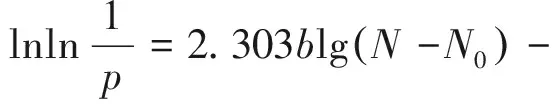
(5)

式中：p为存活率，p=1-f(N)。令y=lnln(1/p),x=lg(N-N0)，计算y与x的线性相关系数Rxy，显然Rxy随N0取值不同而不同，求解的N0应使得Rxy绝对值最大，即线性相关性最大。本文利用Matlab编程，采用迭代法计算N0。求解N0后再利用最小二乘法拟合求解b和Na。

2.4 寿命分布模型选用方法

大量研究表明，在长寿命区正态分布符合性较差，而威布尔分布符合性较好，此时再按正态分布很难获得准确的结果。但正态分布在中短寿命符合性好，且较威布尔分布数据处理简单。因此，本研究充分考虑分布模型的影响，根据不同的应力水平选用合适的分布模型，在高应力中短寿命区105～106选用正态分布模型，数据处理简单快捷； 在低应力高寿命区106及以上选用威布尔分布模型，使数据处理更加精准。这种混合采用两种寿命分布模型的数据处理方法既保证数据处理相对简单快捷，又提高了精度。

对于130，120，110 MPa 3个应力水平寿命分布模型选用对数正态分布，而100 MPa应力水平选用三参数威布尔分布。根据给出的计算方法，计算各应力下寿命分布模型公式及不同存活率安全寿命，结果见表4。

表4 不同应力水平疲劳寿命分布模型公式及安全寿命计算值

3 S-N模型选用及参数计算方法

目前，在疲劳设计和疲劳性能测试上有3种典型的S-N曲线模型[10-15]：

emSN=C(指数函数模型)，

(6)

SmN=C(幂函数模型)，

(7)

(S-C)m=D(三参数幂函数模型)。

(8)

式中：S为应力幅或最大应力，本试验应力比R=-1，应力幅和最大应力相等，因此模型中S均指应力幅；m，D均为材料常数，与材料性质、试件形式和加载方式等有关；C为理论应力疲劳极限。工程上多用前两个模型，主要是前两种模型数据处理相对简单。三参数模型数据处理及参数计算较为复杂，但拟合预测更加准确。本研究三参数模型的计算方法如下：将式(8)两边取对数，则lgN与lg(S-C)呈线性关系，两者的线性相关系数随C值变化，求解C值使得两者线性相关系数最大，再用最小二乘法拟合求解m和D。C值的计算采用Matlab编程，程序如下：

Y=[logN1;logN2;logN3;...];各级对数寿命均值

S=[S1;S2;S3;...];各级应力水平

C=1:0.01:min(S)-1; 给定C值范围

X=log10(S-C);

for i=1:length(C)

R=corrcoef(Y,X(:,i));

RR(i)=abs(R(2));

end

max(RR);计算相关系数最大值

n=find(RR==max(RR));找出最大相关系下标

C=C(n);输出C值

根据计算的各应力水平下不同存活率的安全寿命，进行P-S-N曲线的绘制。如上所述，针对3种S-N曲线模型，用50%存活率的数据分析了3种疲劳应力寿命模型预测偏差，偏差定义为

(9)

3种S-N模型预测偏差见图3，可见三参数模型预测准确度明显优于另两种，预测最大偏差仅为±1.8%，其他两种约±5%。

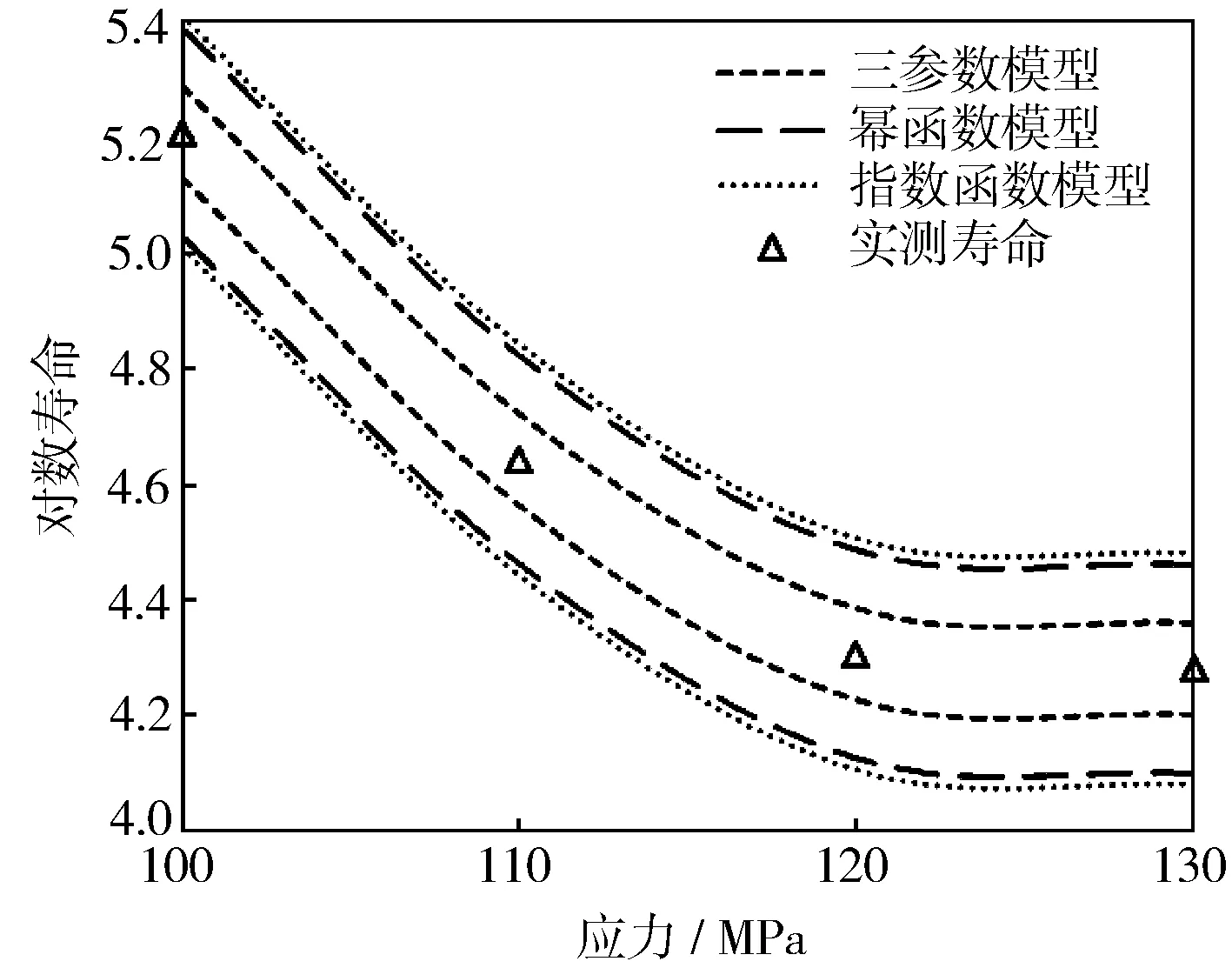
图3 不同S-N模型预测偏差

4 P-S-N曲线

一条完整的S-N曲线应包括低寿命区、中寿命区、长寿命区，用一个模型完整地表达这3个区域是很困难的。本研究中介绍的3个模型主要用于中长寿命区，在接近107寿命区其适应性稍差，因此在处理S-N曲线时，斜线段和水平段之间通常采用圆弧过渡。

疲劳升降图见图4，共7对有效数据，按HB/Z112标准处理数据，标准差为5.27 MPa，50%存活率疲劳强度为81.94 MPa，约为抗拉强度的0.3倍，90%存活率疲劳强度为74.98 MPa。采用3种寿命分布模型计算50%存活率寿命，根据结果拟合预测疲劳强度，结果见图5。

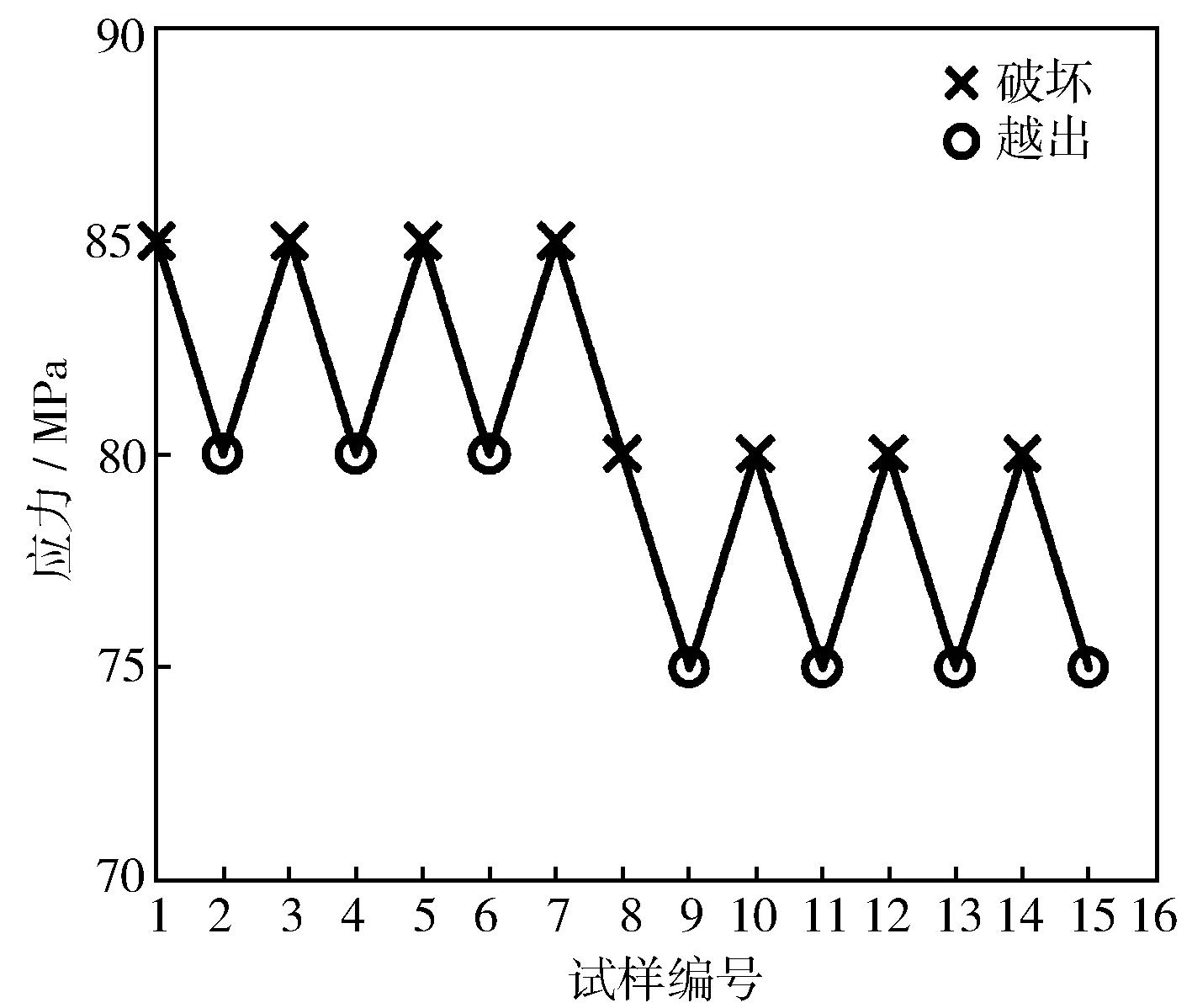
图4 HT280疲劳升降图

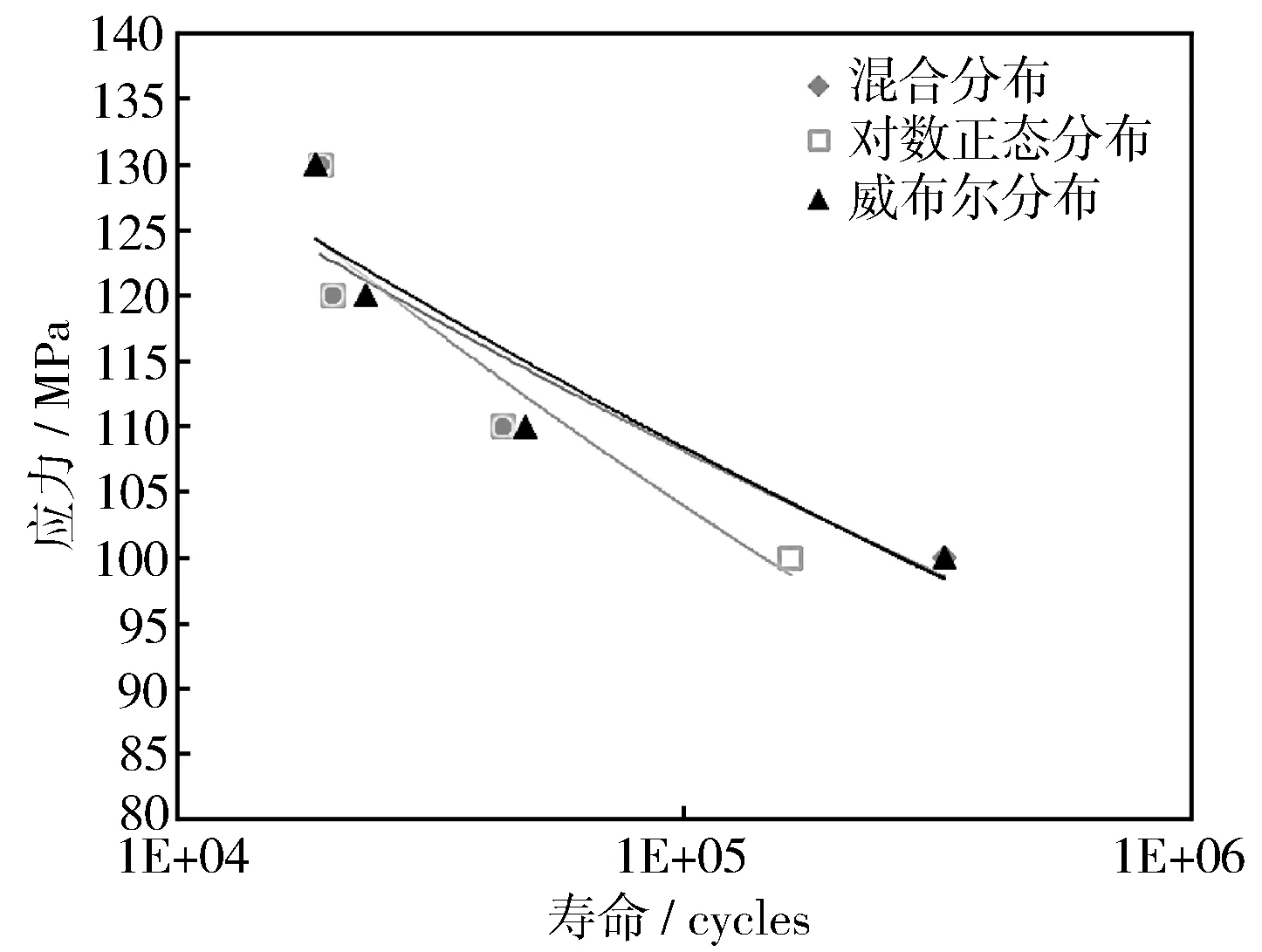
图5 HT280材料P-S-N曲线

对数正态分布在低寿命区与威布尔分布相近，但在中长寿命区相差较大，混合分布、威布尔分布、对数正态分布拟合预测的50%疲劳强度分别为75.9，74.1，63.7 MPa。与升降法测试结果的偏差分别为6，8，18 MPa，混合分布偏差最小，说明混合分布方法能快捷、准确地处理数据。

5 结论

a) 采用升降法和成组法测试缸盖本体材料疲劳性能，指定107的50%和90%存活率疲劳强度分别为81.94 MPa，74.98 MPa，标准差为5.270 5 MPa；

b) 提出了一种新的疲劳寿命分布选用方法，高应力低寿命区选用对数正态分布模型，低应力长寿命区选用三参数威布尔分布模型，并给出了参数计算方法；

c) 分析了3种疲劳应力寿命模型预测缸盖材料疲劳寿命的准确度，结果表明，三参数模型预测精度明显优于另外两种，预测最大偏差仅为1.8%；

d) 基于寿命分布和应力寿命模型选用方法，拟合预测50%疲劳强度。混合寿命分布拟合预测的疲劳强度与升降法测试结果的偏差最小，为6 MPa，说明此方法可以快捷、准确处理数据。