基于ASBCS算法的混合Copula邻近水文站年径流量预测
佘纬,安智,田莎莎,张相来
(1 中南民族大学 数学与统计学学院,武汉430074;2 中南民族大学 计算机科学学院,武汉430074)
径流是陆地上水量最直观的反映,为了能够更好地利用和保护水资源,我们不仅要了解径流的长期变化规律,还要做好径流的预测工作,来指导人们的生产和生活[1,2].由于地理位置偏僻或者自然灾害,有时会出现水文站水文数据缺失的现象,这就需要我们能够根据邻近站点的水文数据来预测出缺失水文站的水文数据.由于水文环境和水文现象的复杂性,单变量的水文分析已经不能满足工程设计和人们生产生活的需要,在进行水文分析时,往往会涉及到多个参数,而Copula函数的优点正是可以描述变量间的相关性,而且可以通过连接每个变量的边缘分布,得到这些变量的联合分布函数.因此,Copula函数得到了水文学家的青睐,越来越多的用于水文学的相关分析和预测问题中.近年来很多学者将Copula函数应用于多变量水文频率分析中[3,4].2007年,《Journal of Hydrologic Engineering》杂志对Copula函数在水文学中的应用进行了专刊介绍[5-7].SONG利用三变量Plackett copula函数模拟了干旱持续时间、严重程度和到达时间的联合概率分布,结果表明Plackett copula能够产生相关干旱变量的双变量和三变量概率分布[8].CHEN采用多变量Copula方法对干旱期进行量化,以中国汉江上游流域为例,研究了各干旱状态下的依赖结构,计算并分析了各干旱状态下的干旱概率和恢复周期[9].REDDY研究了两种元启发式算法在Copula模型参数估计和干旱严重持续频率曲线推导中的应用[10].MASUD通过Copula函数建立二维分布,对加拿大Saskatchewan流域的干旱风险进行了分析[11].YUE利用混合Gumbel模型建立了相关洪峰和洪量的联合概率分布,以及相关洪峰和洪峰持续时间的联合概率分布[12].REQUENA利用二元Copula模型得到洪峰与洪量的二元联合分布,模拟了大坝溢流的回归周期,为大坝设计风险提供了参考[13].JEONG研究了气候变化对加拿大东北部21个流域春季(3 -6月)洪峰、洪量和洪峰持续时间的影响,对各洪水特征进行常规的单变量频率分析,对相互关联的洪水特征对(峰量、峰时、量时)进行基于Copula的双变量频率分析[14].JEONG将Copula模型与PMC模型相结合,提出了一种可行的间歇月流时间序列模拟方法[15].
单一的Copula函数只能描述变量间某一方面的相关性,为了全面的描述变量之间的相关性,本文构建了混合Copula函数来预测邻近水文站点的年径流量.构建混合Copula函数的关键是参数的寻优问题,为此深入研究了通用性强、模型简单,搜索速度快的布谷鸟搜索算法.布谷鸟搜索算法是YANG等通过模拟布谷鸟的产卵习性而提出的一种与莱维飞行结合的智能搜索算法[16].该算法在算法运行前期搜索速度较快,但是由于其完全依赖于随机游走机制,所以算法的局部搜索精度不高,容易陷入早熟收敛,收敛速度较慢.为了改进布谷鸟搜索算法的性能,很多学者对该算法进行了研究.为了进行混沌系统的估计和连续函数优化问题,LI等人利用正交学习策略提高了布谷鸟搜索算法的挖掘能力[17].OUAARAB等人提出了一种改进的离散CS算法来求解著名的旅行商问题[18].本文提出了自适应搜索平衡布谷鸟搜索算法(Adaptive Search Balanced Cuckoo Search,ASBCS)来进行混合Copula函数的参数寻优,并使用该混合Copula函数,以汉口水文站的年径流量为因变量,对宜昌水文站的年径流量进行了预测.
1 Copula函数
本文要研究的是两变量的水文频率分析和预测问题,主要使用的是二元Copula函数,所以这里只叙述二元Copula函数的Sklar定理.
二元Copula函数Sklar定理:令H(X,Y)为具有边缘分布F(X)和G(X)的二元联合分布函数,则存在一个Copula函数C(u,v),满足
H(X,Y)=C[F(X),G(Y)].
其中u,v均服从[0,1]上的均匀分布;H(X,Y)是具有边缘分布F(X)和G(X)的二元联合分布函数;C(u,v)对每一个变量而言,都是单调非降的,若一个变量保持不变,则C(u,v)将随另一个变量的增大(减小、不变)而增大(减小、不变).
在实际应用中,常见的二维Copula函数有三种:二维Clayton Copula函数、二维Gumbel Copula函数和二维Frank Copula函数.它们的表达式分别如式(1)、(2)和(3)所示,式中的θ是与Copula函数的Kendall秩相关系数和尾部相关性相关的一个重要参数.
(1)
(2)
(3)
在图1的(a)、(b)和(c)三个子图中,分别展示了三个函数的概率密度图,从图1中可以看出Clayton Copula函数的尾部特征不对称,其密度函数很像一个“L”,上尾低下尾高, 所以它善于敏锐地捕捉尾部不对称的数据在下尾处的变化,得到下尾处的相关性特征.Gumbel Copula函数的尾部特征也不对称,其密度函数很像一个“丁”,下尾低上尾高, 所以它善于敏锐地捕捉尾部不对称的数据在上尾处的变化,得到上尾处的相关性特征.Frank Copula函数的尾部特征是对称的,所以无法捕捉到数据尾部不对称的相关关系,反而对于对称的尾部关系很敏感.
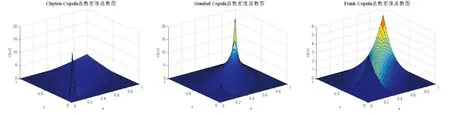
(a) Clayton (b) Gumbel (c) Frank Copula图1 三个函数的概率密度图Fig.1 Probability density graph of three functions
通过上述分析可知,三种函数分别对对称的、上尾高和下尾高的数据之间尾部相关关系比较敏感,所以它们分别有不同的应用场景.然而,现实生活中的数据都是复杂的,单一的Copula函数往往无法全面的描述数据之间的相关关系,基于此,本文将根据三个函数的特性,设计混合Copula函数,来应对现实世界中复杂多样的数据.
2 标准布谷鸟搜索算法
布谷鸟搜索算法必须满足如下3个假设:①布谷鸟每次产一枚卵,并随机将其放入一个鸟巢;②最好的巢才能被保留到下一代;③布谷鸟可以搜索的巢的数量是固定的, 宿主鸟巢主人发现外来卵的发现概率是P, 鸟蛋如果被发现,宿主将移除该蛋或直接遗弃该鸟巢.基于上述假设,布谷鸟寻找鸟巢位置的更新公式为:
xt+1,i=xt,i+α⊗levy(β),i=1,2,…,n.
(4)
其中xt,i表示经过t代更新之后第i个鸟巢的位置;⊗表示点乘;levy(β)表示Levy飞行随机游走的路线,可以用一个简单的幂律公式表示为levy(β)~μ=t-1-β;α表示步长因子,设α0是一个常数,xbest是全局最优位置,步长因子可以用式(5)来表示:
α=α0⊗(xt,i-xbest),
(5)
位置更新之后,对每一个xt+1,i,随机产生一个0到1之间的数r,与P进行比较,如果P大于r,令xi=xt+1,i,将xt+1,i丢弃,然后根据式(6)的随机游走策略求得一个新的位置对它进行替换:
xt+1,i=xi+q(xt+1,k-xt+1,j),
(6)
其中,q是0到1之间的随机数,xt+1,k和xt+1,j是位置更新之后的任意两个位置.
标准布谷鸟搜索算法的伪代码如下所示.

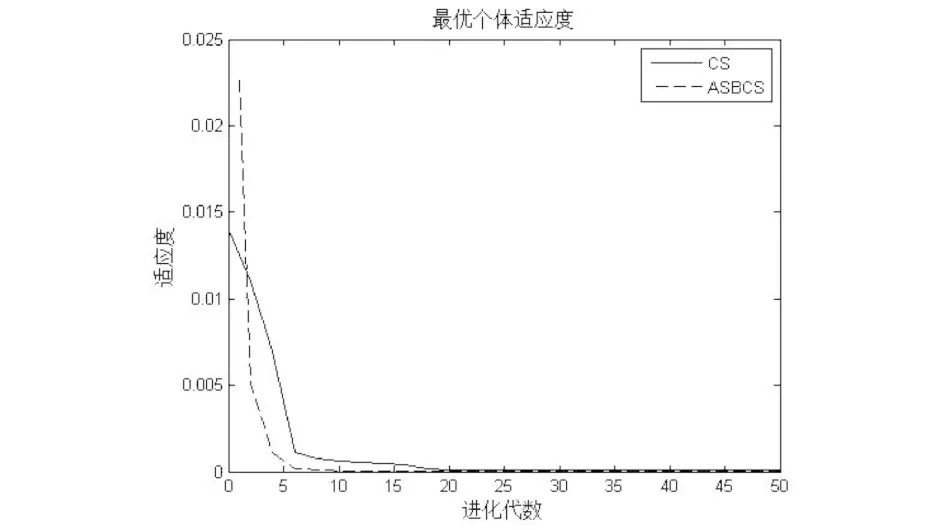
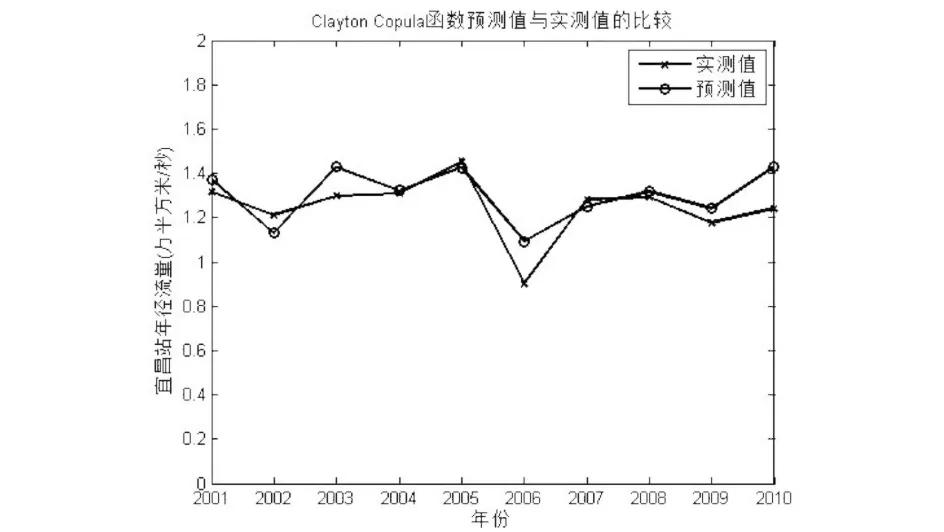
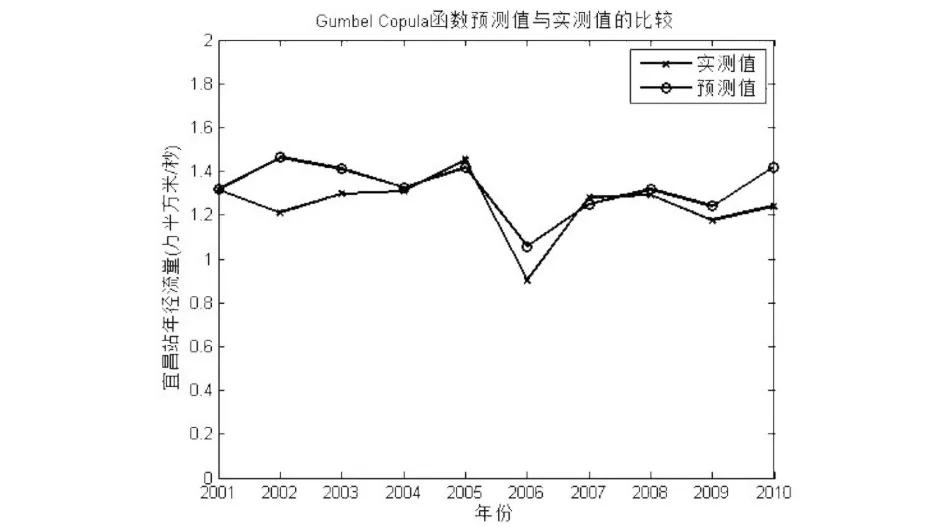
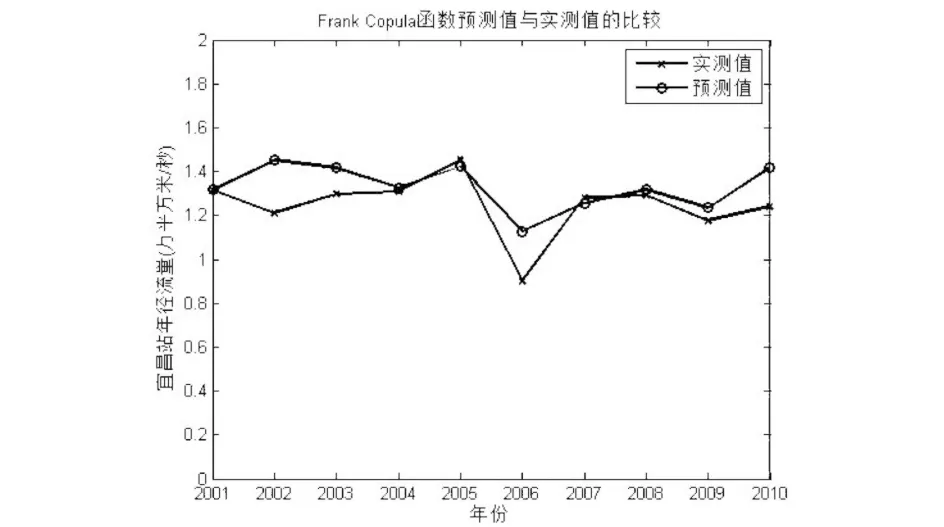
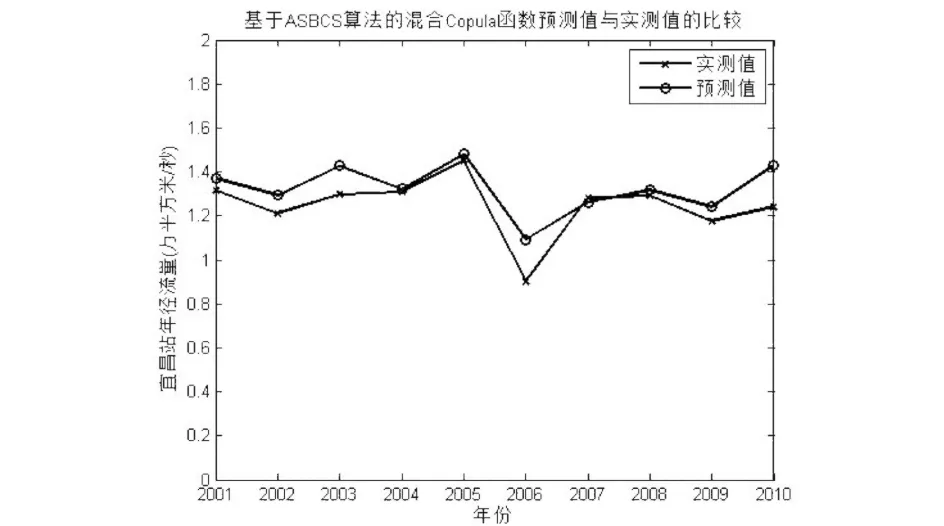
Algorithm 1 Cuckoo search algorithm via Levy flightsInput: Objective function f(x)Output: the optimal solution Randomly initialize population of n host nests xiwhile (t 标准的CS算法是一种模型简单,算法前期搜索速度较快的群智能算法,它具有如下的几个优点: (1)CS算法中的位置更新是基于Levy飞行策略的.在Levy飞行策略中,短距离的探索和偶尔较长距离的开发是相间的.这种位置更新策略能有效的扩大搜索范围,易于跳出局部最优点,增加种群的多样性; (2)相比于其他的智能算法(例如遗传算法、粒子群算法),CS算法参数少,除了种群规模,只有1个参数P,且算法的收敛速度对P不敏感,因此其操作简单,通用性更强. 同时,经过深入研究,标准的CS算法也具有如下一些缺点: (1)Levy飞行策略执行全局搜索,随机游走策略执行局部搜索,发现概率P用于调节二者之间的平衡,但是在算法执行的后期,由于个体差异的缩小,算法将比较偏重于局部搜索,从而很容易令算法陷入局部最优; (2)发现概率P和步长α都不能根据算法收敛的程度而自适应变化,因此标准算法的收敛速度慢,且个体的多样性差. 基于上述分析,本文提出了ASBCS算法,就如下几个方面对布谷鸟搜索算法进行了改进. (1)对步长因子进行了改进,令步长因子随着算法的迭代次数自适应的变化. 标准布谷鸟搜索算法的步长公式如式(5)所示, 其中α0是一个常数,步长因子只能随着位置的更新而发生不规律的变化,不能随着算法迭代次数的增加而自适应调整,因此,本文在步长公式里增加了迭代次数因子,具体如式(7)所示,其中α0max和α0min是根据实际情况给出的步长的最大值和最小值,T是总的迭代次数,t是本次的迭代次数. (7) (2)在算法后期,对全局搜索和局部搜索进行了平衡. 在标准布谷鸟搜索算法的迭代后期,因为个体之间的差距变小,造成搜索偏向于局部搜索,容易令算法陷入局部最优,为了改善标准布谷鸟搜索算法的这一缺点,对公式(7)进行了改进,改进之后的步长公式如式(8)所示. (8) 相对于CS算法,ASBCS算法在两个方面进行了改进,提高了算法的性能,主要表现在如下几个方面. 首先,步长因子的调整,令算法中解的跳跃,不止依赖于当前解和全局最优解,还与迭代次数成反比,随着迭代次数的增加,令算法更加趋向于局部搜索,对局部的解区间进行深度挖掘,提高了算法的收敛速度. 其次,在提高收敛速度的同时,为了提高解的多样性,避免算法陷入局部最优,在算法迭代的后期采用了全局搜索和局部搜索的平衡策略,以一定的概率P1来平衡两种搜索方式,一方面加快了收敛速度,另一方面又令算法不断的跳出局部最优,增加解的多样性,令算法在全局和局部搜索之间灵活的转换,从而达到两种搜索的平衡. 为了比较标准CS算法和本文所提出的ASBCS算法的性能,分别采用两种算法对一个经典函数进行寻优,该函数如式(9)所示,它在(0,0)处取最小值. (9) 用两种算法对该函数进行寻优的实验结果如图2所示.从图中可以看出,ASBCS算法比CS算法具有更快的收敛速度和更好的精确度. 图2 标准CS算法和ASBCS算法性能比较Fig.2 Comparison of performance between standard CS algorithm and ASBCS algorithm 通过深入分析二维Clayton Copula函数、二维Gumbel Copula函数和二维Frank Copula函数的概率密度图,发现这三种函数分别适合的是下尾相关、上尾相关和尾部对象的两变量相关关系,利用它们各自的优势,可以将它们融合在一起,设计成混合Copula函数,从而令Copula函数适合描述各种复杂的两变量关系.混合之后Copula函数可以描述为式(10): C=ω1CFrank(u,v,α)+ω2CGumbel(u,v,β)+ ω3CClayton(u,v,γ), (10) 将式(1)、(2)和(3)式代入,可以得到具体的混合Copula函数表达式如式(11)所示. (11) 式中α、β、γ、ω1、ω2、ω3由改进的布谷鸟搜索算法寻优得到. 寻优时改进的布谷鸟搜索算法的适应度函数为式(12)所示: (12) 本文以汉口站的年径流量作为自变量,宜昌站的年径流数据作为因变量,以它们1952-2000年的数据作为历史数据进行训练,以汉口站2001-2010年的数据作为自变量,来预测宜昌站2001-2010年的年径流量.分别采用Clayton Copula函数、Gumbel Copula函数、Frank Copula函数以及本文所提出的混合Copula函数进行预测,实测值与预测值的比较如图3、图4、图5和图6所示. 图3 Clayton Copula函数求取的宜昌站年径流预测值与实测值对比Fig.3 Comparison between the predicted annual runoff calculated by Clayton Copula function and the measured annual runoffin Yichang station 图4 Gumbel Copula函数求取的宜昌站年径流预测值与实测值对比Fig.4 Comparison between the predicted annual runoff calculated by Gumbel Copula function and the measured annual runoffin Yichang station 从图3、图4和图5中可以看出单一的Copula函数在某些年份预测的精度非常高,实测值与预测值基本重合,但是在另一些年份预测精度又很低,极大一部分原因是由于气候、人为引流或者建造工程等因素造成的,但是也有一部分原因是由于Copula函数的性能造成. 图5 Frank Copula函数求取的宜昌站年径流预测值与实测值对比Fig.5 Comparison between the predicted annual runoff calculated by Frank Copula function and the measured annual runoffin Yichang station 比较图6和图3、图4、图5可以发现,相比Clayton、Gumbel和Frank三个单一的Copula函数,基于ASBCS算法的混合Copula函数具有更高的预测精度. 为了更好地比较四个Copula函数,将四个Copula函数预测宜昌站2001-2010年的年径流量的相对误差全部列于表1中,从表1可以看出,混合Copula函数可以弥补三个单一Copula函数的缺陷,比如在2001年Clayton的预测精度远远低于Gumbel和Frank函数,但是在2002年Gumbel和Frank函数的相对误差又远远高于Clayton函数,而混合Copula函数因为将三个函数结合起来,取其优点,所以很好的融合了三种函数,在2001年和2002都取得了更好的预测效果.比较四个预测方法的平均相对误差,发现基于ASBCS算法的混合Copula函数具有更好的预测精度. 图6 基于ASBCS算法的混合Copula函数求取的宜昌站年径流预测值与实测值对比Fig.6 Comparison between the predicted annual runoff calculated by hybrid Copula function based on ASBCS algorithm and themeasured annual runoff in Yichang station 表1 四个函数预测宜昌站2001-2010年的年径流量的相对误差比较Tab.1 The relative error comparison of the annual runoff in Yichang station from 2001 to 2010 predicted by four functions 本文提出了基于自适应搜索平衡的布谷鸟搜索算法,对混合Copula函数进行参数寻优,以汉口水文站和宜昌水文站的历史数据作为训练集,以10年间的汉口水文站的年径流量为自变量,对宜昌水文站10年间的年径流量进行了预测.本文所构建的混合Copula函数是在深入研究了三种二元Copula函数,详细分析了三种函数的参数设置以及适合应对的变量关系之后所构建的.实验结果证明了ASBCS算法收敛速度快,寻优精度高,用于混合Copula函数寻优之后,对宜昌水文站10年间的年径流量的预测精度明显高于三个单一的Copula函数.本文所提出ASBCS算法对其他应用中的参数寻优具有重要的参考意义,该邻近水文站的年径流量预测方法可以推广至任何两个地域上较邻近水文站的年径流预测.在今后的研究中,将进一步混合Copula函数,研究更优的群智能算法来进行混合Copula函数的参数寻优.3 ASBCS算法
3.1 标准CS算法性能分析
1.2 ASBCS算法
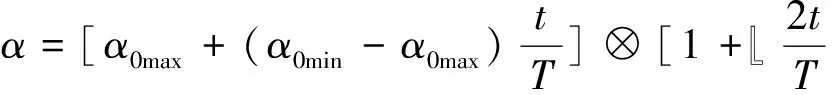
3.3 ASBCS算法的性能分析
3.4 ASBCS算法与CS算法的性能比较
4 基于ASBCS算法的混合Copula函数
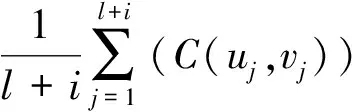
5 实验数据与分析

6 结语

