基于排队论的舰载机起降过程模型

顾实

舰载机起降过程是连接航母与舰载机的重要一环,该环节的优化将提高舰载机的起降效能,因此,找到影响舰载机起降的关键因素,进而优化其起降过程具有重大现实意义[1].近年来国内有关舰载机起降的研究逐渐开展,并取得了一定的成果.岳奎志通过分析动力学理论,建立了舰载机动态调运模型[2];赵远征分析了航母关键系统对架次率的影响[3];杨炳恒等进行了对舰载机甲板作业流程的优化研究[4];崔博等根据改进的自适应遗传算法进行了保障人员配置仿真系统[5];陈成等建立了舰载机出动回收仿真模型[6].由于舰载机起降过程是复杂离散事件系统,本文将采用排队论模型进行仿真分析、找到影响舰载机起降效能的关键环节,为后续提高舰载机起降效能打下基础.

1 舰载机起降过程分析

舰载机起降过程包括众多连续环节.通常大部分舰载机停在机库,当作战任务下达时,首先将机库中舰载机通过升降机提升至甲板技术站位,或将临时停机位的舰载机牵引至甲板技术站位.舰载机经过一系列保障活动后才能起飞.在某架飞机起飞准备过程中,飞行甲板的其他场所也在为已经着舰的舰载机进行检查、加油和退弹或挂弹作业.一般而言,舰载机起飞出动过程的顺序为:升降→牵引、系留→飞行前检查→电燃气液保障→挂弹→起飞.舰载机再次起飞出动过程的顺序为: 牵引、系留→退弹→排除故障→飞行前检查→电燃气液保障→挂弹→起飞[7].

由于舰载机数量庞大且甲板面积有限,因此舰载机着舰后,必须将其及时移动到合适的位置,并进行飞行后的保障工作,如卸载弹药、飞行后检查、排除故障和保养工作,若无后续任务,则下降至机库进行保养.对于驻留保养的舰载机来说,飞行后检查也是十分重要的环节,及时检测出存在故障的舰载机并维护整修[8-9].

舰载机飞行后活动过程的顺序可总结为:

牵引→退弹→飞行后检查→升降→排除故障→附加设备→保养.

综上,一次完整的舰载机起降流程如图1所示.

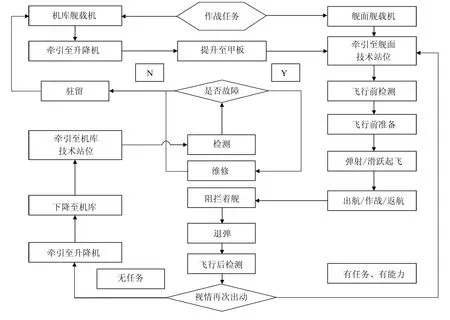
图1 舰载机起降流程图

舰载机着舰过程依然存在很大的风险,一旦舰载机没钩住阻拦索,舰载机必须立即在有限的区域加速到安全起飞的离舰速度,并在空中盘旋等待下一次着舰的机会.这一过程被称为“逃逸复飞”[10],目的是为了提高舰载机安全着舰的概率.

2 舰载机甲板保障活动分析

为了方便描述,首先引入几个概念: 技术站位、临时停机位.技术站位是指舰载机接受各项保障服务时的站位.由于舰载机较大且甲板空间有限,一般将舰载机系留固定在技术站位,通过保障人员移动服务设备来进行服务,而不是舰载机不断转场到各个服务的技术站位.临时停机位是指已完成全部保障活动、只等待起飞的舰载机临时停靠的机位,不影响其他舰载机接受服务.

在机库中的舰载机首先通过升降机升至甲板,并牵引到服务机位,由保障人员将舰载机进行系留固定.固定后,保障人员需要对舰载机进行飞行前检测[11-12].在确定舰载机的状态性能达标后,机务人员将对舰载机进行相应的电燃气液的补充工作,包括充气服务、换胎服务、充电服务及加油服务[13].通常舰载机停在服务机位,由保障人员牵引油管在服务机位为舰载机进行加油服务.有时加油服务会不得已停止,这是因为其他舰载机的转场作业可能会压坏油管,这时需要将油管暂时移除,等待其他舰载机转场作业结束后再继续加油.

除了以上提到的确保舰载机安全飞行的保障工作外,为了完成作战任务,舰载机还需要装备相应的武器弹药.当舰载机达到挂弹服务机位后,由保障人员组成的挂弹小组负责将弹药运送到挂弹服务机位.在挂载弹药之前,舰载机需要先关闭引擎,并将舰载机上的引信(cad)移除.之后挂弹小组将武器弹药装载至舰载机的相应位置,并将引信重新安装.在安装好之后,为了确保安全还需要进行武器安全检查.以上是一架舰载机起飞前完整的保障过程.将上述甲板保障过程用程序框图如图2所示.

武器安全检查完毕后就进入准备起飞步骤,如果有舰载机正在起飞就让其先到临时停机位排队等待,如果临时停机位排队的舰载机达到上限,武器安全检查的舰载机就在原地驻留,等待临时停机位有空位或者可以直接起飞就可以起飞,其中先进入排队先起飞.武器安全检测到准备起飞,如果空中有舰载机准备降落或者空中有舰载机驻留,那么舰载机降落优先.舰载机降落时,根据舰载机是否故障或油料耗尽,为不同舰载机赋予不同的降落优先级,降落顺序为:油料耗尽＞故障＞空中驻留.另外,降落时也会存在复飞的可能性.

飞行检测完成后,如果舰载机有任务并且无故障,看舰载机能否牵引至技术站位,这取决于升降机是否还有舰载机在排队,以及技术站位所容纳的舰载机是否达到上限,升降机有排队或者技术站位容纳的舰载机达到上限,那么飞行检测完成后就下降到机库再排队,如果舰载机有故障或者任务已完成,那么就牵引至机库不再出动.

在舰载机起降过程中,恶劣海况环境将会对甲板保障任务产生影响,在某个时间段内舰载机会不能起飞,或者所有服务全部停止,只有等待气象影响结束后,才能正常运作[14].这也是在仿真建模时需要考虑的问题.

3 基于排队论的舰载机起降过程建模

通过前文的分析,可看出舰载机起降过程是典型的离散事件系统.这种系统存在较大的随机因素,变化关系较为复杂,很难找到一般数学方程类模型对该系统进行定量描述,而采用流程图或网络图的形式则能更好地描述该系统,在图2流程图的基础上,确定出各环节相关的时间参数,就得到描述舰载机甲板保障作业的离散事件系统模型.排队论模型就是用于建立离散事件系统模型的主要方法.舰载机在航母甲板上接受起飞前和降落后的各项保障工作,就是一个排队系统: 舰载机相当于顾客,保障人员与各种资源结合构成服务机构.由于舰载机到达及服务时间存在随机性,以及甲板资源有限,当作战任务需要较多数量舰载机时,就会产生排队现象.为了解决排队现象,排队论应运而生.

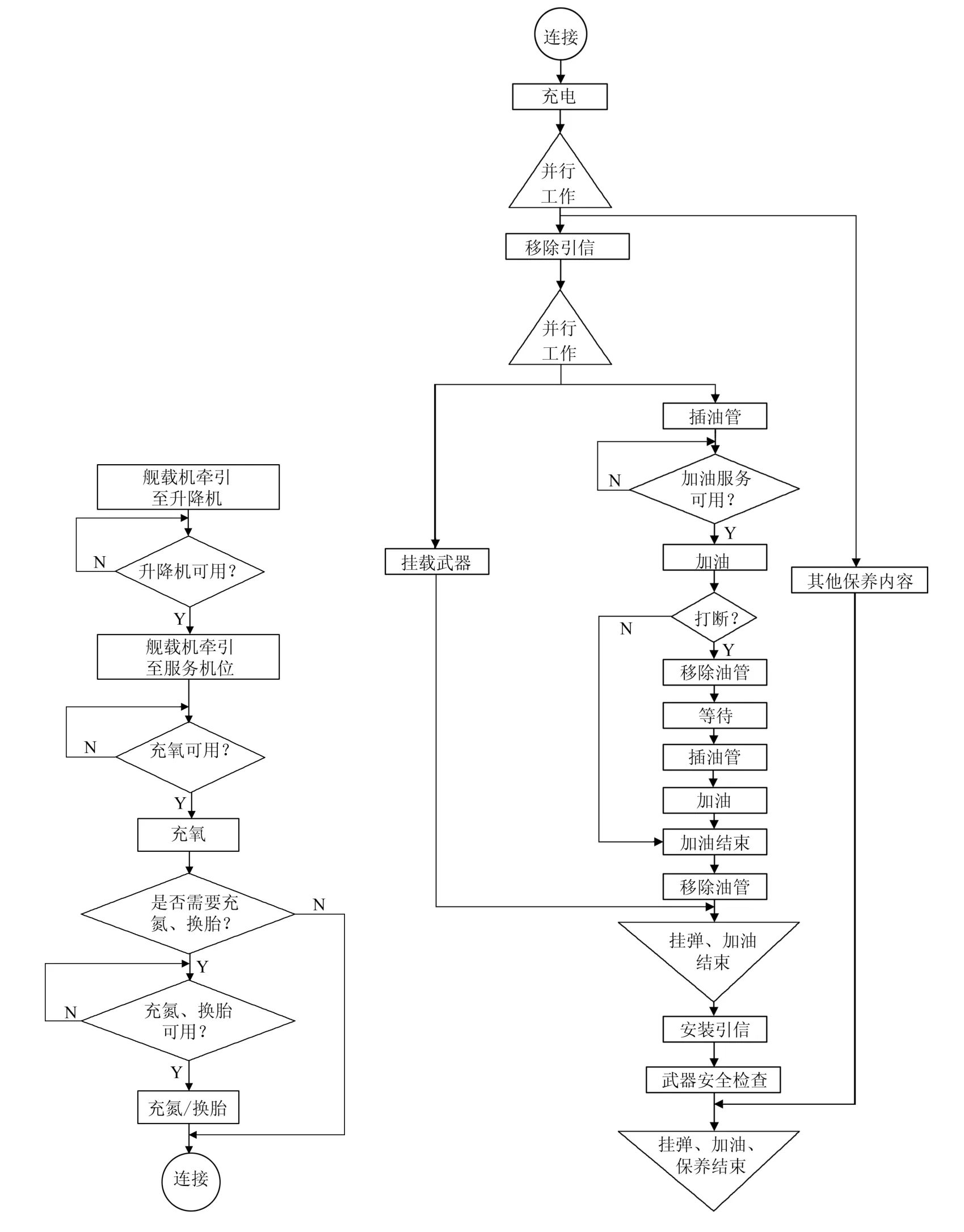
图2 舰载机甲板保障作业流程图

排队论主要应用于解决随机因素导致的排队现象.排队现象反映了顾客与服务机构之间的服务关系,两者共同构成了一个排队系统.一般的排队系统如图3所示.顾客作为输入流随机到达服务机构,并根据服务机构的状态,按照一定规则排队等待接受服务.接受服务后,顾客作为输出流离开服务机构.排队规则和服务规则将决定队列中的顾客接受服务的顺序.

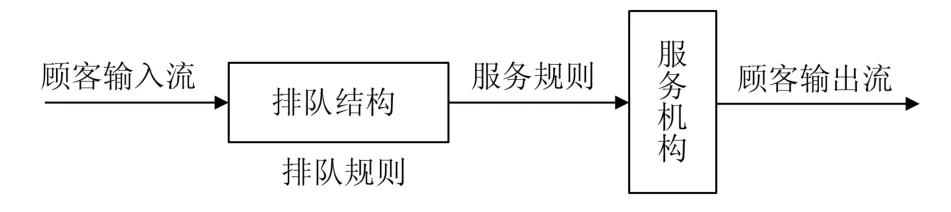
图3 排队系统

在作战任务的驱动下,以及有限的甲板面积和有限的航空保障资源(保障人员和设备资源)的约束条件下,舰载机甲板保障活动存在大量的随机因素,如舰载机到达时间和各环节的保障时间都具有随机性.因此,甲板保障活动的这种不确定性可以运用排队论来研究.若把舰载机甲板保障活动看作是一个排队系统,则舰载机相当于顾客,保障人员与保障设备看作是该排队系统的服务机构,称作服务台,如加油服务台、挂弹服务台等.结合前文介绍的排队论的相关知识,分析舰载机甲板保障排队系统如下.

在排队系统中包含3 个基本组成部分,即输入过程、排队规则和服务机构,对此进行分析,需要确定每种顾客到达模式、保障活动的服务台数量、排队数、排队规则、服务规则、完成一种保障活动需要的时间分布等[15-16].这样得到排队论模型后便可运用模拟仿真的方法进行仿真,计算出舰载机航空保障中甲板活动的保障效率.

3.1 输入过程

舰载机出动的顺序作为排队系统的输入流,且需要的舰载机数量是有限的.舰载机一般停留在空间有限的机库,舰载机从机库单独到达升降机,且舰载机相互之间的到达时间是随机的,并将其简化为负指数分布过程,即舰载机到达时间符合负指数分布.

3.2 排队规则

由于各个保障环节的保障时间不同,当舰载机到达服务站位时,服务台可能正在为其他舰载机服务.这时就产生了排队现象,舰载机需要按照排队规则排队等待,符合等待制的排队规则.一般情况下,在排队队列中的舰载机为单队排列,且按照到达服务站位的先后顺序接受服务,优先到达服务站位的舰载机会优先接受服务,即为先到先服务.

当然舰载机起飞和降落环节有所不同,需要特殊说明: 为了最大程度地保证舰载机的安全,舰载机的起飞和降落不能同时进行.如果有空中有舰载机准备降落或者空中有舰载机驻留,那么应当优先舰载机降落,而待起飞舰载机需等待着舰机着舰完成后再起飞.

3.3 服务机构

舰载机起降过程所需要的各个保障环节中涉及的服务人员和服务设备即为该排队系统的服务台,如升降、加气、加油、加电、挂弹等等环节,不同服务台的数量有所不同,一般为多个.单队多服务台类型的意思是在某一环节中,服务台与服务台之间组成并联关系;在整个排队系统中,如果环节与环节之间组成串联关系就称为多个单队多服务台模型串联模型.

服务时间是指舰载机接受各种保障活动的时间.舰载机接受保障服务的时间是随机的,通常用概率分布来描述其时间规律,且各个舰载机接受服务的时间是相互独立的.根据实际情况,舰载机接受服务台的服务时间服从均值为1/µi的负指数分布,其中µi为某一服务器的服务率,表示单位时间内可以服务的舰载机数.以加油服务为例,若加油服务台的服务率µi= 3.6,则表示加油服务台每小时可服务3.6架舰载机,也就是每架舰载机的加油时间为1 000/s(16.7 min).其他服务台类似.由于在一段时间内舰载机到达数量是有限的,因此认为该过程是稳定的.

所以,综上所述,建立的舰载机起降甲板保障活动模型按分类属于M/M/C 排队系统模型,且为多个单队多服务台串联模型.以舰载机接受升降机服务为例,舰载机通过升降机由机库升至甲板的过程即为典型的M/M/1 排队系统模型.

舰载机到达升降机的时间服从参数为λ 的负指数分布,升降机的服务时间服从参数为µ 的负指数分布.M/M/1 排队模型的各类参数求解如下:

1) 系统中等待升降机服务的平均舰载机数Ls(正在接受升降的舰载机与等待升降的舰载机总和):

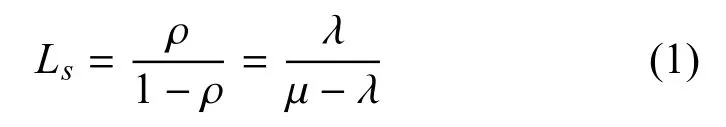
2) 由Little 公式得舰载机在系统内的平均滞留时间Ws:

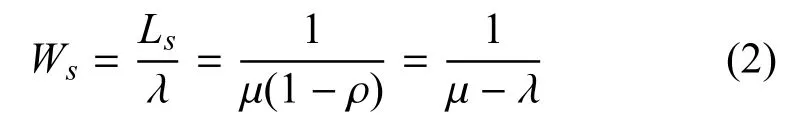
3) 系统中等待升降机服务的平均舰载机数Lq=Ls-Lf,Lf为正在接受升降机服务的平均舰载机数,其取值为0 或1,对应的概率分别为1-ρ 和ρ,则Lf=0×(1-ρ)+1×ρ,由此得到:

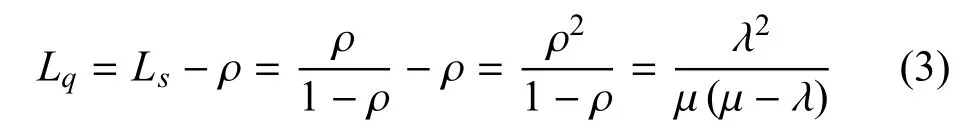
4) 由Little 公式得舰载机在系统内的平均排队时间Wq:

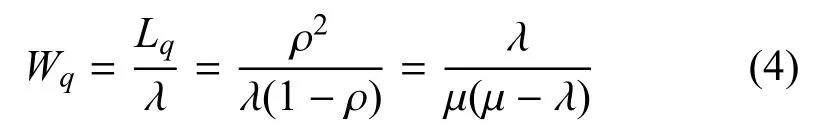
舰载机后续其他保障活动服务台的事件到达时间,需要根据前一项保障活动的结束时间而定,因此难以建立类似的定量模型,只能在确定其排队规则和服务机构的参数后,仿真计算.

4 仿真实现

4.1 案例想定与参数设置

1) 情况想定: 计划训练时间为8 时～18 时,计划起降总架次为40 架.其搭载舰载机组成为J-001型舰载机和J-002 型舰载机各10 架.装载的武器为A、B、C、D 4 种类型武器.

2)训练环境:9 时～11 时的气象名称qx-1.该气象会导致舰载机存在30%的几率不能一次阻拦着舰成功,即需要复飞.

3)资源数量及服务台参数设定

通常海上训练任务在开始之前需要制定训练计划,包括起降计划参数、训练时间与环境参数、舰载机数量与类型、服务台数量与类型等.表1为各服务平台参数信息与缺省时间[17].

4.2 仿真实现与结果分析

由于仿真中存在概率事件,因此一组仿真实际是连续仿真10 次,得到的结果即所获得的平均值.获得定量指标数据值如图4所示.

为了找到影响舰载机起降效能的关键环节,对每个服务台的数据进行分析,并以条形图的形式给出,对比不同服务台之间的服务时间、排队时间和滞留时间.如图5所示,黄色代表服务时间,蓝色代表排队时间,红色代表滞留时间.

从仿真结果来看,在舰载机起降过程中挂载武器服务台位的排队时间较长、加油服务台位的滞留时间较长,是影响舰载机起降环节的关键因素.舰载机挂载武器的服务时间过长,而加油服务可以与挂载武器服务并行开展,在加油服务结束后,武器还没有挂载完毕,从而导致了加油服务台滞留时间过长,这些都是影响舰载机起降过程的重要因素,增加挂载武器或加油服务台位对舰载机起降流程时间的影响方式需要经过多次仿真.在后续工作中可以采用控制变量法,在本次仿真(即初始状态)基础上,每次改变一种服务台的数量,根据获得的数据指标变化情况,来找到最佳的服务台位设置方式,从而提高舰载机起降效能.

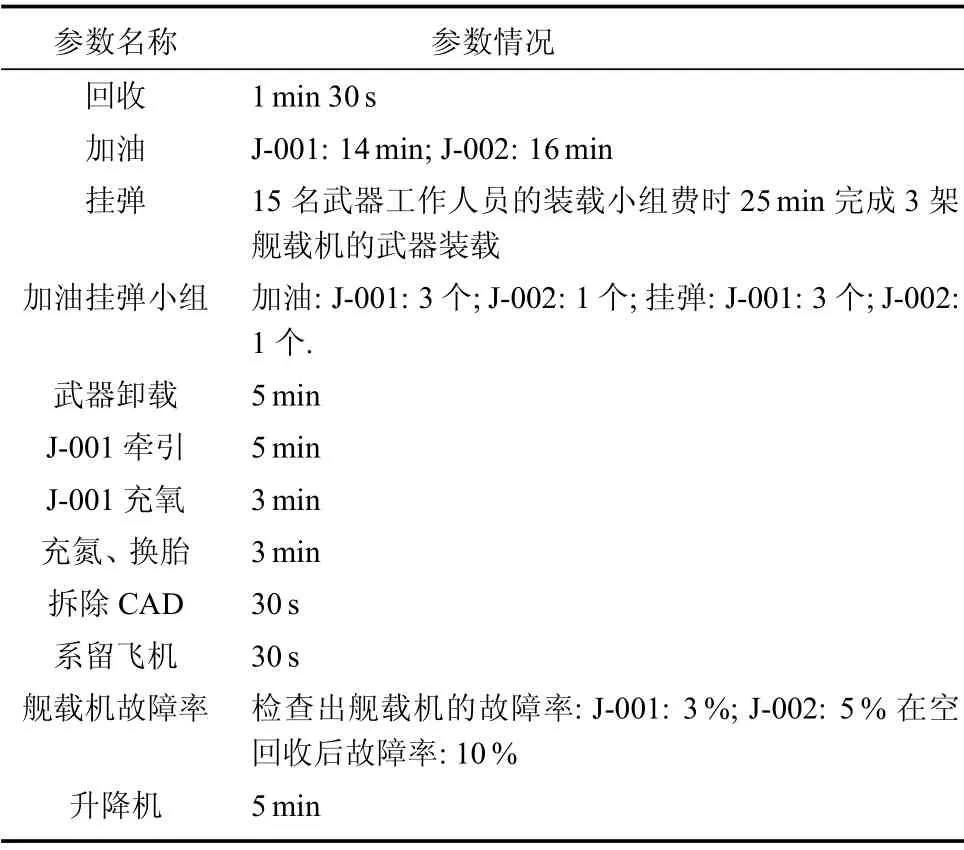
表1 甲板保障时间实例

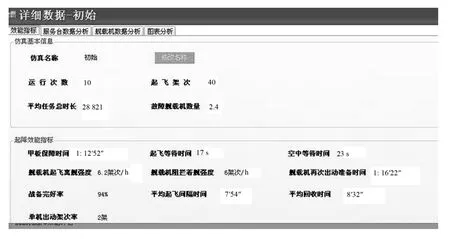
图4 初始仿真数据

5 结论

本文指出了舰载机完成起降过程中的辅助设施与甲板面积的局限,反映了该过程的复杂性与危险性;根据航空机务工作规定,明确了舰载机整个起降过程的基本流程,以程序框图的方式给出,并在对舰载机起降涉及到的具体环节进行详细描述的基础上,建立了基于排队论的舰载机起降过程模型,最后进行了仿真分析.从仿真结果来看排队论模型对分析舰载机起降过程具有较好的效果,能够直观分析出各个保障环节服务时间、排队时间和滞留时间,对于排队时间和滞留时间较长的保障环节可以尝试增加服务台位等措施,其可行性有待后续工作论证.

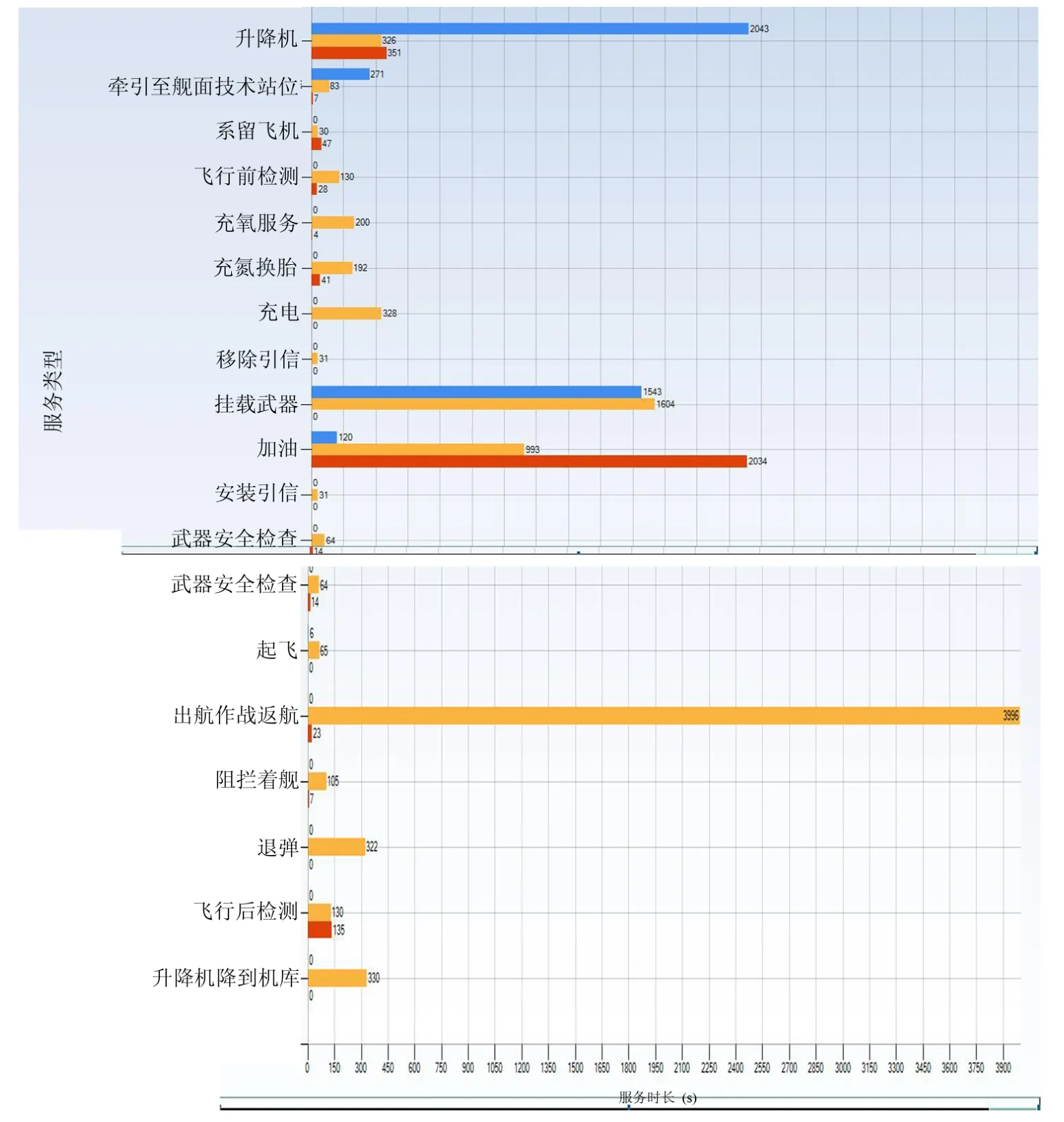
图5 服务台数据分析