基于渐进法的船舶横摇非线性阻尼系数识别

孙金伟，邵 萌，邵珠晓，李选群，万晓正，赵环宇，刘海丰

（1.中国海洋大学工程学院，青岛266100；2.山东省海洋工程重点实验室，青岛266100；3.齐鲁工业大学（山东省科学院）海洋仪器仪表研究所，青岛266001；4.山东省海洋环境监测技术重点实验室，青岛266001）

0 引 言

船舶横摇阻尼的准确估算是正确预报波浪中横摇运动的前提。小角度横摇时，船舶横摇运动可以用线性方程描述，但当横摇幅值增大时，必须考虑非线性效应。横摇非线性主要表现在回复力矩的非线性和阻尼的非线性，很多学者对非线性的阻尼和回复力矩数学模型开展了研究[1-4]。

船舶横摇回复力矩可由不同阶次的奇次多项式函数表示，回复力矩系数可通过与流体静力学计算得到GZ曲线进行拟合获得[5]。而对于横摇阻尼项，目前尚未有完备的理论计算方法，现有的船舶耐波性评估的势流理论不能预报横摇运动中由于摩擦、旋涡和流动分离等因素产生的粘性阻尼[6]。基于模型试验获得的经验公式在实际使用中较为方便，但是仅对特定船型适用[7-9]。因此在工程实践中常用模型试验的方法来确定船舶横摇阻尼系数。

最早利用模型试验进行横摇阻尼系数估算的学者是Froude（1872）[10]。Wassermann（2016）等[11]对不同的模型试验技术，包括衰减横摇试验和强迫横摇试验方法等进行了研究总结。Spouge（1988）[12]对于不同学者提出的各类不同阻尼系数识别方法和结果进行了总结比较，并探讨了各种方法的识别精度。Mathisen 和Price（1985）[13]提出了估算衰减横摇和强迫横摇试验阻尼系数的方法，研究发现线性加平方项阻尼模型比线性加立方项阻尼模型具有更好的优越性。Roberts（1985）[5]提出了根据自由横摇衰减曲线估算非线性横摇阻尼项的计算方法，该方法适用于小阻尼情形，不限制回复刚度的非线性程度，但遗憾的是作者给出的例子中并没有考虑强非线性的回复力矩。Chan 等（1995）[14]将徐兆（1985）[15]提出的一种新的渐进法应用于船舶非线性横摇阻尼系数估算中，该方法适用于大角度横摇以及强非线性回复力矩，但是其在不同初始横摇角度下的阻尼系数识别结果存在一定计算误差，识别精度仍有待提高。李红霞等（2005）[16]根据衡量耗散的观点利用横摇试验衰减曲线，提出了一种非线性阻尼识别方法，通过算例分析认为二次阻尼模型和三次阻尼模型对船舶横摇的作用是等效的。马新谋等（2013）[17]采用李红霞等提出的能量法，依据两栖车辆自由横摇衰减曲线确定了两栖车辆的非线性阻尼项。马山等（2012）[6]基于模型试验的横摇衰减测量数据，采用能量法进行了船舶横摇阻尼系数的研究，并通过实验证实了采用能量法获取的横摇阻尼系数结合势流兴波阻尼预报横摇运动具有较高的精度。

本文基于非线性力学中的渐进法，发展了一种基于横摇自由衰减数据的阻尼系数识别方法，通过数值仿真和对比研究分析，验证了该方法的高精度和适用性，最后将该方法应用到船舶横摇衰减实测数据，识别其非线性阻尼系数，数值模拟结果与试验数据表现出了较好的一致性。

1 渐进法介绍

对强非线性系统，其运动可由下列微分方程描述

式中：ε为小参数，函数g( x )和f(x,x)满足如下关系：

根据摄动理论[18]，（1）式具有如下形式的广义渐进解

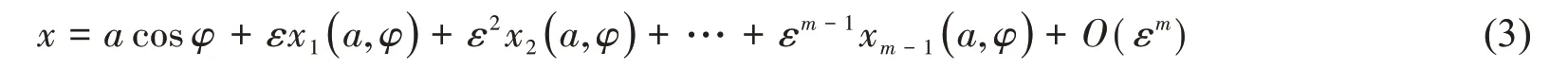
式中：a 是振幅，φ 是相位角，均为时间的缓变函数，x1,x2,…,xm-1是相位角φ 的周期函数，其周期为2π。a和φ由如下微分方程决定：

为简化计算，（1）式的解通常由其一阶近似解表示[15]

式中：

因此要求解（6）式，则需要求解（7）式中参数A1( a )，Φ0( a,φ )和Φ1( a,φ )。具体步骤如下：

令ε = 0，则由（7）式可知：a= 0，Φ0( a,φ )= φ。当ε = 0时，（1）式变为

（8）式两边同乘以x并积分可得

式中，C是积分常数，且有

假定初始条件为x(0)= a,x( 0 )= 0，则由（9）式可确定C = V(a)。将（6）式代入（9）式中可得

由（6）-（7）式可得

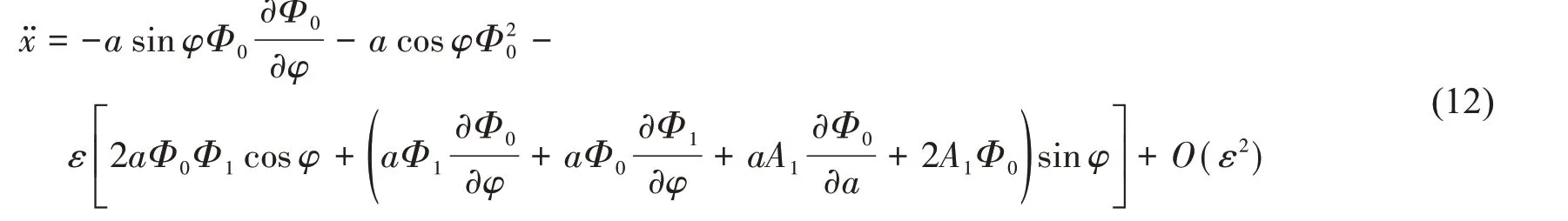
把函数g( x )展开成ε的幂级数

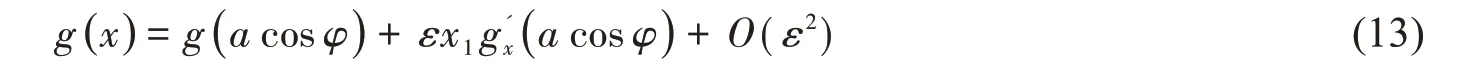
将（12）和（13）式代入（1）式，使等式两边ε 项的系数相等，得到

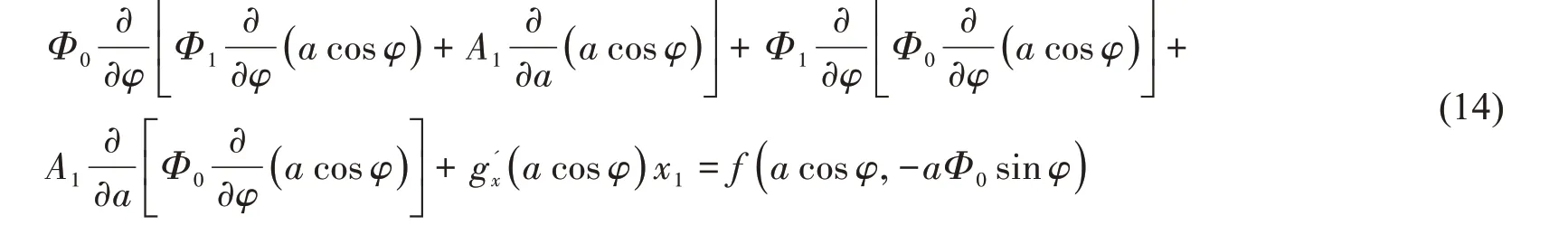
令φ = 2π，可以求出A1表达式

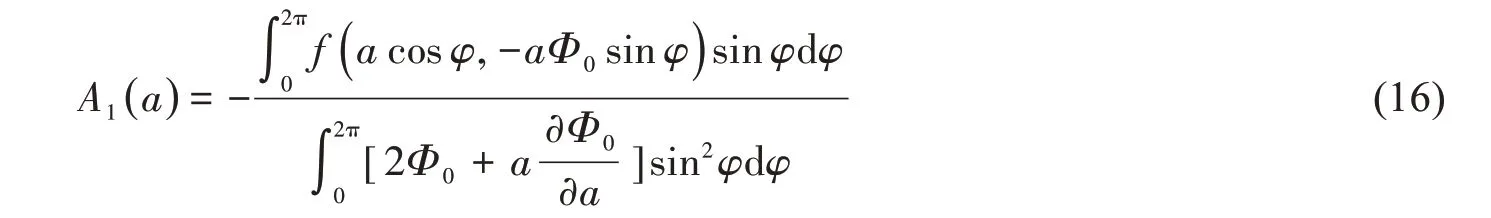
令φ = π，可以求出Φ1表达式。至此，（7）式中的未知项A1( a )，Φ0( a,φ )和Φ1( a,φ )全部求出，于是方程一阶近似解的表达式（6）可求出。

2 阻尼系数识别

船舶横摇非线性阻尼选用如（17）式所示的线性加平方阻尼模型，回复力矩用如（18）式所示的奇次多项式函数表示：

（18）式中的幂次数项j和回复力系数kj可由流体静力学计算的GZ 曲线进行拟合求得。将（17）式和（18）式代入（1）式，得到船舶横摇非线性运动方程如下

由（10）式和（18）式可得

将（17）式代入（16）式，可得

式中，

P( a )和Q( a )是幅值a的函数，可以用多项式函数( a )和( a )近似表示：

式中，系数p11，p12，q11和q12可通过最小二乘法进行数据拟合得到。于是（21）式可写为

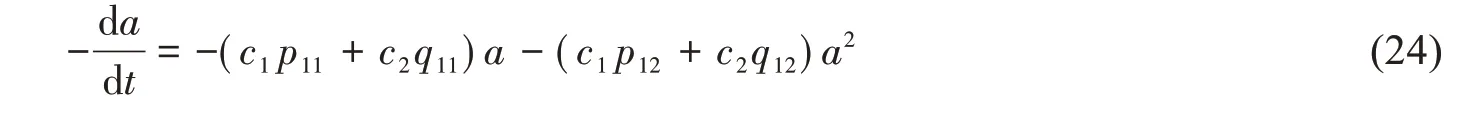
横摇固有周期T0等于衰减数据的平均周期[13]，可由（26）式确定

式中，x0是初始横摇角。根据横摇衰减数据，采用间隔半个周期的横摇角幅值差与相邻两次的平均横摇角幅值绘制横摇消灭曲线，对数据进行拟合可得到曲线近似表达式为

由（25）和（27）式可求得阻尼系数c1和c2的估算值：

（28）式中阻尼系数的识别精度与初始横摇角有关。为提高阻尼系数识别精度，本文进行如下的迭代误差修正：将（28）式中的阻尼系数初次估算值和代入船舶横摇运动方程（19）式中，初始条件不变，仍为x( 0 )= x0和x(0)= 0，采用龙格库塔方法进行数值求解，可仿真生成自由横摇衰减曲线，求得新的横摇消灭曲线

同理，再次根据（28）式，可以求得阻尼系数的第二次估算值：

前两次阻尼系数估算值的相对误差为：

3 有效性验证

为验证本文提出的阻尼系数识别方法的有效性，选用（33）式的横摇动力学非线性方程作为算例[14]，初始条件x( 0 )=0.3 rad( 0 )= 0。通过数值方法模拟生成自由横摇衰减曲线，然后用本文方法识别其阻尼系数，并与精确值相比较以验证方法的有效性。横摇运动响应采用四阶龙格库塔法求解，时间间隔为0.01s，计算时长为50s。图1 和图2 是模拟得到的横摇衰减曲线及相应的消灭曲线。回复力矩表达式为g( x )= 2.25x - x3，具有强非线性特征，其最大回复力矩对应的横摇角为0.866 rad，回复力矩曲线如图3所示。

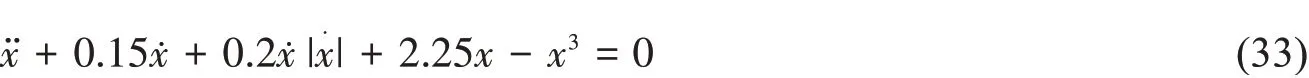
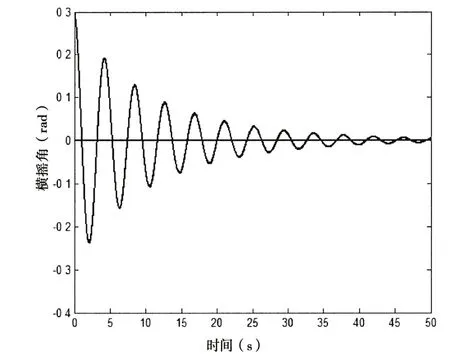
图1 模拟自由衰减曲线 Fig.1 Simulated free-decay curve

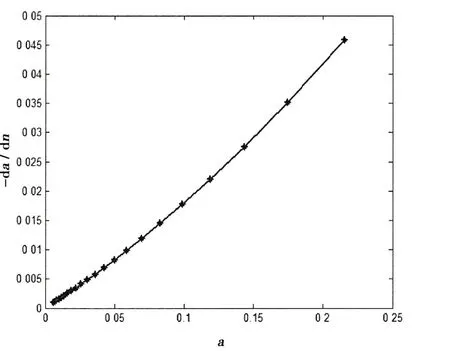
图2 横摇消灭曲线Fig.2 Roll extinction curve

根据消灭曲线数据拟合结果，（27）式可写为

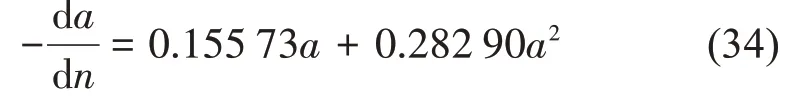
根据（20）式和（11）式计算可得

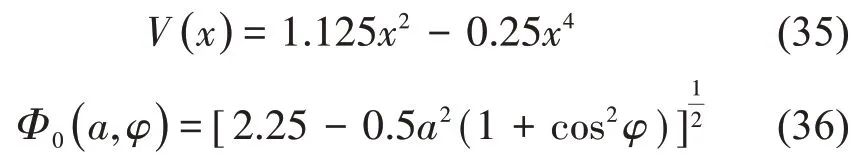
根据（23）式可得

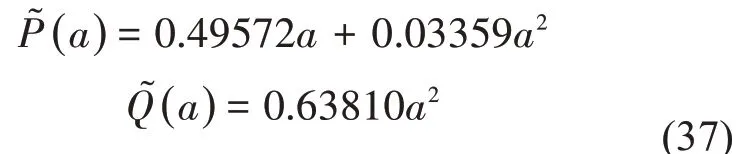
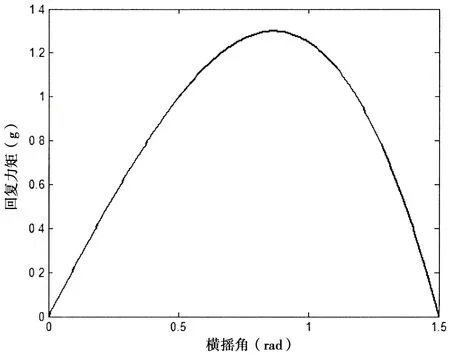
图3 非线性回复力矩Fig.3 Nonlinear restoring moment

由（26）式可得横摇衰减运动固有周期T0=4.253 16 s，根据（28）式计算可得到阻尼系数的第一次估算值为= 0.147 83 和= 0.200 70；将和作为新的阻尼系数代入到（33）式中，重复上述计算过程，得到阻尼系数第二次估算值=0.14567和=0.20144，前两次阻尼系数估算值之间的相对误差为η1=-1.458 74%和η2=0.367 16%；阻尼系数的第三次估算值=0.143 53和= 0.202 21，后两次阻尼系数估算值之间的相对误差为=-1.469 20%和= 0.383 33%。于是，根据（32）式可求得一阶和二阶阻尼系数的最终估算值c1 =0.150 00和c2= 0.200 00，与（33）式中阻尼系数准确值相等，识别误差为零。

为考察本文方法的精度，开展不同横摇角幅值下的参数研究，将船舶横摇方程的阻尼系数识别结果与采用其他方法得到的估算结果进行对比分析。

采用本文方法对（33）式在不同初始横摇角时的非线性阻尼系数进行了识别，计算结果见表1，同时将本文中阻尼系数的识别结果和相对误差等与文献[14]的计算结果进行了比较，如表2所示。由表1 可知：随着初始横摇角的增大，阻尼系数识别质量逐渐变差，相比于一阶阻尼项系数而言，二阶阻尼项系数识别受初始横摇角的影响更为敏感，表现在其相对误差出现时对应的横摇角更小，且相对误差值更大。同时由表2 的对比可以看出：无论是对小初始横摇角还是大初始横摇角，文献[14]的阻尼系数识别值均存在相对误差。而本文方法的识别结果在初始横摇角不大于0.6 rad 范围内，均能够较为精确地识别出一阶和二阶阻尼系数，识别误差不大于0.03%；在大初始横摇角度时，本文阻尼系数识别精度明显高于文献[14]，如在最大横摇角0.866 rad 的初始条件下，本文的一阶和二阶阻尼系数识别误差分别为0.26%和0.415%，而文献[14]给出的阻尼系数识别误差分别为1.22%和1%，本文方法的一阶和二阶阻尼系数识别误差仅为文献[14]的0.21倍和0.42倍。

表1 不同初始横摇角下（33）式的阻尼系数识别结果Tab.1 Estimation of damping coefficients from Eq.(33)under different initial roll angles

同时，选取如下船舶横摇方程进行研究[5]

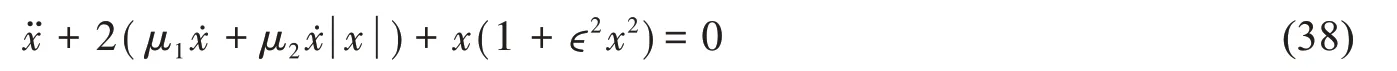
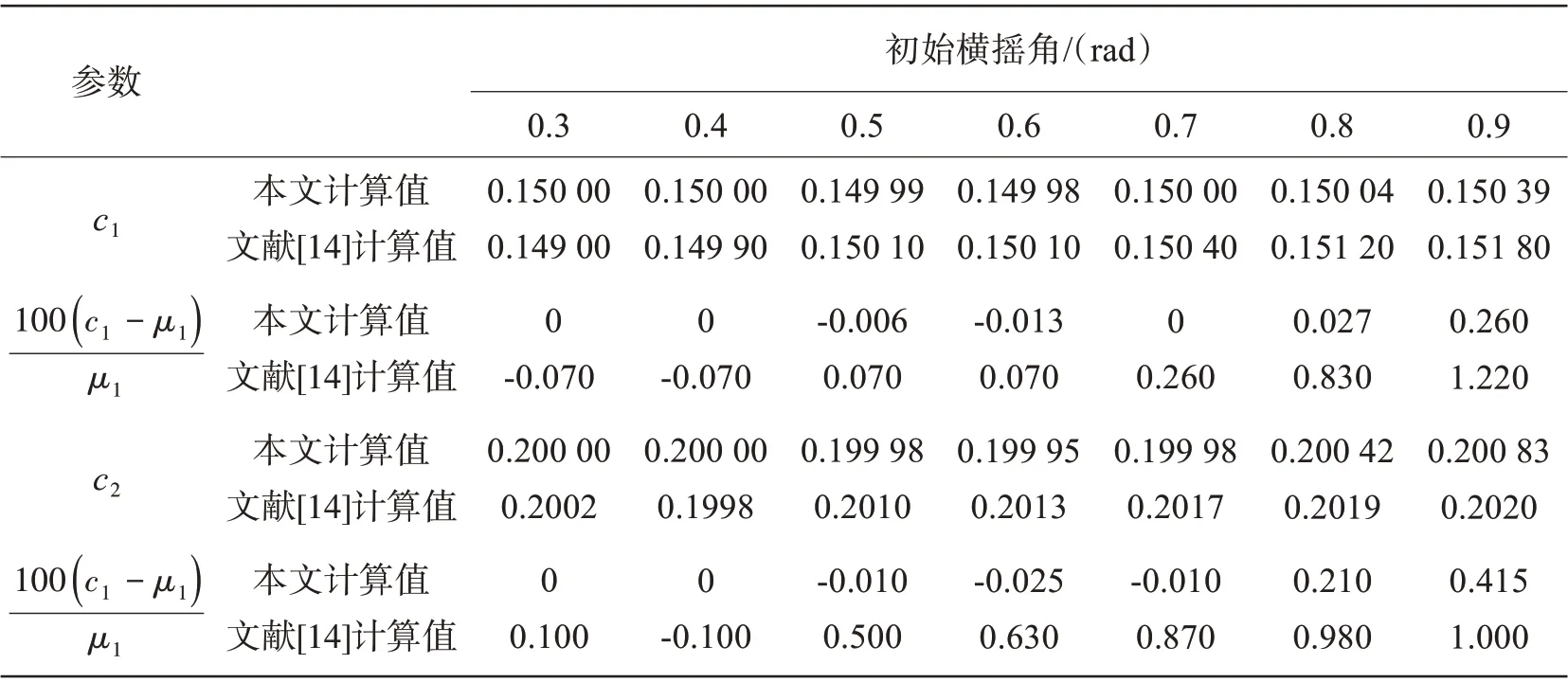
表2 本文识别的阻尼系数与文献[14]结果比较Tab.2 Comparison of the present work and the results from Ref.[14]

4 实例分析

将本文阻尼系数识别方法应用到实际船舶横摇衰减数据中。船模试验得到的横摇角峰值如表4所示[5]，船模的自摇横摇周期为2 s，对应实船的船模回复力矩为g( x )= 9.87x + 0.001 974x3。阻尼模型选用线性加二次阻尼模型，于是船舶模型的横摇运动方程如下：

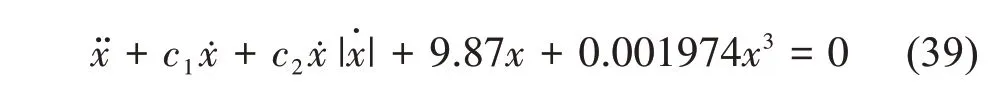
根据回复力矩表达式，可求得Φ0( a,φ )的表达式

计算得到（23）式中拟合系数p11=0.500 0,p12=0,q11=0,q12=1.333 4；由横摇衰减峰值数据可得到船模的横摇消灭曲线，进行数据拟合计算得到（27）式中拟合系数λ1= 0.678 4，λ2= 0.073 9。

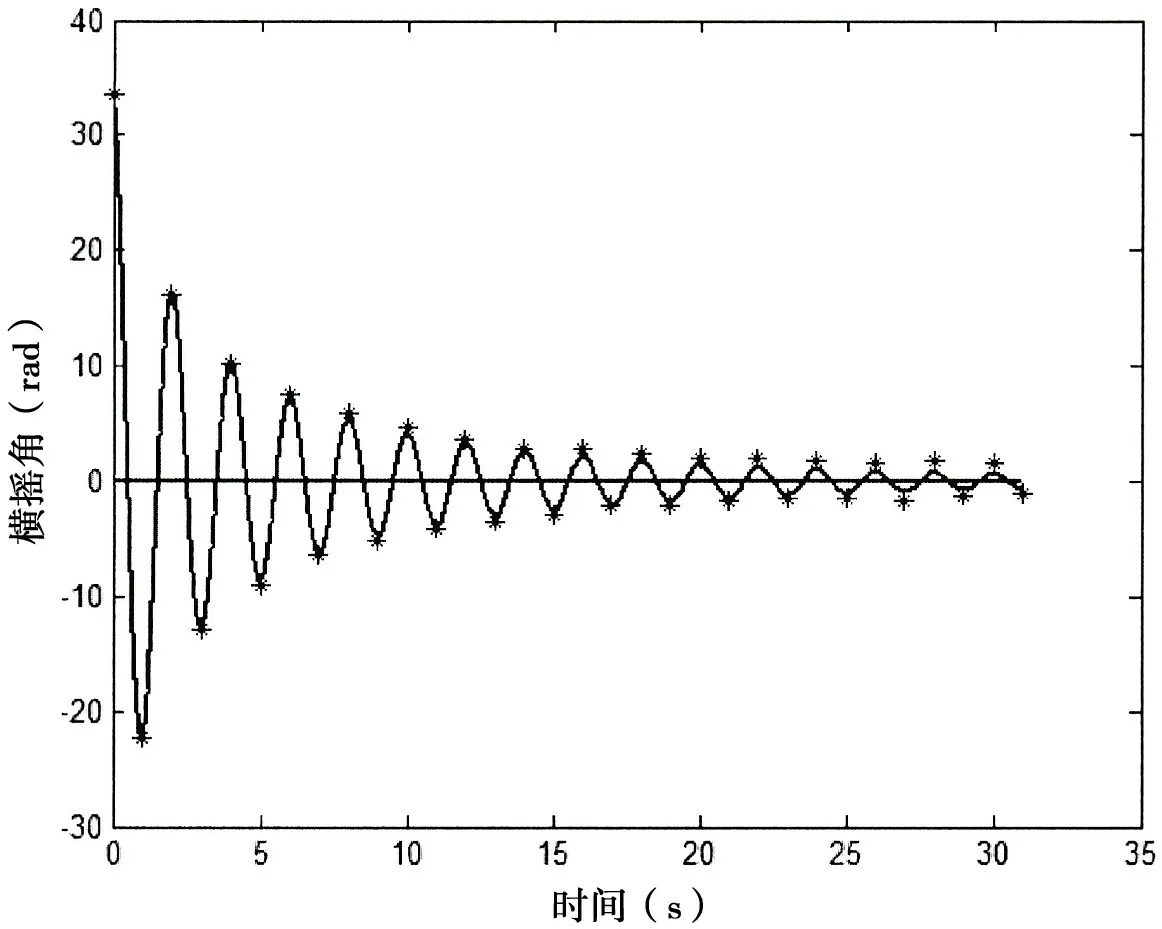
图4 模拟的自由横摇衰减曲线和试验峰值数据比较Fig.4 Comparison of experimental data on free-roll decay motion with the numerically simulated results

根据（28）式，可得阻尼系数c1和c2的第一次估算值= 0.147 9 和= 0.508 8。重复前文所述计算流程，得到阻尼系数最终估算值c1= 0.138 7，c2= 0.528 2。将该阻尼系数代入到（39）式中，通过数值模拟得到自由衰减曲线，并与衰减试验峰值数据进行比较，对比结果见图4。由图4 可知，本文估算得到的横摇衰减曲线峰值与船模试验得到的横摇峰值吻合较好，进一步验证了本文方法的有效性。

5 结 论

本文基于渐进理论，发展了一种利用试验衰减曲线进行非线性横摇阻尼系数识别的方法。通过数值仿真模拟及与已有研究成果的对比分析研究，验证了本文提出的阻尼系数识别方法的有效性和高精度，最后将该方法应用于实际船舶算例，模拟计算得到的自由衰减结果与试验数据吻合较好。通过本文的研究，可以得到以下结论：

（1）仅需要自由横摇衰减曲线峰值数据，利用本文提出的阻尼系数识别方法可精确估算出非线性横摇阻尼系数；

（2）本文提出的非线性阻尼系数识别方法适用于强非线性的回复力矩情形，回复力矩可以是任意形式奇次多项式函数；

（3）本文提出的非线性阻尼系数识别方法适用于大角度横摇，且具有较高的识别精度。虽然随着初始横摇角幅值的增大，阻尼系数识别质量下降，二阶阻尼系数的识别误差相对更高、出现误差时对应的初始横摇角度也更小。但是在最大回复力矩对应的横摇角范围内，一阶和二阶阻尼系数识别的相对误差仍非常小，在可接受范围内，特别是在小角度初始横摇角幅值条件下，阻尼系数的识别误差接近为零。