基于智能用电环境下家庭电力能效评估方法

薛冰， 杨祥勇， 李伟华， 魏恩伟， 王荣明

(1.深圳供电局有限公司， 深圳 518001； 2.深圳市康拓普信息技术有限公司， 深圳 518034)

0 引言

随着我国能源建设以及智能电网的普及，越来越多的个人以及企业对于电力能效指标进行关注，而我国政府以及电力部门通过对节能降耗指标体系的研究，目前也取得了显著成果，但是随着我国居民用电的逐年增加，居民用电能效评估体系目前并未取得突破性研究，家庭电能消耗的管理依然面临着缺乏完整体系，评估结果难以全面反映能耗情况等相关问题。因此针对家庭用电的相关问题，本文从我国东南沿海某市级城市的居民小区出发，研究该小区内居民用电数据，根据该数据设计出一套比较全面的家庭能效评估体系，从而敦促居民更为高效的使用现有电力。

1 相关理论

1.1 模糊综合评价法

模糊数学起源于1965年，其是由美国加利福尼亚大学机电工程与计算科学系交手，扎德所创立，该方法用精准数学成功的描述了模糊数学的概念，从而也宣告了模糊数学的诞生。本文选用的模糊综合评定法，源于背景师范大学数学数学系汪培庄先生的模糊综评定法，并且根据电力系统具体情况加以应用。其具体实施步骤如下：

1)确定评价对象的因素集

设U={u1,u2,…,um}为刻画被评价对象的m种评价因素(评价指标),其中:m是评价因素的个数,有具体的指标体系所决定。

为便于权重分配和评议，可以按评价因素的属性将评价因素分成若干类,把每一类都视为单一评价因素，并称之为第一级评价因素。第一级评价因素可以设置下属的第二级评价因素,第二级评价因素又可以设置下属的第三级评价因素,依此类推。

2)确定评价对象的评语集

设V={v1,v2，…,vn}，是评价者对被评价对象可能做出的各种总的评价结果组成的评语等级的集合。其中：vj代表第j个评价结果，j=1,2,…,n。n为总的评价结果数。一般划分为3～5个等级。

3)确定评价因素的权重向量

设A=(a1,a2,…,am)为权重(权数)分配模糊矢量，其中ai表示第i个因素的权重,要求0≤ai,Σai=1。A反映了各因素的重要程度。在进行模糊综合评价时，权重对最终的评价结果会产生很大的影响，不同的权重有时会得到完全不同的结论。现在通常是凭经验给出权重，但带有主观性。本文中权重向量的确立选取了10名电力系统工作员工，对于四个影响因子进行评级，最后去掉每项最高分，每项最低分其余部分求取平均值，最后四舍五入而成。

4)确立模糊关系矩阵R

单独从一个因素出发进行评价，以确定评价对象对评价集合V的隶属程度，称为单因素模糊评价(one-way evaluation)。在构造了等级模糊子集后，就要逐个对被评价对象从每个因素ui上进行量化，也就是确定从单因素来看被评价对象对各等级模糊子集的隶属度，进而得到模糊关系矩阵：

5)多指标综合评价

利用合适的模糊合成算子将模糊权矢量A与模糊关系矩阵R合成得到各被评价对象的模糊综合评价结果矢量B。

模糊综合评价的模型为：

(b1,b2,…,bn)

其中：bj表示被评级对象从整体上看对评价等级模糊子集元素vj的隶属程度。

6)对模糊综合评价结果进行分析

模糊综合评价的结果是被评价对象对各等级模糊子集的隶属度，它一般是一个模糊矢量，而不是一个点值，因而他能提供的信息比其他方法更丰富。对多个评价对象比较并排序，就需要进一步处理，即计算每个评价对象的综合分值，按大小排序，按序择优。将综合评价结果B转换为综合分值，于是可依其大小进行排序，从而挑选出最优者。

1.2 层次分析法确定权重

求权重是综合评价的关键。层次分析法是一种行之有效的确定权系数的有效方法。特别适宜于那些难以用定量指标进行分析得复杂问题[11]。它把复杂问题中的各因素划分为互相联系的有序层使之条理化，根据对客观实际的模糊判断，就每一层次的相对重要性给出定量的表示，再利用数学方法确定全部元素相对重要性次序的权系数。其具体实施如下：

1)确定目标和评价因素

P个评价指标，u={u1,u2,…,up}。

2)构造判断矩阵

判断矩阵元素的值反映了人们对各元素相对重要性的认识，一般采用1—9及其倒数的标度方法。但当相互比较因素的重要性能够用具有实际意义的比值说明时，判断矩阵相应元素的值则取这个比值。即得到判断矩阵S=(uij)p×p。

3)计算判断矩阵

本文选用MATLAB软件计算判断矩阵S的最大特征根λmax，及其对应的特征向量A，此特征向量就是各评价因素的重要性排序，也即是权系数的分配。

4)一致性检验

2 电力能效评估体系建立

本次研究以我国东南沿海某市级城市的开发区某大众小区为研究对象，该小区目前装配有可以提取用户每日用电信息的智能电表。小区入住率超过95%，调查对象具有普通家庭用电的基本特征。

2.1 因素论域确立

按照我国当今电力缴费制度通常以月为周期，对于居民用电进行电力缴费结算，而随着当今科技的发展，智能电表已经可以提取出用户每日的用电量信息，因此本次研究以用户每月单日用电平均质量为基础进行研究，故本次评价对象集为：

P=用户每月单日平均用电质量

2.2 评价因子选取

通常来讲，影响用户家庭用电的因素较多，但是如果将客户所有家电信息进行登记当前形势来讲，有些不符合目前国情。而从居民用电的根本来看，居民用电的本质在于舒适和方便，因此从这一角度出发，本次选取4个评价因子组成本次调查的评价因子集，其分别为：居民单日平均用电；居民高温天气单日平均用电；居民阴雨天气平均用电；居民单日最大用电。

居民单日平均用电该指标可以涵盖出用户常用用电设备的基本使用情况，例如，冰箱，电饭锅、照明设备等相关设备，这些设备的使用于居民来说，每月用电量基本固定，上下幅度相差不会太大，故可以在用户单日平均用电来表示。

其中居民单日平均用电计算方式为：

A1-居民单日平均用电；a-居民单日用电；i-当月具体日期；j-当月总体日期

通常，空调作为居民用电的一大主要耗电设备之一，但是其使用于居民来说有着一定的条件，由于本次调查属于东南沿海地区，以高温天气为主，因此空调的使用以大多用来制冷，因此本次研究根据其特点，单独列出高温天气的日平均用电情况，该指标可以在一定程度上显示出用户对于制冷设备的使用情况，例如空调、电扇等设备。

居民高温天气单日平均用电计算方式为：

A2-居民高温天气平均用电；a-居民单日用电；i-当月具体日期；k-当月高温日期

于居民来讲，由于阴雨天气客户大多会选择于室内活动，因此室内活动中家庭娱乐设施的使用会增加，如电视、电脑等相关设备，因此本次研究选取居民阴雨天气单日用电为指标，其具体计算方式为：

A3-居民阴雨天气平均用电；a-居民单日用电；i-当月具体日期；l-当月阴雨日期

居民最大用电表示，当月内居民用电最高的一日，该指标通常表示，用户使用了某些特殊用电设备，例如电烧烤架、家庭音响等设备，该项指标的具体计算为：

A4=MAX(ai)

A4-居民当月最大用电；a-居民单日用电；i-当月具体日期；

故本次评级因子的集合为：

A={A1;A2;A3;A4}={居民单日平均用电；居民高温天气单日平均用电；居民阴雨天气平均用电；居民单日最大用电}

2.3 评论域设定

根据居民用电的实际情况，本次设定将用户用电划分为A、B、C、D、E，将居民用电划分为5个等级，A表示优秀能效；B表示良好能效；C表示一般能效水平；D表示较差能效水平;E表示远极差能效水平。

4)权重计算

根据4个评价因子，构造判定矩阵S=(uij)p×p，即：

最终经过归一化处理后，权重因子为(0.05,0.35,0.15,0.45)

2.4 相关校验

使用MATLAB计算矩阵S的最大特征根，其计算结果为λ=4.004 59；

故其判定矩阵一致性CI为：

而通过查表可得，平均随机一致性RI=0.9；故随机一致性比率为：

由于0.001 7<0.1，因此本次层次分析结果一致性令人满意，故本次权重系数分配合理即权重分配有效。

3 相关应用

本次研究以我国东南沿海地区某小区内某单元楼5层整层10户为例，对于其2018年6月的的整体用电情况进行研究，其具体数据如表1所示。

表1 居民用电数据

根据2018年6月相关信息，该月具有30天，因此居民单日平均用电量计算中j，取30，故可计算各户中单日平均用电其具体结果如表2所示。

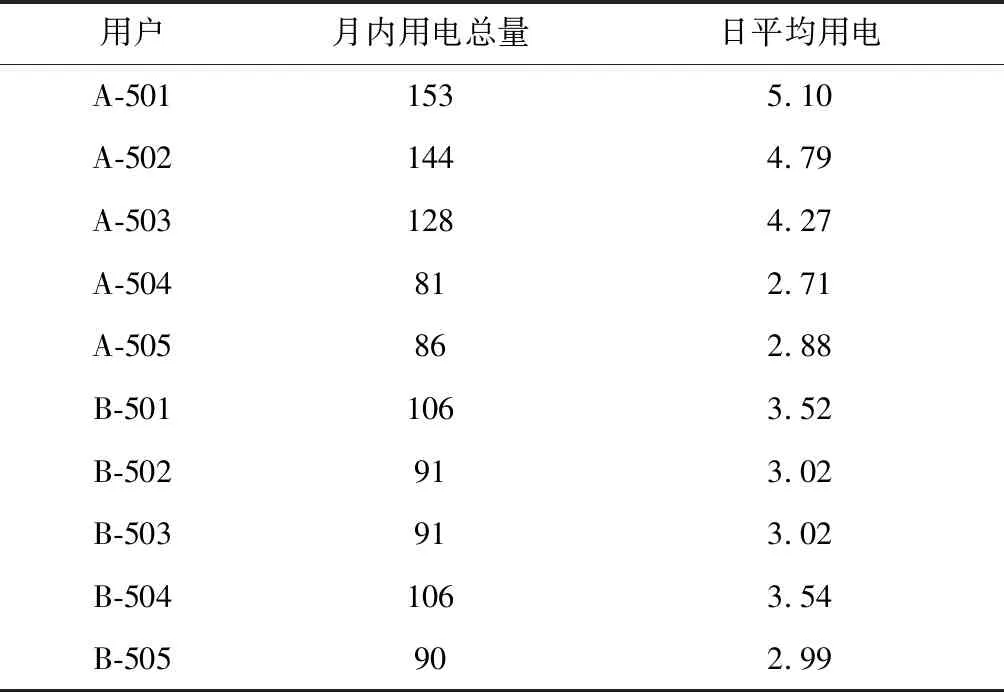
表2 居民用电数据

2018年6月，该地区温度超过31度的天气为25天，阴雨天气(不包含阵雨)为19天，故其高温天气单日平均用电与阴雨天气单日平均用电如表3所示。

表3 居民用电数据

将所有参数分别乘以对应权重后，最终得到用户用电质量评估表如表4所示。

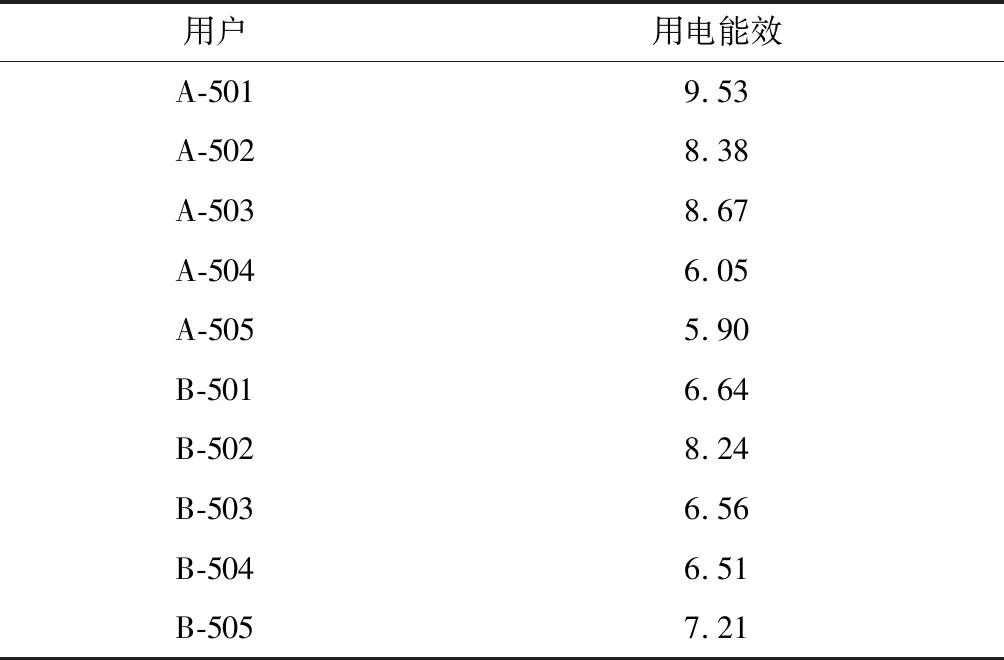
表4 居民用电数据

通过之前计算，最终结果小于6为A级，6～7为B级，7～8为C级，8～9为D级大于9为E级，故其最终评级如表5所示。

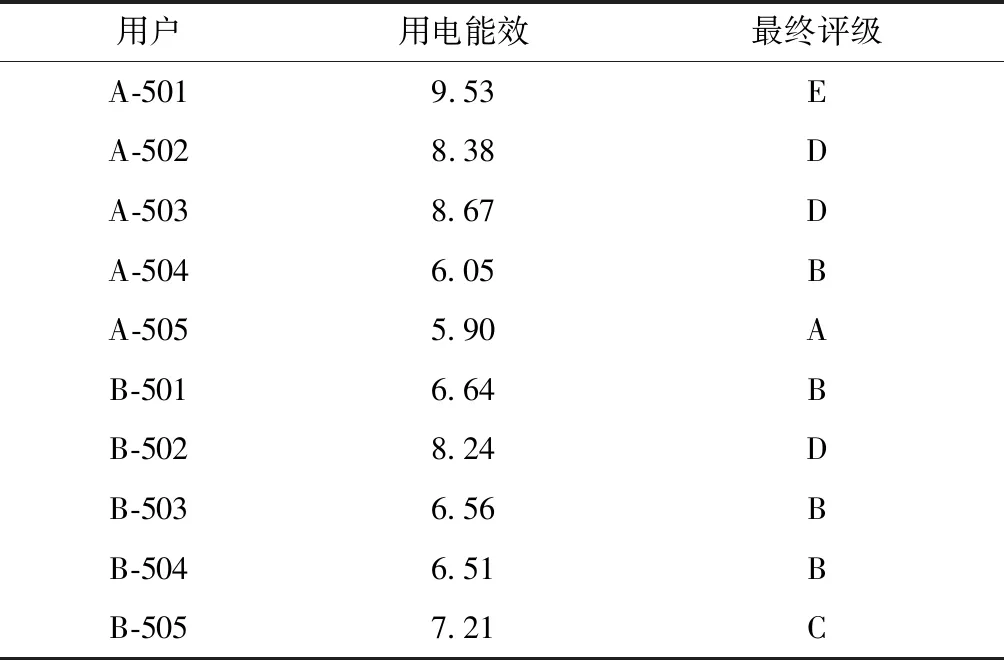
表5 居民用电数据评级

而最终经过笔者暗访，发现居民A-501，为某家庭旅馆，居室内空调超过4个，且经常处于24小时开放状态；评级为D的居民大多为与父母同住的家庭，家庭人口较多，用电情况复杂；B，C为普通上班族，家庭用电情况大同小异，受家庭用电设备中用电器械的品牌以及年限影响较大；评级为A的家庭家里节能设备超过了50%。

4 总结

本次研究通过建立家庭电力能效评估体系，反应了该体系下，东南沿海地区居民用电能效的基本情况，通过层次分析法以及模糊综合评定法，将家庭用电划分为5个等级，为我国即将实行的分段计价的电力收费形式提供了一种思路，同时该体系由于其采集数据较为简单，对于居民用电信息的搜集均通过智能电表采集而来，减去了居民具体信息带来的主观影响，方案简单易行。但是由于笔直能力有限，该模型有待进一步加强，例如对于我国北方地区来说，冬季暖炉的使用在该模型中并没有给出，同时，该模型只适合与普通居民小区，而对于高档居民小区部分用电情况并不在考虑范围内如高档小区内私人大功率用电设备等。