基于优化免疫算法冷链物流配送路径研究

施文嘉, 邵竑湄, 唐迪, 胡书红

(国网浙江省电力有限公司 电力科学研究院, 杭州 310000)

0 引言

国内外许多研究学者就冷链物流配送路径的优化进行了广泛关注[1-4]，其中的要点与难点就在于车辆路径的合理选择问题。很多研究学者提出通过算法来解决这一问题，其中精确算法无法解决大规模车辆配送路径的选择处理问题，只善于求解小规模车辆问题[5]；后来提出的启发式算法[6]很好的解决了这一难题，但是又出现了收敛速度慢，易早熟等问题；为克服这一缺陷，通过对算法进行改进提出了遗传学算法，但是遗传学算法在解决车辆配送路径优化问题上存在效率低下的情况[7]。基于以上考虑，本文提出了基于优化免疫算法来解决冷链物流配送路径优化问题。该算法使用广泛，操作便捷，实用性强，结合城市路网，构建冷链物流配送总成本最小数学模型，同时，对冷链物流配送路径优化问题进行建模研究。

1 冷链物流配送路径模型

生鲜产品在物流配送过程中，80%的损耗都是发生在运输配送环节。从节约成本的角度出发，优化配送路径是降低冷链物流成本的突破口。在配送过程中一是有车辆油耗，二是有区别普通常温配送的能源消耗。另外一方面，时间是影响货物新鲜程度的最关键指标，相比于普通常温配送，冷链物流由于产品本身具有的易腐性特点使得对冷链物流配送中的时间窗要求更为严格，这样也就造成了产生惩罚成本的几率大大增加。

1.1 问题描述

冷链物流配送路径优化问题可以描述为：

1) 配送中心以及客户的地理位置已知，配送中心有多辆车，且每辆车都配有冷冻、冷藏设备。

2) 从配送中心出发，用m辆车向n个客户进行货物配送，客户到配送中心的距离为d0j(j=1,2,…,n),客户之间的距离为dij(i,j=1,2,…,n)。每辆车的额定载荷是已知的，为wi(i=1,2,…,m)，客户对货物的需求量是确定的，为ci(i=1,2,…,n)，并且ci≤wi。

3) 根据客户的要求以及时间安排合理安排车辆进行货物配送，使配送总成本最小。

1.2 模型假设以及约束条件

在对实际问题进行解决的过程中，有一些条件无法同时满足，为简化问题的处理描述，需要在进行数学模型构建前进行一些条件假设与约束。

模型假设：

1) 配送中心只有一个；

2) 一个配送中心可以同时为多个客户提供服务，且货物能够满足所有客户的需求，同时配送中心的运输能力足以调配；

3) 车辆的自重不应超过其额定载荷；

4) 车辆的最大行驶距离是确定的;

5) 在运输过程中车内温度保持不变，同时车辆在行驶过程中及打开车门时的货损系数固定。

分配方案必须符合以下基本约束条件：

1) 在每个分配路径上，所有客户的总需求不超过分配车辆的额定负载；

2) 配送路径的长度不超过分配车辆的最大行驶里程；

3) 每个客户的货物由一辆配送车进行配送服务;

4) 对每个客户的配送时间都必须在约定的时间窗内。

1.3 数学模型

冷链物流配送总成本包括固定成本、运输成本、运输过程中的货损成本、开车门的货损成本、冷链配送惩罚成本以及制冷成本。

为了构建数学模型，假设zp是由第p辆车服务的客户数；使用集合Sp来表示第p辆车的路线，其中元素spi表示客户i在第p辆车配送路线中的顺序，sp0=0作为配送中心。

1) 包括折旧费，人工费等配送车辆的固定成本为式(1)。

C1=mf

(1)

其中，f是指每辆车的固定成本。

2) 与车辆的行驶的总路程成正比的运输成本为式(2)—式(8)。

(2)

约束条件：

(3)

0≤zp≤np=1,2,…,m

(4)

(5)

Sp={spi|spi∈{1,2,…,n}i=1,2,…,zp}

(6)

Sp1∩Sp2=Ø ∀p1≠p2

(7)

其中，

(8)

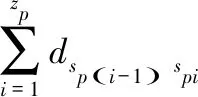
3) 即使运输过程中保持低温环境，依旧会造成生鲜产品一定的变质损耗。运输过程中的货损成本为式(9)。

(9)

其中，a为运输过程中的货损系数，g为货物的价格，vip为0,1 变量，若第p辆车为i客户提高服务，则vip=1，否则vip=0。

4) 打开车辆车门时，车内冷空气会和外界热空气进行交换对流，造成车内温度升高，造成生鲜损耗。开车门的货损成本为式(10)。

(10)

其中，b为打开车门的货损系数，Ri为每个客户的货物需求量。

5) 冷链配送惩罚成本

客户对时间有一个要求的到达时间窗[mi,ni]，还有一个可接受的时间窗[Mi,Ni]，[mi,ni]⊂[Mi,Ni]；当到达客户i的时间ti早于Mi，则需等待到Mi才能完成配送，这期间产生的货损该系数仍然为a；当到达客户i的时间ti在Mi与ni之间，则不需要惩罚。当到达客户i的时间ti在ni与Ni之间，则需付出一定的惩罚成本，惩罚系数为β。当到达客户i的时间ti晚于Ni，则提供服务不成功，惩罚成本为该客户需求货物的总价格。冷链配送惩罚成本的表达式为式(11)。

(11)

6) 制冷成本为式(12)。

(12)

其中，pf为制冷剂单价，F为制冷剂消耗量，tsp(i-1)spi为第p辆车从客户(i-1) 到客户i所用的时间。

综上，冷链物流配送总成本最小数学模型表示如式(13)。

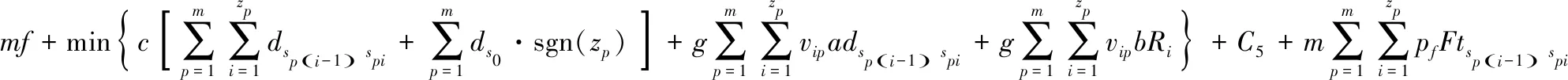
(13)

2 免疫算法模型理论

2.1 免疫算法原理

免疫算法是模拟生物免疫系统抗原抗体而生成的一种新型智能计算方法。免疫系统由抗原识别系统、记忆系统、抗体的加速和控制机制等组成，通过细胞分裂产生大量的抗体来抵抗各种抗原。免疫系统有很强的学习能力、识别能力及记忆能力，能够辨别外界的有害信息，保证系统的安全稳定性。并且免疫系统具有保持群体多样性的特点，因此免疫优化算法能够有效克服在寻求最优解的过程中出现的“早熟”问题[8]，从而获得全局最优解。

免疫算法流程图如图1所示。

实现步骤如下所示：

1) 分析问题。本文的研究目的是合理地确定配送车辆与客户之间的关系，在满足客户需求、车辆载荷、时间窗等的约束条件下，求出最低总成本。

2) 抗原识别。本文将采用抗体与抗原之间的亲和力大小来进行识别。

3) 产生初始抗体群。以随机产生的抗体及记忆库存储的抗体作为初始抗体群。

4) 抗体评价。本文将对每个抗体进行评价。

5) 形成父代种群。按照个体期望繁殖概率进行排序，排名靠前的N个个体将被选作父代种群，并选取其中的m个放入记忆库。

6) 判断结束与否。满足条件结束，否则进行下一步。

7) 新种群的产生。新种群由两部分构成，父代选择、交叉、变异等操作形成一部分，再从记忆库中取出来形成另一部分。

8) 新一代种群形成之后进行循环操作。

2.2 优化算法操作流程

在免疫算法对配送总成本最低的求解过程中，以目标函数和约束条件为抗原，以其浓度为抗体。在免疫过程中，一些抗体作为记忆细胞被保留下来，当同源抗原再次攻击时，记忆细胞会迅速爆炸产生大量抗体，产生更快的响应。同时，免疫系统具有自我调节功能，能维持抗体的多样性和免疫系统的平衡[9]。

算法操作流程如下：

1) 抗原输入和抗体编码。

输入抗原：目标函数和约束条件。

为方便研究，减少无效解的产生，采用自然整数进行编码，形成抗体序列码。对n个客户进行编号，则路线可形成长度为n的抗体。如n=6,则抗体为(2，4，6，5，3，1)，此抗体序列码即表示，从配送中心0出发，依次配送客户2→4→6→5→3→1后，返回配送中心0，形成一条配送路径。

2) 初始抗体群的产生

首次选择时，抗体随机选择。之后，部分初始抗体通过免疫系统的记忆功能从记忆库中获得，其余部分再由系统随机生成[10]。由于记忆库中的抗体具有较高的适应度和较好的物种分布，因此可以提高收敛速度。

3) 亲和度的计算

抗体与抗原间的亲和度表示抗体对抗原的识别程度，当抗体遇到抗原时，它们越亲和，那就越接近最优解。本文的亲和力函数表示为式(14)。

(8)

其中Yi为冷链物流配送路径优化的目标函数。

这样就将最小值问题转化为目标函数的最大值问题。

抗体与抗体间的亲和度代表抗体之间的相似程度，抗体间的亲和度表示为式(15)。

(15)

其中si,s表示两个抗体间相同的位数，L表示抗体的长度。L的长度由配送的客户的数量决定，如两个抗体分别为(1，6，5，3，2，4)和(4，7，6，5，8，9)，两个抗体有3个相同位数，则亲和度为0.5。

4) 抗体浓度的计算

抗体浓度代表相似抗体在整个种群中所占的比例。当抗原或者新抗体攻击免疫系统时，免疫系统将产生激烈反应，产生大量抗体。随着抗体的增加，其亲和力就会上升。达到一定程度时，其浓度就会降低[11]。即在优化过程中，会导致优化停滞，并收敛过早。

抗体浓度表示为式(16)。

(10)

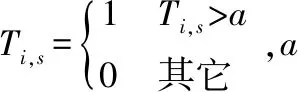
5) 期望繁殖概率：促进和抑制抗体产生

期望繁殖概率由抗体与抗原之间的亲和度及抗体浓度来表示，期望繁殖概率Pi表示为式(7)。

(17)

从上式可以看出个体适应度与期望繁殖概率成正比，个体浓度与期望繁殖概率成反比。这样就既可以鼓励高适应度的个体的产生，又可以抑制高浓度个体的产生，从而保证个体的多样性。

6) 交叉变异操作

群体更新的方法与遗传算法基本相同。本文采用轮盘赌选择机制进行选择操作，个体期望繁殖概率即个体被选择概率。采用多点交叉的方式进行交叉操作，从交叉操作中产生的抗体群中随机选择变异位进行变异操作产生新的个体[12-13]。

3 算例分析

3.1 问题描述

本文以武汉某生鲜配送公司为例，对冷链物流配送路径进行研究。该公司共有3辆车，对9个市内生鲜批发市场进行生鲜配送供应。每辆车额定载量均为w=4t,各参数数值如表1所示。配送中心与各批发市场之间、各批发市场之间的距离(km)及各批发市场货物需求量(t)如表2所示，0代表配送中心，市场时间窗如表3所示。

表1 各参数数值

3.2 优化免疫算法求解冷链物流最短配送路径

通过理论分析及数学建模，基于免疫优化算法求解冷链物流配送路径最优问题，可以通过编程实现，并通过对结果的分析，验证了算法的有效性。

初始代生成是随机的，给定群N=40，最大进化代数G=200 ，码长L=27 ，交叉概率Pc=0.7，突变概率Pm=0.1。根据时间窗要求，预先设定客户9为第一条线路的第一个客户。通过编程，输入约束条件，随机求解6次，结果，如表4所示。

从计算结果可以看出，计算到61代时，首次搜到最优解，配送最低成本为2015.58元,且适应度最高。配送路径各个车次都按照相应时间窗要求，将货物送到，惩罚成本为0。当前每辆车都达到85%以上的满载，但每辆车服务的客户较少，同时生鲜配送公司离各批发市场较远，这样就造成了在这段路程上成本的浪费。另外一方面，每个批发商之间的距离是比较近的，从批发商到批发商之间耗费时间是比较少的，我们可以通过合理安排时间窗，把运输车改为额定载量为5.5 t和6 t的货车，这样两辆车就能完成所有货物的配送，可以有效降低成本，减少资源浪费。

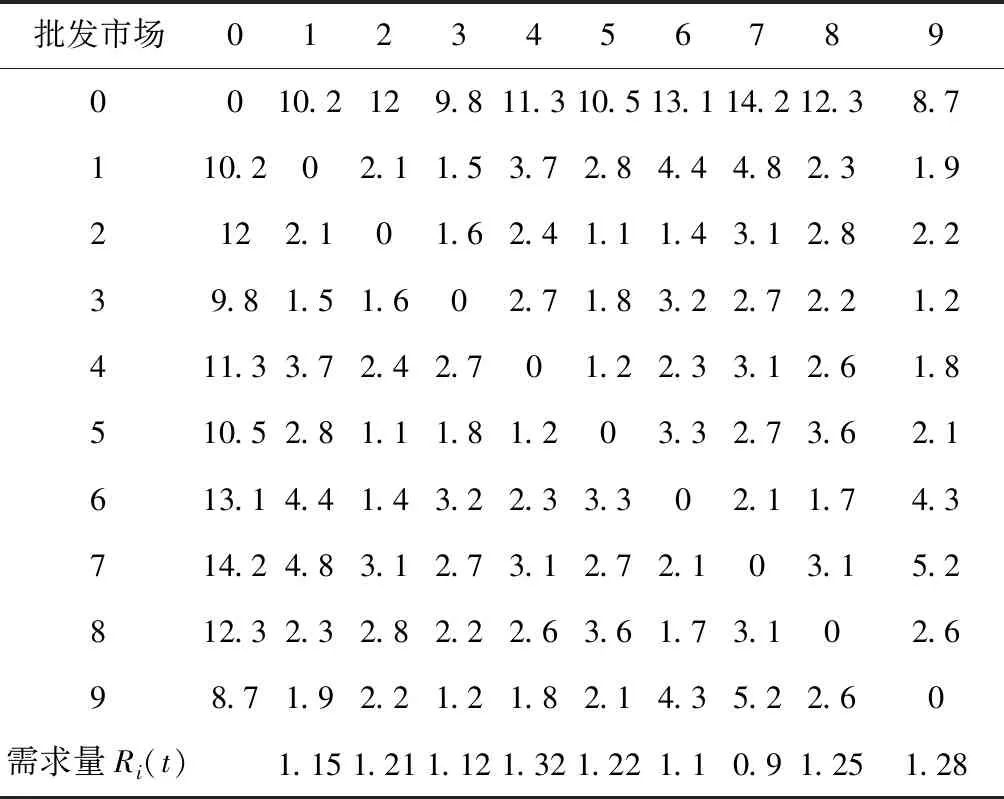
表2 配送中心与各批发市场之间、各批发市场之间的 距离及各批发市场货物需求量

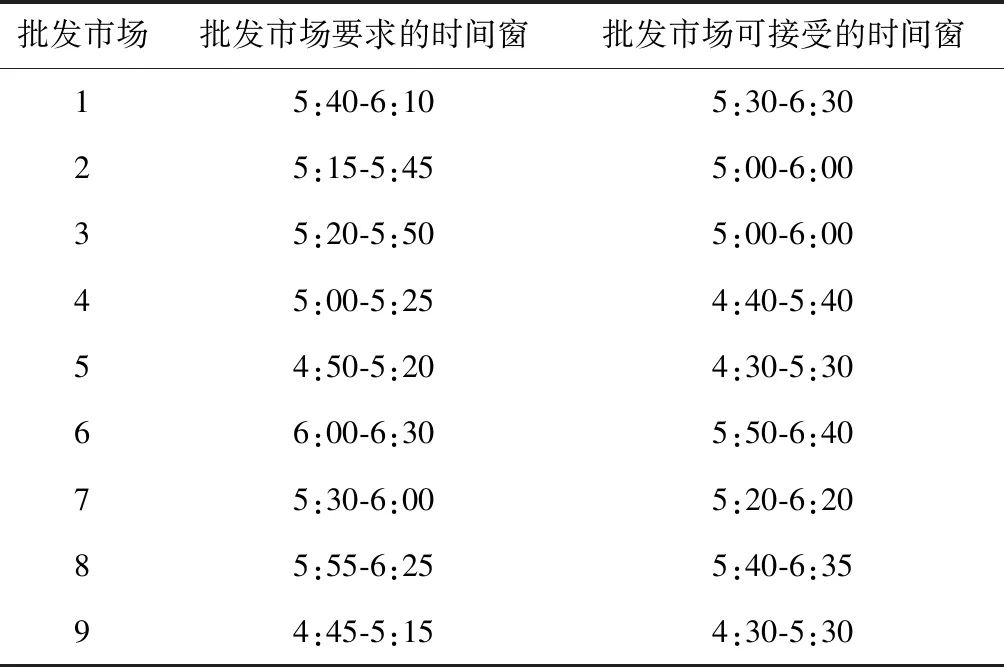
表3 各批发市场时间窗

表4 冷链物流配送路径优化问题的免疫优化算法求解结果

为:0→9→3→1→0; 0→5→2→6→0; 0→4→7→8→0;如表5所示。

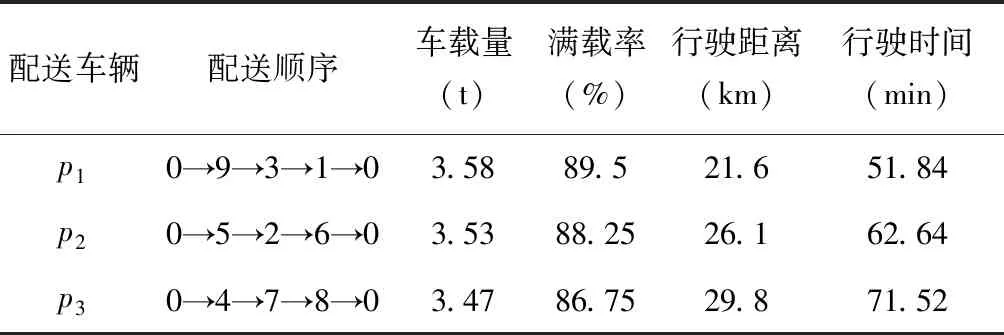
表5 配载情况表

由此可得，免疫优化算法可以方便有效地求得冷链物流配送路径的最优解，为实际应用进行指导。

4 总结

本文研究了冷链物流配送路径优化问题。基于免疫优化算法，通过数学模型的建立，加入时间窗及车辆载荷等约束条件，快速求得最优配送路径。通过对实列的分析，可证明免疫优化算法对冷链物流配送路径问题求解是合理有效的，免疫优化算法具有更高的收敛速度，没有半早熟收敛，并且它可以在短时间内搜索最佳路径。通过抑制高浓度的抗体并添加新的高适应度个体，免疫优化算法可以维持抗体的多样性。同时，免疫优化算法通过选择交叉和变异操作来保持良好的本地搜索能力，是一种有效的路径优化方法。最后在具体实例中提出了更为合理的路径安排方法，使得在配送过程中可以最大程度地节约成本，提升配送效率，保证生鲜产品的质量。