基于Lanchester方程的反舰作战效能评估方法

李海涛

(中国人民解放军91404部队43分队， 秦皇岛 066000)

0 引言

各国军方对装备作战效能评估方法和理论研究工作高度重视,积极探索创新,装备作战效能评估被广泛应用于新装备的研制开发、新战术战法的评估和装备模拟训练等领域,有效地促进武器装备的更新换代，推动了军事理论创新与发展，提升了部队战斗力[1]。

美军早在上个世纪60年代就开始研究武器装备系统的作战效能评估问题，评估的理论和方法日趋成熟，建立了较为完备的装备作战效能评估体系，在武器装备、作战研究和部队训练等领域被广泛应用，取得了良好的军事经济效益[2]。美军在装备作战效能评估方面取得的成功经验为个国军事人员所重视，其关于作战效能评估的理论与方法也为各国开展相关领域的研究提供了借鉴[3]。

1 反舰作战效能评估方法分析

现在反舰作战主要武器是反舰战术导弹，因此主要评估反舰导弹的作战效能。在反舰导弹武器系统效能评估中，无论是导弹武器系统的引导过程，还是水面舰艇反舰作战的对抗过程，均属于随机过程[4]。一般讨论的随机模型是根据反舰导弹武器系统具有的包含大量随机因素的规律，以概率论为基本数学工具，结合随机过程理论、模糊数学理论、人工智能理论、灰色系统理论和人工神经网络理论建立的，其结果通常也是在概率意义下表示出来的[5]。到目前为止，对武器系统作战效能进行评估的随机方法通常可分为统计试验法和解析法两大类[6]。

统计试验法具有通用性强、没有原理误差、以及精度结果可以预测和控制等优点。但是为统计出可信的计算结果它需要样本量较大，且获取这些样本的试验过程耗时较长。这样，在导弹武器系统这种对实时性、快速性要求较高的环境中，使用难度比较大[7]。

比较传统的解析法如英国人F.W.Lanchester建立的描述作战动态过程的Lanchester微分方程[8]。在该方程的基础上，W.PHannah和J.Tavantzis等人先后引入了作战过程的随机因素，建立了多种形式的随机类型Lanchester方程。另外，排队论，或称随机服务系统理论也是解析分析导弹武器系统效能进行评估的较为有效的工具。下面，重点讨论集中对导弹武器系统效能进行评估的较为成熟的解析法，即随机类型的Lanchester方程分析法、协方差分析描述函数技术和统计线性化伴随法[9]。

英国人F.W. Lanchester首先建立了描述作战动态过程的微分方程，并且该理论不断完善。利用该理论建立反舰导弹-舰艇防控火力对抗的确定型Lanchester模型，并以此到处随机类型的Lanchester方程[10]。

2 确定型Lanchester方程评估方法

在反舰导弹与水面舰艇反导火力系统的攻击与防御抗击的随机过程中，舰艇受损情况与单位面积上的舰载反导火力单元数量和攻击的导弹数量相关[11]，因此推导水面舰艇反舰作战的损耗方程时可做以下假设：

(1) 水面舰艇受损情况可近似符合Lanchester第二线性定律；

(2) 反舰导弹以Poisson分布随机地到达水面舰艇后，只攻击舰艇主体区域，舰载反导火力单元未受到毁伤；

(3) 水面舰艇舰载反导火控雷达对导弹的发现时间及火力单元单次设计时间均服从负指数分布，设分布参数为ξ，防控火力单元两次发射间隔时间期望为τ。

取b(t)为来袭的反舰导弹数量；r(t)为舰载反导火力单元数。则可得到舰载反导火力系统在τ时间内未发现任何来袭目标的概率为式(1)。

P0(τ)=e-ξτ

(1)

则在τ时间内b(t)个目标至少被发现一个的概率为式(2)。

P1(τ)=1-e-ξτb(t)

(2)

发现并击毁一枚导弹的概率为式(3)。

P=Pk·P1(τ)=Pk[1-e-ξτb(t)]

(3)

式中，Pk为反导火力系统 的单发杀伤概率。

τ时间内r(t)个反导火力单元杀伤来袭导弹的期望值为式(4)

E(b)=r(t)Pk[1-e-ξτb(t)]

(4)

反舰导弹是以参数为λ的Poisson分布随机来袭，假设t时刻导弹能够突防的概率为Pt，λpt则为导弹到达水面舰艇反导火力单元防御区域时的飞行速度，来袭导弹在反导火力单元防御区域数量变化可做如下推导，如式(5)[12]。

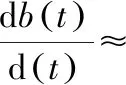
(5)

取AR为水面舰艇反导火力单元防御区域的总面积，rv为单个反导火力单元防御区域的半径，rk为单枚反舰导弹的有效毁伤区域的半径。水面舰艇若有r(t)个反导火力单元，一枚反舰导弹对该系统火力单元的杀伤概率为式(6)。

(6)

反舰导弹到达率为λ，则反导火力系统在b(t)枚导弹攻击下的损耗率为式(7)。

(7)

式(1)和式(2)即为水面舰艇反舰作战时攻防对抗系统的确定型Lanchester方程。

3 随机型Lanchester方程评估方法

在反舰作战过程中，设B(t)为t时刻反舰导弹数量的随机函数，设R(t)为t时刻水面舰艇火力单元数的随机函数，可得出反舰作战时攻防概率分布函数为式(8)[13-17]。

pb,r(t)=p[B(t)=b,R(t)=r]

(8)

对反舰作战过程进行分析得出，t+Δt时刻pb,r(t)动态方程为下述各独立事件的概率之和：

(1)t时刻处于状态(b+1,r)，在Δt时间内有一枚导弹被拦截或飞离火力杀伤区，该事件的概率为式(9)。

pb+1,r(t)=[Pk·ξ·r·(b+1)+λ·pt]Δt

(9)

(2)t时刻处于状态(b+1,r)，在Δt时间内有一枚导弹飞入火力杀伤区，该事件的概率为式(10)。

pb+1,r(t)=λΔt

(10)

(3)t时刻处于状态(b,r+1)，在Δt时间内有一个火力单元被击毁，该事件的概率为式(11)

(11)

(4)t时刻处于状态(b,r)，在Δt时间内没有导弹火力单元的数量变化，该事件的概率为式(12)

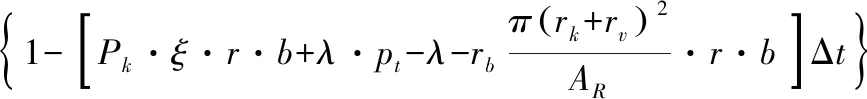
(12)

上述4式相加求导即可得到状态概率的动态方程，即基于Lanchester随机类型方程的反舰作战攻防对抗评估方程。针对该方程求解可得到任意时刻t对抗双方评估要素的概率pb,r(t)，对各要素进一步分析可得到任意时刻t水面舰艇反舰作战效能。下式即为在t时刻导弹能够突破防御火力系统的概率为式(13)[18]。

(13)

4 反舰作战效能评估方法

根据随机型Lanchester方程评估方法，可以推导出反舰导弹突防时作战效能评估方法，即反舰作战效能评估方法。推导步骤如下：

(1) 假设第一枚反舰导弹进入水面舰艇的反导火力范围是为作战起始时间，则反舰作战攻防对抗的初始状态则为：b(0)=1，r(0)=n；其中n为水面舰艇火力单元个数；随机型Lanchester方程初始值则为式(14)[19]。

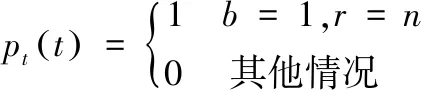
(14)

(2) 依据突防导弹数量及水面舰艇的反导火力单元数量排列组合，利用随机型Lanchester方程可得出不同导弹和反导火力单元数量情况下的反舰作战突防概率[20]。

(3) 根据随机型Lanchester方程可推导出突防概率分布函数pb,r(t)；对该函数求解可得出任意时刻t水面舰艇的反舰作战效能[21]。

5 总结

海战场是未来战争的主战场，水面舰艇是海军部队遂行海上作战任务的重要作战单元[22]。实践表明，做好反舰作战效能评估的研究，不仅可以减少作战训练经费、调高效率，而且对于加强海军装备建设、提高海军部队战斗力具有极为重要的意义[23]。