巷道围岩在爆破荷载下的反应谱特征研究

宋春辉，李祥龙,2，范天林，陈 浩，宋 飞

(1.昆明理工大学，昆明650093；2.云南省中-德蓝色矿山与特殊地下空间开发利用重点实验室，昆明650093；3.玉溪矿业有限公司大红山铜矿，云南 玉溪653405；4.四川路航建设有限责任公司，成都610000)

在对巷道围岩破坏调研中发现，爆破荷载下围岩破坏较为普遍，因而本文针对矿山复杂场地中爆破振动展开研究。随着震灾经验的不断积累，人们已经认识到地震动的频谱组成对巷道围岩的结构反应有着重要影响[1]。

早在1943年，美国学者Biot提出反应谱这一概念，现已广泛应用于结构体抗震领域。爆破地震反应谱理论是地震工程领域较为成熟的分析方法，该方法综合考虑了信号的频谱、幅值以及结构自身的动态特性[2]。20世纪50年代，我国开始初步研究爆破地震效应，至50年代中期，反应谱理论开始逐步应用在我国的抗震设计之中[3]。在工程爆破领域，越来越多的专家学者开始应用反应谱理论研究爆破振动[4]。

本文结合大红山铜矿现场实例，对现场的爆破振动信号进行检测，选择有代表性的振动波形为激励输入已经编好的MATLAB程序，对得到的爆破振动速度、位移、绝对加速度和绝对加速度标准反应谱曲线展开分析。

1 反应谱理论

反应谱理论是以单自由度黏性阻尼体系在实际爆破振动工程中的反应为基础[1,5]的反应谱理论对结构进行分析，利用应力谱计算建筑物的地震作用，不仅简单快捷其精度也能够满足要求[6]。反应谱分析方法能够客观反应结构体在爆破荷载下的损伤程度[7]，并且可以得到结构体在爆破作用下的动态响应[8]，行之有效的分析爆破振动对地下构建筑物的影响。

反应谱理论分析是在地震激励下分析结构动力的一种方法，基于结构的振动特性(固有频率、固有振型以及振型阻尼比)和反应谱表征的地面运动的动力特性[9]，此举既可以真实反映频谱特征也可以更加便捷得应用到工程结构抗震设计中[1]。

2 现场振动测试

本次进行现场波速测试使用NUBOX-8016爆破振动记录仪布置于460切顶巷围岩54～58线两侧，其仪器及具体参数如图1、表1所示；围岩力学参数如表2所示；现场布置示意图及所测围岩爆破振动监测数据如图2、表3所示。

图1 NUBOX-8016爆破振动记录仪Fig.1 NUBOX-8016 blasting vibration recorder

表1 技术参数

Table 1 Technical parameter

标准配置技术指标最高采样率2 000 kSpsA/D分辨率16 Bit量程±1 V、±2 V、±5 V、±10 V测量精度0.1%信噪比86 dB通道间相位差≤0.3°(0～10 kHz)通道间隔离度≥90 dB智能触发触发阀值自适应,无需设置数据存储最多可记录16 384次数据,单次最大数据长度为57 600样点供电方式内置电池供电或外部直流电源

表2 巷道围岩力学参数

图2 传感器现场布置示意图Fig.2 Sensor site layout diagram

表3 爆破振动监测数据表

Table 3 Blasting vibration monitoring data sheet

监测对象检测次数爆心距/m最大单响药量/kg振动速度/(cm·s-1)切向径向垂向围岩体(54～58线)1862 48611.747.9916.1221852 4868.426.116.5132908032.733.441.9345332 9631.871.711.1351081 0512.091.591.286961 1203.432.812.9773569801.240.960.5987567410.547.775.87

3 爆破振动反应谱曲线及分析

在最具有代表性的振动波形基础上选取X、Y、Z三个方向中显著的振动波形(即X方向)作为激励输入导入MATLAB程序进行运算分析。其中爆心距86 m的4#机振速为11.74 cm/s，爆心距185 m的7#机振速8.42 cm/s。4#机所测振速、加速度波形图见图3、图4。

图3 振动波形图Fig.3 Vibration waveform

图4 加速度波形图Fig.4 Acceleration waveform

7#机所测振速、加速度波形图见图5、图6。

图5 振动波形图Fig.5 Vibration waveform

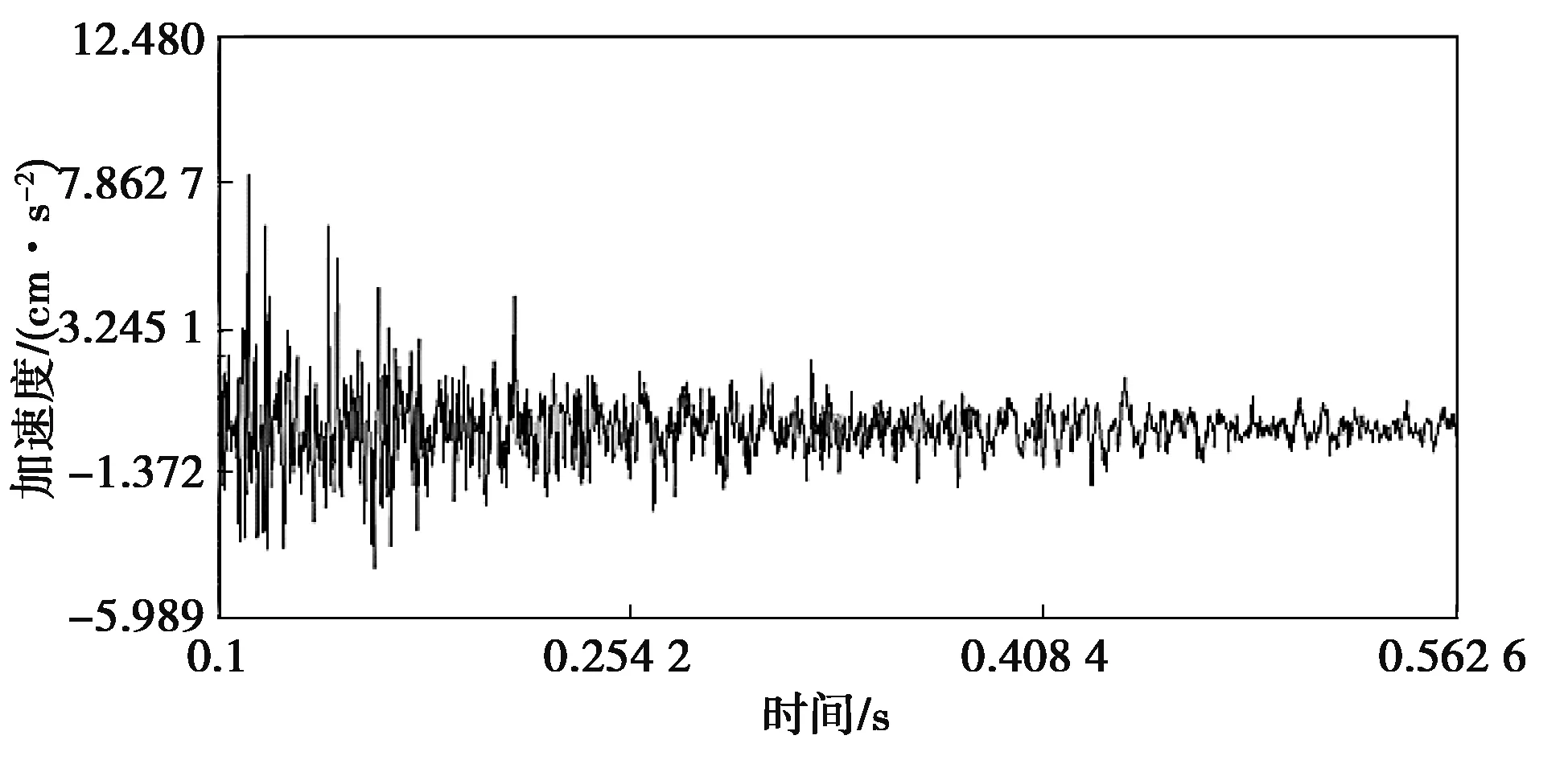
图6 加速度波形图Fig.6 Acceleration waveform

建筑结构的阻尼比ξ通常在0.02～0.05范围内，在建筑物减振降振过程中，阻尼起着关键性作用，故在工程抗震设计规范计算选取ξ=0.05[10]。本文选取阻尼比(ξ)为0.02、0.05、0.1下的反应谱进行分析，将以上所测得的波信号通过卷积分计算得到对应的反应谱曲线以此来分析阻尼比对结构体减震效果。

3.1 速度反应谱曲线分析

针对图7速度反应谱曲线分析得出以下结论：

1)由两测点的速度反应谱曲线可知，增大阻尼比ξ减震效果很显著。其中ξ=0.05～1区间范围内的速度反应谱峰值减小量小于ξ=0.02～0.05。

2)随着周期增大两测点所测得的速度反应谱曲线逐渐平缓，4#机的速度反应谱峰值主频率位于3～100 Hz；7#机的速度反应谱峰值主频率位于0.65～1 Hz。由此可见在爆心距86～185 m区间内，围岩中爆破振动主频在向低频方向发展。

3)在周期2 s内，7#机所呈现的速度峰值数明显多于4#机，且7#机大多数机速度峰值所对应的频率都在10 Hz以下，与巷道围岩自振频率更为接近。由此得出爆心距185 m的爆破振动比在爆心距86 m处更剧烈，随着爆破区域的扩展振动强度可能会减小，但这不代表巷道围岩稳定。

4)从爆心距86 m到爆心距185 m，爆破振动速度最大反应谱值有所减小，由爆破距86 m处的8.8 cm/s降到爆心距185 m处的4.3 cm/s，最终两曲线都趋于定值，与阻尼比的大小无关。

图7 速度反应谱Fig.7 Velocity response spectrum

3.2 位移反应谱曲线分析

针对图8位移反应谱曲线分析可知：

1)爆心距在86 m处的位移明显大于185 m处，位移变化量也更大。相比于速度反应谱最大峰值频带的尖窄，位移反应谱频带则显得更平缓，横跨周期更大。

2)两测点处的位移反应谱曲线形式都相对圆滑。爆心距185 m出现的波峰多于爆心距为86 m处，说明距离的增大会使质点位移出现频率带放大效应，其位移的幅值也会降低，位移波峰的多次出现也恰恰说明此处围岩更加不稳定。

图8 位移反应谱Fig.8 Displacement response spectrum

3.3 绝对加速度反应谱曲线分析

针对图9绝对加速度曲线分析可知：

1)绝对加速度主峰数较少，作用在围岩上的时间也比较短，同时加速度的数值也反应爆破振动对巷道围岩的影响程度。其中周期为0.1～0.2 s范围内，爆心距86 m处的加速度可达到几个到几十个重力加速度，远大于爆心距185 m处。与此同时阻尼比的作用显得更为关键，阻尼比对主峰的削减作用比较明显，阻尼比越大对应的加速度值则越小，两者成反比。

2)绝对加速度反应谱曲线在短时间内迅速达到峰值，随后急剧下降，通过对比图9与图7可知，加速度反应谱峰值周期与速度反应谱峰值周期并不相同。由此可见，速度、绝对加速度反应谱最大峰值频率相差较多。

3)为保证巷道围岩的稳定性，可以将计算所得的加速度最大峰值与围岩自身质量相乘计算出在爆破振动下围岩所受的最大剪应力，对巷道围岩的支护具有指导意义。

图9 绝对加速度反应谱Fig.9 Absolute acceleration response spectrum

3.4 绝对加速度标准谱反应谱曲线分析

为分析巷道围岩动力放大作用，故应用绝对加速度标准谱进行进一步分析爆破振动下巷道围岩动态响应特性。针对图10加速度标准谱分析可知：

1)通过4#机和7#机所测数据对比可知，在爆心距增加的过程中，绝对加速度标准谱主峰值放大倍数有所减小。

2)绝对加速度标准反应谱放大系数可直观的反应出爆破振动作用下巷道围岩的反应程度，在放大系数等于1时，巷道围岩与爆破振动频率基本一致，会出现共振现象，此时巷道围岩的安全将会受到很大影响。由7#机(爆心距为185 m)阻尼比为0.05对应的曲线可知，此时放大系数刚好为1，爆破振动作用很容易使巷道围岩发生损伤破坏，因此，必须要对此处围岩进行监测并采取必要的加固措施来确保井下安全。

图10 绝对加速度标准谱Fig.10 Absolute acceleration standard spectrum

4 结论

基于反应谱理论对巷道围岩中实测爆破振动信号进行振速、位移、绝对加速度以及绝对加速度标准反应谱曲线分析，得出以下结论：

1)爆心距为185 m的速度反应谱峰值数多于爆心距为86 m的速度反应谱，爆心距185 m出现的10 Hz以下的谐波分量多于爆心距86 m，爆破作用下爆心距185 m处的围岩损伤影响更大，在此范围内爆心距增加也并不代表巷道围岩稳定。

2)为保证巷道围岩的稳定性，可以将计算所得的加速度最大峰值与围岩自身质量相乘计算出在爆破振动下围岩所受的最大剪应力，这对巷道围岩的支护具有指导意义。

3)绝对加速度标准反应谱放大系数可直观的反应出爆破振动作用下巷道围岩的反应程度，爆心距185 m、阻尼比为0.05时放大系数为1，巷道围岩与爆破振动频率基本一致，会出现共振现象，此时巷道围岩的安全将会受到很大影响。