微机电系统麦克风灵敏度不确定性分析

刘 雷，贾仁需

(西安电子科技大学微电子学院陕西西安710071)

微机电系统是在微电子技术基础上融合硅微加工和精密机械加工等多种微加工技术，并应用现代信息技术构造的微型系统。微机电系统技术已经广泛应用于麦克风、开关、陀螺仪、加速度计、谐振器和可调天线等领域[1]。灵敏度是标准声学输入时微机电系统电容麦克风输出端机械或电气响应，是衡量麦克风性能的重要指标。影响微机电系统器件不确定性因素包括微机械结构性能退化和制造工艺造成器件表面形状不规则、残余应力与化学残留等[2-4]。传统微机电系统器件不确定性分析主要采用基于有限元模型的蒙特卡罗方法[5-6]。此方法的优点是数学模型简单、模拟精度高，缺点是过多的采样数需要耗费大量的计算资源。为提高蒙特卡罗仿真效率，计算模型采用集总参数模型[7]和降阶模型[8]，采样方法包括拉丁超立方采样[9-10]等。其他微机电系统器件不确定分析方法包括混沌多项式展开[11]、不确定性量化[12]和多项式拟合[13]等。人工神经网络计算速度快，相比于微机电系统器件的集总参数模型和降阶模型，仿真精度又具有明显优势。人工神经网络模型已经广泛应用于仿真微机电系统开关闭合电压[14-16]和S参数[17-18]、微机电系统谐振器谐振频率[19]和寄生模态[20]等。

现有的微机电系统器件不确定性分析方法存在仿真精度与效率无法兼得的缺点，仿真精度提高往往需要大量计算资源。为提高微机电系统麦克风不确定性分析方法的仿真精度和降低计算耗时，笔者建立基于人工神经网络的微机电系统电容麦克风灵敏度模型。通过随机采样和拉丁超立方采样蒙特卡罗模拟，研究振膜几何、材料参数的偏差对多晶硅圆形固支振膜微机电系统电容麦克风灵敏度不确定性影响。模型采用反向传播神经网络(Back Propagation Neural Network，BPNN)，输入包括麦克风振膜几何、材料参数，输出为机械灵敏度。

图1 微机电系统电容麦克风结构示意图

1 微机电系统电容麦克风设计

微机电系统电容麦克风由振膜、空气间隙、支撑区、固定背板和背板上的声孔等组成。笔者设计多晶硅圆形固支振膜麦克风，结构如图1所示。麦克风工作时，振膜与背板间施加直流偏置电压。在外部声波压力信号作用下振膜发生振动，造成振膜与背板之间电容变化，通过检测电路将其转化为电压信号输出。

图1中圆形振膜半径R，厚度h，空气缝隙高度g，背腔高度d，振膜弹性模量E，泊松比ν，几何及材料参数取值范围如表1所示。

表1 微机电系统电容麦克风振膜几何及材料参数取值范围

2 基于人工神经网络拉丁超立方蒙特卡罗模拟

2.1 人工神经网络模型

图2 微机电系统电容麦克风灵敏度人工神经网络模型结构

在Matlab软件环境中训练反向传播神经网络作为微机电系统电容麦克风灵敏度模型，模型输入为振膜半径、厚度和弹性模量，输出为灵敏度。采用单隐层5个神经元模型，网络结构简单、训练效率高，仿真精度测试结果满足设计要求。网络结构如图2所示。

振膜几何、材料参数取值范围如表1所示。为保证设计的人工神经网络模型仿真精度，通过Ansys软件共得到1 275组灵敏度数据，其中80%数据用于模型训练，20%数据用于模型验证及仿真测试。神经网络模型训练目标设为均方差小于1%，当模型仿真结果与训练数据之间均方差大于1%时，调整网络结构重新训练，直至神经网络仿真精度测试满足设计要求。与有限元方法计算结果相比，模型测试均方差为0.12%，完全满足设计要求。神经网络模型建立流程如图3所示。

2.2 拉丁超立方蒙特卡罗模拟

微机电系统电容麦克风工作过程涉及声学、力学、机械学和电子学等多学科，微尺寸三维结构及多物理场耦合导致灵敏度精确表达式无法得到，因此通过表达式求解灵敏度概率密度非常困难。蒙特卡罗模拟适用于计算过程复杂、难以得到研究对象精确表达式或者不存在解析解的情况，采用蒙特卡罗模拟分析微机电系统器件不确定性是当前研究热点。蒙特卡罗模拟根据输入参数的随机分布生成采样样本空间，通过海量计算模拟输出变量的概率密度。当采样规模足够大时，传统蒙特卡罗模拟具有很高精度；但是其缺点也非常明显，过于庞大的计算量导致模拟效率非常低下。

拉丁超立方蒙特卡罗模拟包括拉丁超立方采样和蒙特卡罗模拟两部分，是随机采样蒙特卡罗模拟的改进方法。拉丁超立方采样根据输入变量的概率密度函数进行分层采样，每个固定概率区间内只随机抽取一个采样点，有效解决随机采样中样本坍塌问题。与传统随机采样蒙特卡罗模拟相比，采用拉丁超立方采样的蒙特卡罗模拟输入空间覆盖率大，计算效率高，具有很好的鲁棒性。

图3 基于人工神经网络的的拉丁超立方蒙特卡罗模拟程序流程图

基于人工神经网路的拉丁超立方蒙特卡罗模拟程序流程如图3所示。模型包括两个子程序：人工神经网络模型建立及拉丁超立方蒙特卡罗模拟。蒙特卡罗模拟程序首先设置麦克风振膜半径、厚度和弹性模量概率密度参数，包括设计均值、偏差及分布类型；其次设置采样数，然后对输入变量空间进行拉丁超立方采样。采样点输入人工神经网络模型计算灵敏度，得到最终概率密度。如果蒙特卡罗模拟输出不收敛，则增大采样次数直至仿真收敛。

3 模拟结果及讨论

3.1 微机电系统电容麦克风灵敏度合格率

表2 微机电系统电容麦克风振膜参数设计值及偏差

笔者研究微机电系统电容麦克风，由制造工艺造成麦克风振膜参数偏差符合均匀分布，振膜设计值及偏差如表2所示。

设置采样数为100次，对振膜厚度、半径组成的二维空间进行随机采样和拉丁超立方采样，仿真结果归一化后采样点分布对比如图4(a)所示。采样数设为1 000次，对厚度一维变量进行随机采样和拉丁超立方采样，仿真结果归一化后概率密度对比如图4(b)所示。

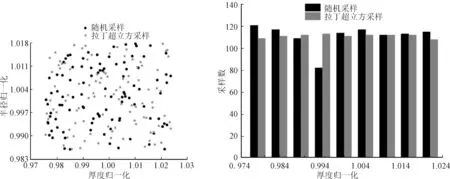
(a) 厚度、半径二维空间拉丁超立方采样点分布 (b) 厚度随机采样与拉丁超立方采样概率密度对比图4 随机采样和拉丁超立方采样点分布和概率密度对比

图4(a)中当采用随机采样时，采样点在某些区域过于集中，整个变量空间存在未采样区域，具有明显样本坍塌现象。相比于随机采样，拉丁超立方采样点在整个输入空间内分布更为均匀。图4(b)中随机采样的黑柱高度参差不齐，概率密度均匀性很差；拉丁超立方采样的灰色柱高度几乎完全一致，说明拉丁超立方采样在一维输入空间内分层均匀采样，具有良好的样本空间均匀性。

当振膜参数取设计值时，麦克风灵敏度为0.937 nm/Pa。文中设置灵敏度合格的偏差为±10%，即灵敏度在[0.84,1.03]范围内认为性能满足设计要求。图5所示随机采样和拉丁超立方采样蒙特卡罗模拟仿真麦克风灵敏度合格率随采样数变化曲线。

图5 蒙特卡罗模拟仿真灵敏度合格率随采样数变化曲线

如图5所示，随着采样率增加，蒙特卡罗模拟合格率逐渐收敛。当采样数为105时，两种采样方法蒙特卡罗模拟合格率均收敛到92.9%。当采样数大于9 000次时，随机采样模拟开始逐渐收敛于92.9%，计算耗时大约为2 min。当采样数为1 000时，拉丁超立方采样模拟收敛于92.9%，计算耗时仅为10 s。相比随机采样，拉丁超立方采样收敛需要采样点数仅为11%，计算耗时也大幅下降。总之，拉丁超立方采样蒙特卡罗模拟仿真麦克风灵敏度合格率计算速度快、精度高，是微机电系统电容麦克风灵敏度不确定性分析的优良方法。

3.2 微机电系统电容麦克风灵敏度概率密度

设置采样数为104，采用随机采样和拉丁超立方采样蒙特卡罗模拟麦克风灵敏度概率密度，计算结果对比如图6所示。由图6(a)可以看出，两种采样方法蒙特卡罗模拟结果相近。因此，基于人工神经网络的拉丁超立方蒙特卡罗模拟分析微机电系统电容麦克风灵敏度概率密度方法有效。采用正态分布拟合灵敏度仿真结果，均值μ=0.934，标准差δ=0.242。

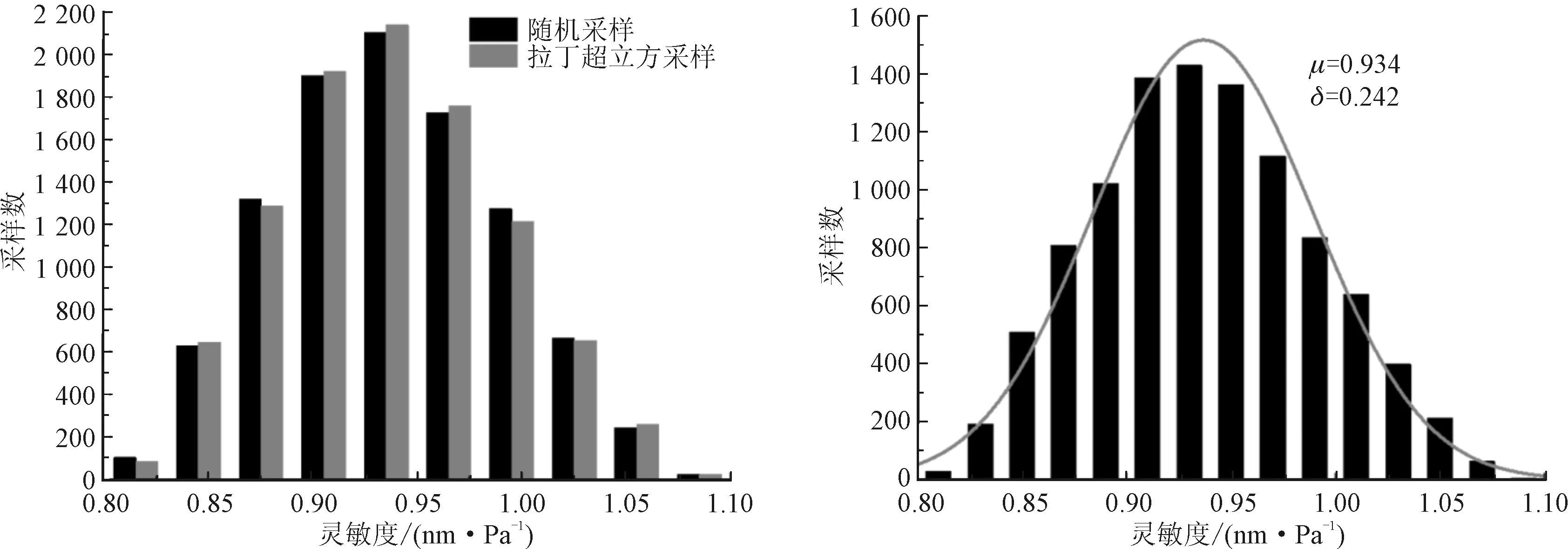
(a) 随机采样与拉丁超立方采样仿真灵敏度分布 (b) 正态分布拟合灵敏度分布仿真结果图6 随机采样和拉丁超立方采样蒙特卡罗模拟仿真灵敏度概率密度

改变振膜半径、厚度和弹性模量设计参数，利用拉丁超立方蒙特卡罗模拟仿真麦克风灵敏度分布箱线图如图7所示。由图可知，振膜几何、材料设计参数对麦克风灵敏度分布影响明显。图7(a)中随着振膜半径增大，灵敏度分布均值和标准差增大；图7(b)中随着振膜厚度增大，灵敏度分布均值和标准差减小；图7(c)中随着弹性模量增大，灵敏度分布均值减小，标准差几乎不变。由图示的变化趋势可以看出，振膜半径对灵敏度概率密度影响最为明显，厚度影响次之，弹性模量只影响分布均值，对标准差几乎没有影响。

图7 麦克风灵敏度概率密度随振膜几何、材料设计参数变化趋势

利用正态分布拟合图7所示灵敏度分布模拟结果，所得均值及标准差如表3所示。提高微机电系统麦克风灵敏度最为有效的方法是增大振膜半径，但是随着半径增大，由半径偏差造成灵敏度分布的标准差随之显著增大。如果制造工艺没有明显改善，则仅仅通过增大振膜半径设计值提高灵敏度会造成器件灵敏度合格率大幅下降。弹性模量只影响灵敏度分布均值，不影响标准差，所以降低弹性模量可以在保证合格率前提下有效提高麦克风灵敏度。但是弹性模量对灵敏度影响最小，仅适用于微调，大幅调整灵敏度仍需要改变振膜几何尺寸。

4 结束语

笔者研究多晶硅圆形固支振膜微机电系统电容麦克风灵敏度不确定性。现有的研究方法均存在仿真精度与效率无法兼得缺点，为提高仿真效率，笔者提出基于人工神经网络拉丁超立方蒙特卡罗模拟研究灵敏度不确定性。模型采用反向传播神经网络，输入参数包括振膜半径、厚度和弹性模量，输出的为灵敏度。通过Ansys软件仿真1 275组灵敏度数据训练神经网络。

采用蒙特卡罗模拟仿真灵敏度合格率，随机采样数大于9 000时仿真逐渐收敛于92.9%，计算耗时大约为2 min。相同仿真精度拉丁超立方采样仅需要1 000个采样点，计算耗时小于10 s，计算效率明显提高。当采样数为104时，二者仿真灵敏度概率密度差别也很小。因此，拉丁超立方蒙特卡罗模拟是分析微机电系统电容麦克风灵敏度不确定性的精确、高效方法。

表3 灵敏度分布均值和标准差随振膜参数设计值变化

笔者还研究振膜设计参数对麦克风灵敏度概率密度的影响。通过正态分布拟合蒙特卡罗模拟结果，得到灵敏度分布均值与标准差。计算结果表明，振膜半径对灵敏度分布影响最为明显，厚度影响次之，弹性模量只影响分布均值，不影响标准差。增大振膜半径，提高麦克风灵敏度的同时会降低灵敏度合格率。降低振膜弹性模量，在保证合格率前提下可以提高麦克风灵敏度，但是灵敏度提高幅度有限，仅适用于微调。