低相干高鲁棒性观测矩阵优化

赵 辉，张 乐，刘莹莉，张 静，张天骐

(1. 重庆邮电大学 通信与信息工程学院 重庆 400065；2.重庆邮电大学 信号与信息处理重庆市重点实验室 重庆 400065)

压缩感知(Compressed Sensing，CS)是2006年提出的一种新的采样技术，可以用低于奈奎斯特的采样速率采样信号，并且重构信号精度高[1]。压缩感知指出，在信号稀疏或在某个变换域是稀疏的前提下，首先利用稀疏基对信号进行稀疏表示，再使用观测矩阵将高维信号投影到低维空间得到观测值，最后从少量观测值中高概率地重构出原始信号[2]。压缩感知凭借其优越的性能被广泛应用于机器学习[3]、雷达[4]以及核磁共振[5]等领域。

压缩感知观测矩阵的作用是将测试信号投影成低维观测信号，而观测信号则直接影响了信号的精确重构[6]。当前对观测矩阵的研究大致可以分为两类：第1类是观测矩阵的构造。这类方法主要是从统计学角度讨论矩阵是否满足有限等距特性(Restricted Isometry Property，RIP)[7]或Spark性质，但求解这两个性质都是非确定性多项式(Nop-deterministic Polynomia,NP)难问题，在实际应用中并不适用；第2类是观测矩阵的优化。即构造优化模型时，先根据观测矩阵和稀疏字典的内积构造格拉姆矩阵，再对该矩阵进行优化处理，最后反解出优化后的观测矩阵。这类算法以降低观测矩阵和稀疏基的平均互相干性为目标，来保证稀疏信号的精确重构且算法复杂度较低。

文献[8]提出用平均互相干系数代替相干系数来表示观测矩阵与稀疏基的相关性，并通过线性收缩格拉姆矩阵中非对角元的绝对值大于固定阈值的方法减小相干性，实验效果较好。但该算法在运行过程中存在观测矩阵的降阶问题，且所采用的处理方法会产生绝对值较大的相关系数，影响算法的稳定性。文献[9]用等角紧框架建立的凸集合作为设计矩阵，使用梯度下降方法逼近凸集合求得观测矩阵，相比文献[8]，由于引入等角紧框架，算法更加稳定，但是梯度下降的步长需要根据经验确定，且步长因子的选择对算法的影响较大。文献[10]提出一种同时逼近等角紧框架和单位矩阵的模型，采用交替迭代算法求解，提高了系统的稳定性，但迭代次数较多。文献[11]在给定稀疏基的前提下，约束格拉姆矩阵的对角线为1，设计矩阵取单位矩阵，并求出优化模型的解析解，避免了梯度下降法迭代经验值步长的问题，提高了优化算法的性能，但该算法对字典的依赖性较强，且单位矩阵是一种严格约束条件，不适合做逼近目标。文献[12]提出先构造同时具有低相干性和紧致性的等角紧框架，再用感知矩阵逼近等角紧框架，最后用交替极小化方法求解，该算法虽然降低了平均相干性，但不适用于含噪信号，并且不能保证算法收敛于全局最优，系统的鲁棒性不强。

综上，目前的观测矩阵优化算法虽然能够降低观测矩阵和稀疏基之间的平均互相干性，但存在优化后观测矩阵普适性低和算法鲁棒性不足的问题。因此，针对以上问题，笔者提出一种新的观测矩阵优化算法。首先，通过观测矩阵和稀疏基的内积构造格拉姆矩阵，并收缩其非对角元，根据格拉姆矩阵构造符合要求的紧框架，将格拉姆矩阵同时逼近紧框架和单位矩阵，避免单位矩阵的严格约束问题，也降低了感知矩阵的平均互相干性；同时，考虑稀疏表示过程产生的误差，将稀疏表示误差作为正则项加入到优化模型中，提高感知矩阵的鲁棒性；最后，给出优化后观测矩阵的解析解，确保算法的收敛性。实验结果表明，与几种经典算法相比，笔者所提算法有效地降低了平均互相干性和重构误差，并提高了感知矩阵的鲁棒性。

1 基本理论

压缩感知理论指出：设N维信号x是在稀疏基Ψ下的K稀疏信号x=Ψs，其中‖s‖0=K,K≪N，CS使用M×N的观测矩阵Φ=(φ1,φ2,…,φM)对其进行采样，得到观测值y=(y1,y2,…,yM)，CS观测过程可表示为

y=Φx=ΦΨs=Xs。

(1)

由于M≪N，因此利用观测值y重构出信号x转换成求解l0范数优化问题：

(2)

求解式(2)是一个NP-hard问题，文献[1]证明l0范数可以放宽到l1范数，求得近似解为

(3)

观测矩阵的有限等距性和相关性为上述信号的重构问题提供了理论保证，相关定义如下。

定义1若观测矩阵Φ满足参数为(K,δK)的有限等距特性[7]，0<δK<1，则对所有K稀疏信号x，下式成立：

(1-δK)‖x‖2≤‖Φx‖≤(1+δK)‖x‖2。

(4)

定义2观测矩阵与稀疏基的相关系数以及平均互相干系数[8]的计算公式如下：

(5)

(6)

其中，Φi表示观测矩阵的第i列，Ψj表示稀疏基矩阵的第j列，gij代表格拉姆矩阵(G=ΨTΦTΦΨ)第i行j列的值，阈值γ∈[0,1)。相关系数反映观测矩阵和稀疏基之间列相关性的最大值，表示局部相关性；平均互相干系数反映绝对值大于或等于阈值的格拉姆矩阵非对角元绝对值的平均值，能够更加客观地评价观测矩阵的整体相干性。

由定义2可知，互相关系数表征观测矩阵和稀疏基的相似程度，理论上越小越好。文献[13]给出了互相关系数的最小值，即韦尔奇界限μWelch的表达式为

(7)

其中,M为测量值的个数，L为感知矩阵的列数。

框架是基在概念上的一种冗余扩展，目前常见的框架有Grassmannian框架、紧框架和等角紧框架。Grassmannian框架关注框架原子的相干性，紧框架关注框架的紧致性，等角紧框架兼具相干性和紧致性两种属性理应受到广泛应用。但已经证实，构造Grassmannian框架和等角紧框架相当困难，故文中构造不受维度限制且易实现的紧框架。下面给出紧框架的定义。

定义3对任意矩阵A∈RM×L是α-紧框架的3个充要条件是：

(1)矩阵A的M个非零奇异值均为α1/2。

(2)ATA的M个非零特征值均为α。

(3)α1/2*A的行向量是标准正交的。

2 观测矩阵优化算法

2.1 构造紧框架

(8)

2.2 观测矩阵优化模型

在优化观测矩阵过程中，为了保证重构质量，需要构造与稀疏基相干性较低的观测矩阵。一般情况，先构造格拉姆矩阵G=ΨTΦTΦΨ，再通过优化算法将格拉姆矩阵逼近于设计矩阵Gt来减小μav，具体模型如下：

(9)

在参考文献[11，14-15]中，设计矩阵皆取单位矩阵，但单位矩阵是一种严格约束条件，不适合做单一的逼近目标。文献[11]中将格拉姆矩阵对角线元素约束为1，仅考虑对角线元素，并没有减小感知矩阵的相干性。综上，笔者所提方法将设计矩阵取单位矩阵，通过约束格拉姆矩阵非对角线元素来降低感知矩阵的平均互相干性，并保证相关系数尽可能小，结合2.1节构造的紧框架，得到如下约束问题：

(10)

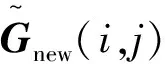
(11)

其中，α是拉格朗日乘子，也可称为格拉姆矩阵同时逼近两个设计矩阵的平衡参数。对式(11)化简，得

(12)

(13)

2.3 基于稀疏表示误差的观测矩阵优化模型

目前大多的观测矩阵优化算法假设原信号在给定字典下可以被绝对表示，但是在实际场景中，对于某些无法精确稀疏的信号存在稀疏表示误差[16]。鉴于此，为了构造鲁棒的观测矩阵，将稀疏表示误差作为正则项加入到式(13)中，提出的基于紧框架与稀疏表示误差的观测矩阵优化模型如下：

(14)

其中，E=X-ΨS，是稀疏表示误差；X=[x1,x2,…,xP]，是测试信号；S=[s1,s2,…,sP]，是测试信号对应的稀疏系数矩阵。式(14)是多变量优化问题，可采用交替优化求解Φ。求解算法如下。

基于紧框架和稀疏表示误差的观测矩阵优化算法：

输入：M×N维的高斯随机矩阵Φ1，N×L维的稀疏基Ψ，平衡参数α和β，韦尔奇界限μWelch，交替迭代次数n。

初始化：迭代次数k=1

fork=1:ndo

②对Gk先进行列归一化，再用下式进行收缩：

(15)

④根据式(14)更新观测矩阵Φk。

⑤Φk+1=Φk。

end for

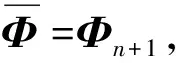
为了保证优化算法的收敛性，下面重点研究如何求解式(14)。先对矩阵Ge进行奇异值分解，即

Ge=VSVT=VS1/2(VS1/2)T=DDT，

(16)

其中，S∈RM×M,V∈RL×M,DT∈RM×L。式(14)可以化简为

(17)

令Q=[β1/2Ψ(1-β)1/2E],R=[β1/2DT0],Q∈RN×(L+P),R∈RM×(L+P)，优化问题可简化为

(18)

式(18)可用梯度法求解，如果没有选到合适的初始值，求解容易陷入局部最优解。为了解决这个问题并保证所提算法的收敛性，文中求解式(18)的解析解，得到如下定理。

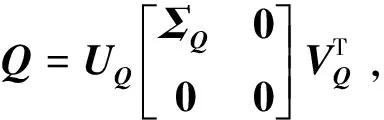
(19)

其中，RQ=RVQ=[R1R2],R1∈RM×rank(Q),Φ2∈RM×(N-rank(Q))。

证明：令ΦQ=ΦUQ=[Φ1Φ2],Φ1∈RM×rank(Q)，则

(20)

(21)

故化简后得到Φ1最小值为

(22)

则式(18)的解析解为

(23)

证毕。

3 仿真分析

为了验证文中算法的有效性，分别使用Elad优化矩阵[8]、Li优化矩阵[10]、Bai优化矩阵[12]和文中算法优化矩阵对比平均互相干系数、格拉姆矩阵非对角线元素直方图以及不同优化矩阵在正交匹配追踪 (Orthogonal Matching Pursuit, OMP) 算法下的重构误差。所有实验均在MATLAB R2014b环境下，硬件条件为Intel(R) Core(TM) i5-4590 CPU @3.30GHz，内存为7.87GB下完成。

3.1 矩阵性能分析

该部分主要对比几种优化矩阵的相关系数和平均互相干系数，以及相关系数的分布。选择初始观测矩阵为高斯分布的随机矩阵，固定稀疏基，对比随机矩阵、Elad优化矩阵、Li优化矩阵、Bai优化矩阵以及文中优化矩阵性能。其中Elad优化算法中收缩因子γ=0.95，阈值选t=0.4[8]；Bai优化算法中平衡参数w=0.4[12]；笔者提出的优化算法参数经多次实验后设置为：α=0.4,β=0.5，所有实验算法均迭代1 000次。

表1 低维不同优化矩阵相关性对比

注：表中黑体数字代表本行性能最优。

表2 高维不同优化矩阵相关性对比

注：表中黑体数字代表本行性能最优。

图1和图2是格拉姆矩阵列归一化后的非对角线元素绝对值的直方图，横轴代表非对角元绝对值的大小，纵轴代表非对角元的个数。从直方图可以看出，所提优化算法能大大减少感知矩阵中相关列的数目，在增加考虑稀疏表示误差后，直方图的值分布更为集中，并且减少了分布图的拖尾，说明了考虑稀疏表示误差后的优化矩阵更鲁棒。通过图1、图2的对比发现，在低维和高维观测矩阵中，所提算法优化效果均优于同类算法。

图1 低维优化矩阵直方图

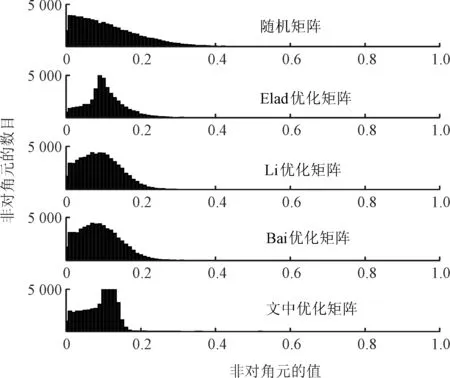
图2 高维优化矩阵直方图

图3 μav随迭代次数变化图

在Elad优化算法中，收缩因子γ值越小，算法收敛速度越快。文中对比所提算法与Elad算法验证所提优化算法收敛性，其中韦尔奇界限取μWelch={(120-25)/[25(120-1)]}1/2=0.18，Elad算法收缩因子γ分别取0.95，0.75，0.55。据实验结果分析，文中算法的收敛速度快于Elad算法的γ=0.75，略慢于γ=0.55，但收敛后的平均互相干系数μav是小于Elad算法的。由此可知，文中算法的收敛效果是优于Elad算法的。

3.2 重构性能分析

(22)

其中,N=1 000，表示稀疏信号的组数。由文献[17]知，当相对误差er大于一定门限值ρ∈(0,1)时，表示测试信号{sj}能够成功恢复，此处设置ρ=0.01。

本部分实验采用OMP重构算法验证各对比算法相对误差er随信号稀疏度K、观测矩阵行数M以及稀疏基列数L的变化曲线。稀疏度K对算法的重构性能有直接的影响。当观测次数已知时，稀疏度越高，相对误差越大。图4(a)中矩阵设置为：M=25，N=80，L=120，对于相同稀疏度，所提优化算法相对误差皆小于对比算法。图4(b)中参数设置为：K=4,N=80,L=120，当观测值M>25时，相对误差接近于零，信号能被精确重构。图4(c)中矩阵参数设置为：K=4,M=25,N=80，可以看到文中优化算法误差皆小于对比算法。

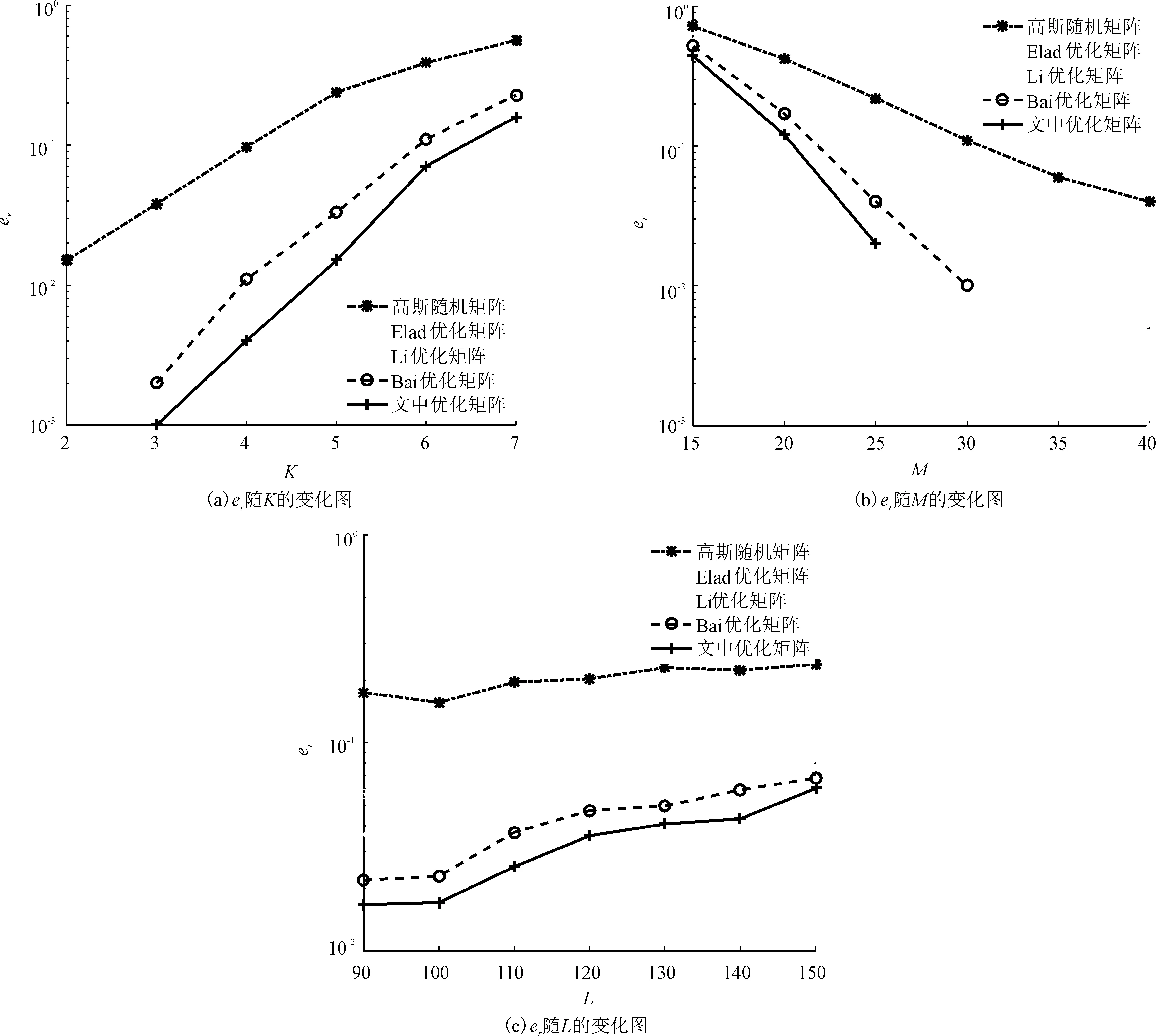
图4 不同优化算法下相对误差er随K,M,L的变化图

4 结束语

观测矩阵优化是提高压缩感知系统性能的关键。通过对观测矩阵优化问题进行深入研究，提出一种能降低观测矩阵和稀疏基矩阵间的相干性，同时能提高系统鲁棒性的观测矩阵优化算法。该算法在传统模型将格拉姆矩阵逼近单位矩阵的基础上，同时逼近构造的紧框架，以降低相干性，另外，考虑稀疏表示过程产生的误差，进一步优化模型，并求出优化算法的解析解。实验结果表明，采用所提优化算法，可以降低感知矩阵的平均互相干性，提高鲁棒性，重构误差也小于各对比算法。在实际应用中，所提观测矩阵优化算法确保了投影得到的低维观测值能尽可能多地保留原始信号的能量，进一步证实了所提算法的有效性。