一个不定方程的全部整数解

中国矿业大学环境与测绘学院 (邮编：221116)

江苏省海安双楼初级中学 薛锁英 (邮编：226671)

文[1]编入一道北欧数学奥林匹克竞赛题，求所有的整数组(x,y,z),满足三元三次不定方程x3+y3+z3-3xyz=2003；文[2-5]更进一步探讨了此方程的一般形式

x3+y3+z3-3xyz=d

①

现在，将方程①推广为四元三次的形式

w3+x3+y3+z3-3xyz-3wyz-3wxz-3wxy=d

②

其中d∈Z,d≠0；当w=0时，方程②退化为方程①；且得到

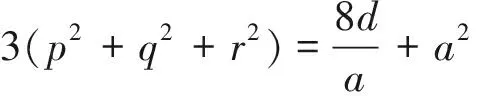
③

方程②满足w≤x≤y≤z的全部整数解包含于下列三个情形之中：

④

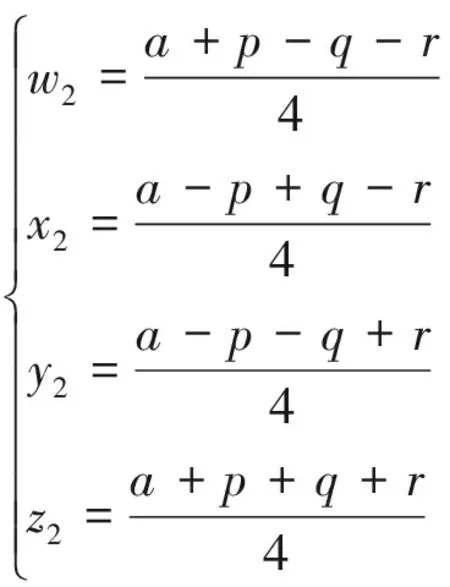
⑤

(3)若a为偶数，则w、x、y、z同时表为式④和式⑤.

证明方程②可变为

(w+x+y+z)(w2+x2+y2+z2-wx-wy-wz-xy-xz-yz)=d

⑥

令

w+x+y+z=a

⑦

|-w+x+y-z|=p

⑧

-w+x-y+z=q

⑨

-w-x+y+z=r

⑩

则a、p、q、r∈Z,0≤p；因w≤x≤y≤z,由式⑦、式⑧、式⑨及式⑩，易证0≤p≤q≤r；又因d≠0,由式⑥，知a≠0,a|d.

则式⑥变为

a[-a2+3(p2+q2+r2)]=8d

○11

因a3-a=(a-1)a(a+1)为三个连续整数的乘积，易知a3-a≡0(mod3),即

a3≡a(mod3)；由式○11，可得8d+a3=3a(p2+q2+r2)≡0(mod3)⟹

8d+a3≡-d+a3≡-d+a≡0(mod3)⟹a≡d(mod3).

联立式⑦、式⑧、式⑨及式⑩为线性方程组，并分为以下两种情形讨论：

○ⅰ若-w+x+y-z≥0,即-w+x+y-z=p时，线性方程组的解可表为式④.

○ⅱ若-w+x+y-z<0,即-w+x+y-z=-p时，线性方程组的解可表为式⑤.

注意到式④和式⑤均不是整系数，对于满足式③的任意一组(a,p,q,r)代入式④和式⑤中，可否确定地得到w、x、y、z的整数解，将分为以下两种情形做进一步讨论：

I. 若a为奇数

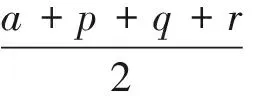
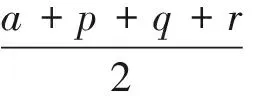
II.若a为偶数

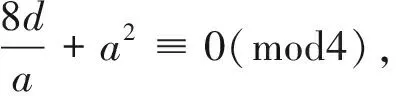
p2+q2+r2≡0(mod4),则p、q、r均为偶数，再分为以下两种情形讨论：

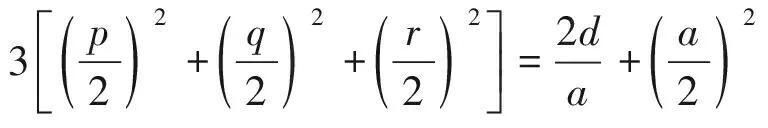
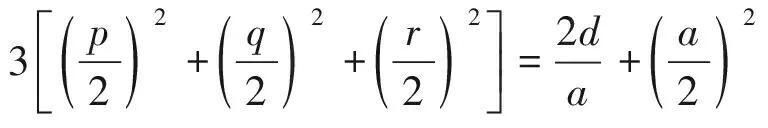
定理1成立.

例求方程w3+x3+y3+z3-3xyz-3wyz-3wxz-3wxy=20满足w≤x≤y≤z的全部整数解.

解由定理1，设a、p、q、r∈Z,0≤p≤q≤r,d=20,满足

○12

其中a|20,a≡20≡-1(mod3),则a=-1,2,-4,5,-10,20；又因

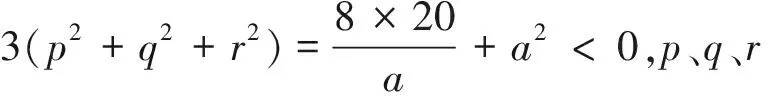
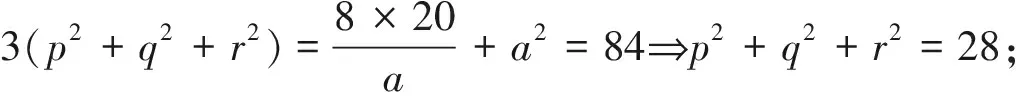
综上，仅需讨论a=5或20时的情形：

○ⅰ 当a=5时，由式○12得(a,p,q,r)=(5,1,3,3)；因a为奇数，且a+p+q+r=12≡0(mod4),则可将a、p、q、r的值代入式⑤，得(w,x,y,z)=(0,1,1,3).

○ⅱ 当a=20时，由式○12 得(a,p,q,r)=(20,0,6,10)或(20,6,6,8)；因a为偶数，则可将a,p,q,r的值分别代入式④和式⑤，得(w,x,y,z)=(1,4,6,9),(0,6,7,7)以及(3,3,4,10).

所求方程满足w≤x≤y≤z的全部整数解共有以上四组.

定理2 不定方程

w3+x3+y3+z3-3xyz-3wyz-3wxz-3wxy=0

○13

的全部整数解包含于下列两个情形之中：

①w+x+y+z=0；

②Dw=(α+β+γ)2，Dx=3α2+(β-γ)2，Dy=3β2+(γ-α)2，Dz=3γ2+(α-β)2；其中D,α、β、γ∈Z,D≠0.

证明：略.