错在哪里

北京丰台二中

甘志国 (邮编：100071)

题目(2017年高考浙江卷第15题)已知向量a、b满足|a|=1,|b|=2,则|a+b|+|a-b|的最小值是，最大值是.

解由题设，可得

由|a+b|≥0,|a-b|≥0知，可设

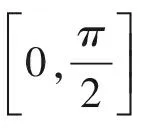
解答错了！错在哪里？

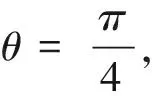
也就是说，用上述方法难以求出|a+b|+|a-b|的最小值.

下面再给出本题的五种解法.

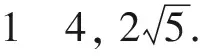
图1

A是半径为1的圆⊙O上的一个动点，构造两个全等的AOBD及ECOA,可得|a+b|+|a-b|=|AB|+|AC|.

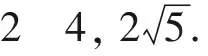
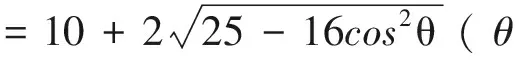
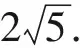
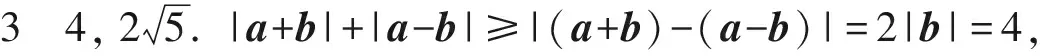
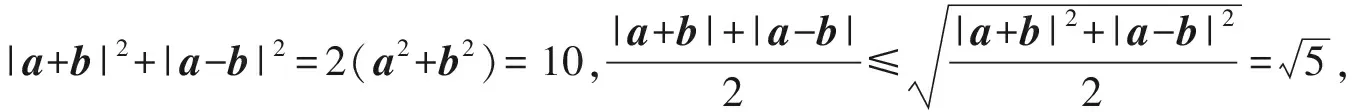
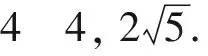
所以

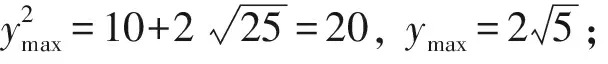
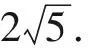
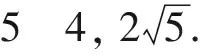
(|a+b|+|a-b|)2=[|(1+2cosθ,2sinθ)|+|(1-2cosθ,-2sinθ)|]2

再由cos2θ∈[0,1],可得答案.

类题已知向量a、b满足|a|=1,|b|=2,则2|a+b|+|a-b|的最小值是，最大值是.

=5(|a|2+|b|2)+6|a||b|cosθ+

(θ是向量a、b的夹角)

可设t=4cosθ(-4≤t≤4),得

令f′(t)=0,可得t=3.再由f(-4)=25,f(3)=50,f(4)=49,可得f(t)min=25,f(t)max=50,所以

(2|a+b|+|a-b|)min=5,

所以

接下来，同解法1.

(2|a+b|+|a-b|)2=[2|(1+2cosθ,2sinθ)|+|(1-2cosθ,-2sinθ)|]2

接下来，同解法2.

2合肥师范学院数学与统计学院

赵玉华(邮编：230601)

高等教育出版社《概率论与数理统计》(俗称盛骤版)第一章习题第24题如下：

有两箱同类的零件，第一箱装50只，其中10只一等品，第二箱30只，其中18只一等品.今从两箱中任意挑出一箱，然后从该箱中取零件两次，每次任取一只，作不放回抽样.求：

(1)第一次取到的零件是一等品的概率；

(2)在第一次取到的零件是一等品的条件下，第二次取到的也是一等品的概率.

配套的习题全解指南上给出的解答：

解答错了！错在哪里？

第(2)个问题，明显是分类讨论问题，而并不是用逆概公式的思路.这个问题中，事件A1和A2的含义各有两层：分别表示取第一箱和第二箱情况下的第一次取件和第二次取件.这样没有区分的事件A1和A2之间能有先后的顺序关系么？显然没有！取第一箱的事件A1不可能导致取第二箱的A2这个结果.而在解答中却把这两种意思揉和在了一起，首先对所求问题的表述就不对了；接着又不加以区分地运用条件概率定义和乘法原理，更是错上加错！所以只能按取到第一箱还是第二箱来分类，讨论对应的A1和A2.

正确解法如下：

P(A2|A1)=P(H)P(A2|A1H)

从中学生的视角，这个问题运用加法原理和乘法原理进行分类再分步，其实很容易解决.但是给大学生从高等数学的角度，特别是死板地套用贝叶斯(逆概)公式，反而做了错误分析.这种错误解法流行在许多高等数学教材和习题册中，需要引起重视.这也启发了我们的数学教学：引导学生在做题时对公式的产生背景和使用范围思考，而不是看到问题的表面相似就去机械地凑、套公式，这样必然会出现荒谬的结果.