盘活基本图形 提升两大能力

上海市岭南中学 (邮编：200435)

近年来，运用基本图形处理几何综合题已逐渐成为各类公开课教学展示的一道独特风景，并为广大师生所热捧．而随着2019年上海中考压轴题第25题的面世，本市必将掀起新一轮对几何基本图形研讨的热潮．

1 盘活基本图形，提升转化能力

所谓基本图形是指由常规几何图形(如线、角、多边形、圆等)与一些特殊线(如垂线、平行线、角平分线等)组成的具有特定规律性结论的基础图形，主要来源于教材中的定理和例习题，并为解决复杂的几何图形问题提供直接明了的思想方法或显性结论导向，是解题思路生成的一种重要源泉与突破口．

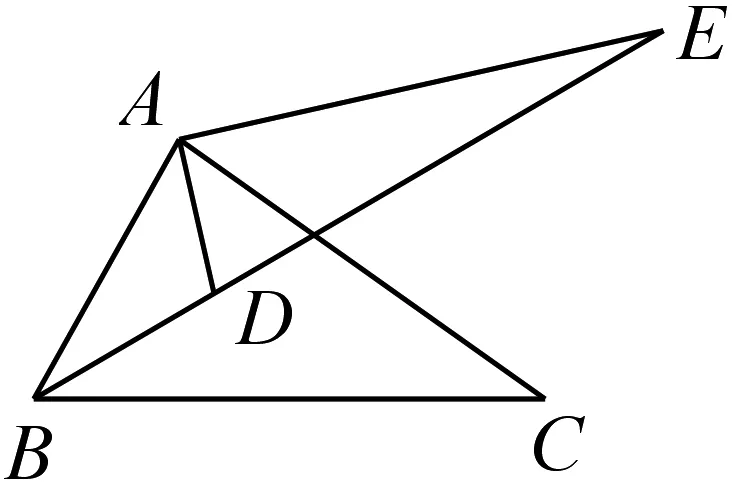
图1

图2

图3

例1(2019年上海中考第25题)如图1，在△ABC中，AD、BD分别平分∠BAC、∠ABC，过点A作AE⊥AD，交BD的延长线于点E．

(2)如图2，若AE=AB，且BD∶DE=2∶3，求∠ABC的余弦值；

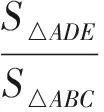
那么本压轴题又可挖掘出哪些基本图形？并为解题提供何种处理策略呢？

图4

图5

图6

图7

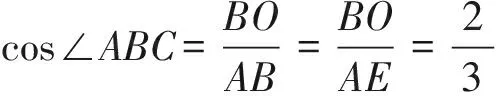
图8

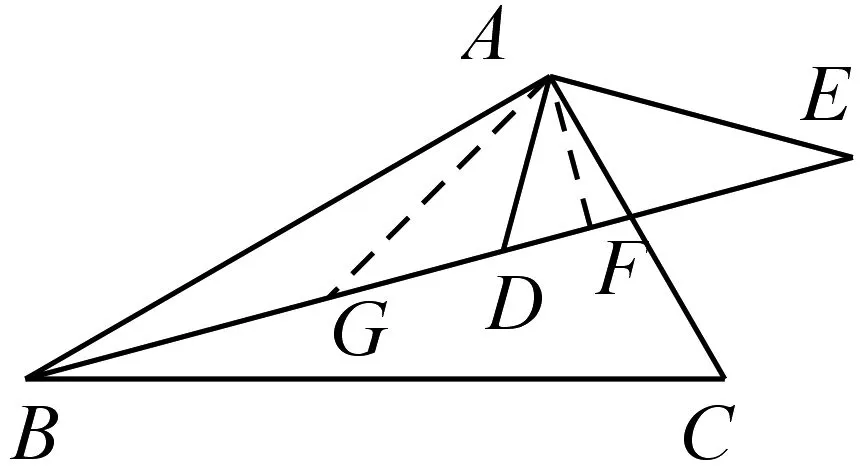
图9

由此可见，从综合题的复杂图形中巧妙地挖掘出基本图形往往能使解题思路有茅塞顿开之感和化难为易之妙，凸显了“化繁为简”与“化陌生为熟悉”的转化思想．当然，研究基本图形的积极意义不仅仅在于打开解题思路的又一扇窗，丰富转化策略，提高解题能力，更重要的是有利于其他学习能力的深化与发展．因为基本图形虽然来源于教材，但需从一定量同类问题处理中敏锐地观察出具有共性的经典图形，并挖掘出规律性的结论或具有较强启发性与广泛应用性的思想方法，而且在具体运用时又需从复杂的图形中精确地剖析出基本图形，自然对培养学生的观察力、归纳能力、分析能力和探究能力均大有裨益．

2 盘活基本图形，提升命题能力

其实，上海市2019年中考压轴题(即例1)来源于上教版七年级第二学期练习册第43页第4题(“探究与活动”)，原题如下：

图10

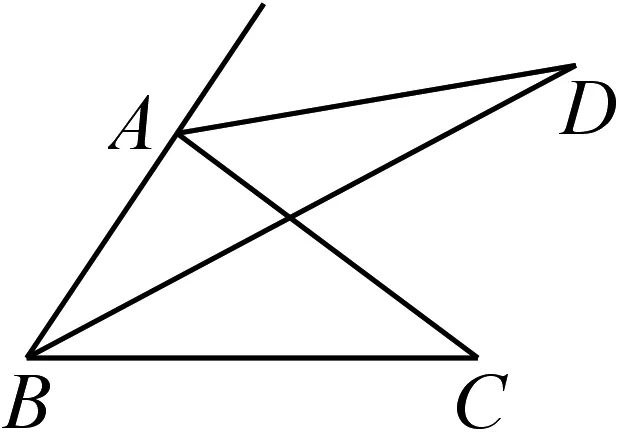
图11

(2)如图10，AD、BD分别是△ABC的两个外角的平分线，请你探究∠ADB与∠C之间有怎样的数量关系．

(3)如图11，AD、BD分别是△ABC的一个内角的平分线与一个外角的平分线，试探究∠ADB与∠C的数量关系．

对比例1(中考题)与例2(课本题)可知，中考题第(1)题就是由课本题第(1)题与第(3)题组合而成，即把图10与图3叠加，隐去边BA延长线部分，再把外角平分线改为内角平分线的垂线，便成了一道角度独特、导向新颖的中考压轴题的一部分；而中考题第(2)题既可以看成是基本图形5与图1 的组合，并从逆向角度进行重新设计与包装，也可看成是让图1的△ABC的形状“活”起来并特殊化为等腰三角形，再综合比例、锐角三角形函数等考点而得；进而继续让形状“活”起来的△ABC特殊化为直角三角形再加入相似三角形与解三角形的元素，便命制了把基本图形(图8)巧妙地隐含于求法中的第(3)题，也成就了一道“既来源于教材又高于教材”且“综合性强、能力要求高和梯度适中”的中考压轴题，走出了上海近几年压轴题命制的老路，给人以耳目一新之感．由此可见，从基本图形入手进行适当变形与考点综合，也是命题的一种重要策略和提高命题能力的有效途径．

另外，除了上述重组方法外，把基本图形拆分也是编制考题一个重要策略，如下面的2019年上海市中考第18题．

例3 在△ABC与△A1B1C1中，∠C=∠C1=90°，AC=A1C1=3，BC=4，B1C1=2，点D、D1分别在AB、A1B1上，且△ACD≌△C1A1D1，则AD的长是．

图12

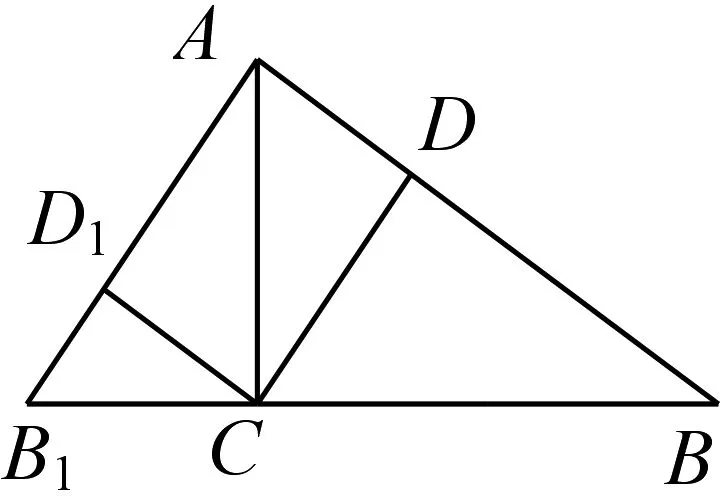
图13

当然，对基本图形进行重构的方法除了重组与拆分外，还有让部分元素动起来等化静为动的技巧，甚至把封闭图形设置为开放图形、把封闭问题设置为开放问题都不失为重构的有效策略．

3 两点思考

(1)基本图形教学要立足于“挖”

首先，要借助定义定理教学挖掘基本图形．在几何定义和定理中不乏一些典型的基本图形，如由等腰三角形所联想的“三线合一图”、平行线分线段成比例定理所衍生的“X型图与A型图”和射影定理所隐含的“母子相似图(即图13中的∠BAC为直角)”等．从这些深深刻在学生脑海里的图形入手开展基本图形教学，自然有一份潜在的亲切感，容易引起学生的共鸣，不知不觉中强化了对基本图形的认识．

其次，要依赖思想方法的生成挖掘基本图形．在一些问题解决的思想方法中往往含有大量基本图形的典型素材，如由中心对称图形所引发的“三角形中线倍长图”、证明三条线段和差关系的“截长补短图”和解直角三角形中的“双仰角测量图(即图8)”等．深入挖掘此类基本图形可以极大地丰富处理问题的转化策略，提升解决问题的类比迁移能力．

最后，要善于从复杂图形中挖掘基本图形．加强对基本图形的直观感受训练，注重由条件到基本图形的迁移联想，强化“去支存主(隐去干扰线凸显主脉线)”的剖图技巧，进而提高学生从综合图形中厘析基本图形的意识与能力．

当然，关于基本图形的教学切忌走“教师归纳学生硬套”的量化强塞之路，而要创设必要的观察情境(即把同类问题适当归类)，引导学生感悟共性、大胆猜想并发现规律，体验生成过程，使基本图形成为学生自主探究的成果，并深挖基本图形构成要素，建立由条件到基本图形的联想通道，使基本图形真正成为学生处理问题的转化策略与致胜法宝．

(2)由基本图形切入命题要突出“变”

命制几何题是一个创新的过程，是一个把基本图形不断加工的重构过程，故而成败的关键就在于“求变”．着手于图形与图形重组、知识与知识综合力求“量变”，立足于平移、翻折和旋转力求“位变”，侧重于化静为动(如点、线动起来)、化一般为特殊(如四边形——平行四边形——菱形——正方形)与化少维为多维(如三角形到四边形)力求“形变(即形状变化)”， 当然也可从语言描述、逆向切入和数形结合等角度“求变”．但不管如何“求变”，只要注意表述的规范、梯度的把握与能力的导向，就一定能编制出创新味浓厚的好题．

总之，对基本图形的研究要力求水到渠成，以发展能力为宗旨，切不可模型化操作，教学生死套，否则，只会加重学生负担，适得其反也！