导函数为指（对）数、三角函数等形式的分类讨论

南京市教学研究室 龙艳文

导数这一章节的重点问题为利用导数研究函数的单调性和极（最）值问题.导函数为指（对）数、三角函数等形式，且无法直接求出零点和单调性时，需要对导函数进行二次求导，从而需要对二次求导的导函数进行分类讨论.我们通过对一组问题的归类研究，从各种复杂的分类中找出共同规律，提炼出有章可循的分类途径和方法，从而构建导函数为指（对）数、三角函数等形式的分类讨论的解题思维模式结构图.

一、解题思维模式形成

例1设函数f（x）=ex-1-x-ax2.若x≥0时，f（x）≥0，求a的取值范围.

解：由f（x）=ex-1-x-ax2，

得f（0）=0，f′（x）=ex-1-2ax.

令G（x）=f′（x）=ex-1-2ax，

则G（0）=0，G′（x）=ex-2a.

优先判断f（0）=0，求导f（x），令G（x）=ex-1-2ax，要判断G（x）的零点，需判断G（x）特殊点的正负和单调性

令H（x）=G′（x）=ex-2a，

则H（0）=1-2a，H（x）在（0，+∞）上单调递增.

求导G（x），令H（x）=ex-2a，要判断H（x）的零点，需判断H（x）特殊点的正负和单调性

① 当1-2a≥0，即a≤时，

所以x∈（0，+∞）时，H（x）＞0，即G′（x）＞0，

所以函数G（x）在（0，+∞）上单调递增.

因为x∈（0，+∞）时，G（x）＞G（0）=0，即f′（x）＞0，

所以函数f（x）在（0，+∞）上单调递增.

当x∈[0，+∞）时，f（x）≥f（0）=0，

所以当a≤时，满足条件.

由H（0）≥0和H（x）递增，结合H（x）图象，判断G（x）递增.再由G（0）=0，判断G（x）在（0，+∞）上恒正

② 当1-2a＜0，即a＞时，

令H（x）=0，得x=ln2a.

所以当x∈（0，ln2a）时，H（x）＜0，即G′（x）＜0，

所以函数G（x）在（0，ln2a）上单调递减.

因为x∈（0，ln2a）时，G（x）＜G（0）=0，即f′（x）＜0，

所以函数f（x）在（0，ln2a）上单调递减，

当x∈（0，ln2a）时，f（x）＜f（0）=0，

所以当a时，不满足条件.

由H（0）＜0和H（x）递增，结合H（x）图象，判断G（x）在（0，ln2a）上单调减.再由G（0）=0，判断G（x）在（0，ln2a）上恒负，故f（x）在（0，ln2a）上单调递减.

综上，a的取值范围（-∞，].

二、解题思维模式构建

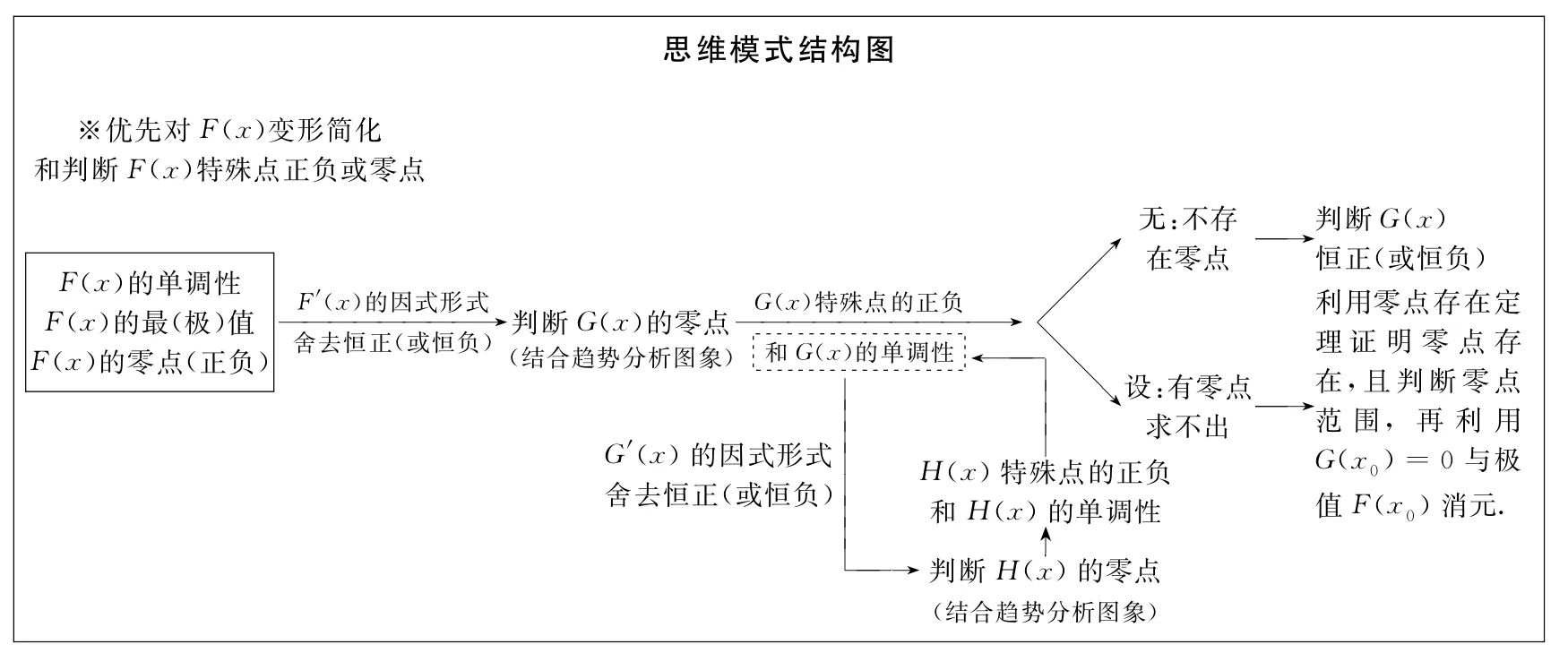
三、解题思维模式应用

例2（2019全国Ⅰ卷文科）已知函数f（x）=2sinx-xcosx-x.若x∈[0，π]时，f（x）≥ax，求a的取值范围.

解：设F（x）=f（x）-ax=2sinx-xcosx-x-ax.

由x∈[0，π]时f（x）≥ax恒成立，即F（x）=2sinx

xcosx-x-ax≥0恒成立，

则F′（x）=cosx+xsinx-1-a，

且F（0）=0，F（π）=-aπ.

令G（x）=F′（x）=cosx+xsinx-1-a，

则G（0）=-a，G（π）=-2-a，且G′（x）=xcosx.

优先判断F（0）=0，求导F（x），令G（x）=cosx+xsinx-1-a，要判断G（x）的零点，需判断G（x）特殊点的正负和单调性

调递增；

调递减；

① 当a≤-2时，G（π）≥0.

当x∈（0，π）时，G（x）＞0，则F（x）在（0，π）上单调

递增.

所以F（x）min=F（0）=0.

所以当a≤-2时，F（x）≥0对x∈[0，π]恒成立.由G（π）≥0和G（x）单调性，判断G（x）无零点，从而G（x）恒正

②当-2＜a≤0时，

G（0）=-a≥0，G（π）=-2-a＜0，

存在x0∈（，π），使得G（x0）=0.

当x∈（0，x0）时，G（x）＞0，所以F（x）在（0，x0）上

单调递增；

当x∈（x0，π）时，G（x）＜0，所以F（x）在（x0，π）上

单调递减.

因为F（0）=0，所以F（π）=-aπ≥0，则a≤0.

所以当-2＜a≤0时，F（x）≥0对x∈[0，π]恒成立.

由G（0）≥0，G（π）＜0和G（x）单调性，判断G（x）存在零点，从而判断零点两侧G（x）的正负

当x∈（0，x1）时，G（x）＜0，所以F（x）在（0，x1）上单调递减.

因为F（0）=0，所以x∈（0，x1）时，F（x）＜0，

由G（0）＜0，和G（x）单调性，判断G（x）存在零点，从而判断零点两侧G（x）的正负

当x∈（0，π）时，G（x）≤0，则F（x）在（0，π）上单调递减.

因为F（0）=0，所以x∈（0，π）时，F（x）＜0.

综上，a≤0.

注：利用F（π）=-aπ≥0，得a≤0，可减少分类讨论.

四、解题思维模式练习

1.已知函数f（x）=-2xlnx+x2-2ax+2a-1.若x≥1时，f（x）≥0，求a的取值范围.

2.设函数f（x）=xex-asinxcosx（a∈R）.

（2）是否存在实数a，使得函数f（x）在区间）上有两个零点？若存在，求出a的取值范围；若不存在，请说明理由.

3.（2019全国Ⅱ卷理科）已知函数f（x）=ex-ax2.

（1）若a=1，证明：当x≥0时，f（x）≥1；

（2）若f（x）在（0，+∞）只有一个零点，求a.

4.已知函数f（x）=cosx+ax2-1，a∈R.若对于任意的实数x，f（x）≥0恒成立，求实数a的取值范围.

1.a≤0.2.（1）a的取值范围是（-∞，1]；（2）不存在实数a，使得函数f（x）在区间]上有两个零点.3.（1）略；（2）