基于岭回归的工资预测模型

(西安财经大学统计学院 陕西 西安 710100)

一、引言

工资是劳动者劳动收入的主要组成部分，是GDP核算的重要依据之一，它可以用来衡量和反应收入、分配与劳动力发展水平。有效进行工资预测，为劳动经济决策提供依据，对研究劳动经济发展趋势有重要意义。

随着线性回归模型的应用越来越广泛，已经有研究开始注意到线性回归模型的稳定性这个问题。特别是当模型中的变量是线性相关时，它违背了线性回归模型的基本假设。如何修改这些假设以满足基本假设成为解决多重共线性问题的关键。通用解会丢失变量提供的有用信息，降低模型的解释度，从而影响模型的应用价值。不同岭回归方法，该方法是给保持无偏的，有用的信息模型变量的估计，具有较小的平均平方误差获得的模型参数，从而稳定模型参数以改善模型的解释这个问题的能力。岭回归是解决数据共线性这种病态特征的有效方法，是最小二乘法的改进，估计的参数能真正反映自变量与因变量之间的客观联系，在一些领域获得了成功应用。

二、工资预测的岭回归模型

(一)变量的抽象过程

随着我国综合实力日益增强，我国居民的工资水平也在不断提高，影响工资的因素有很多，需要多个方面进行说明。本文以工资为模型的内生变量Y，选取了受教育年限X1、居住区域X2、性别X3、工作经验X4、是否为工会成员X5、每小时工资X6、年龄X7、种族X8、职业类型X9、工作部门X10为模型的外生变量。

(二)模型的建立

根据已经选取的10个外生变量对模型的内生变量工资进行回归，来建立线性回归模型

Y=β0+β1X1+β2X2+…+β10X10+ε

(1)

(三)模型的诊断

对模型(1)进行进一步分析。首先对已有数据进行标准化，去除量纲对回归方程所带来的影响。用SPSS软件运行并输出结果。其中第一列为岭参数k，软件默认值k从0～1，步长为0.05，共有21个k值。第二列是决定系数R2，第3～12列是标准化岭回归系数，其中第一行k=0的数值就是普通最小二乘估计的标准化回归系数。

通过观察图1、图2，发现变量X6、变量X7、变量X9、变量X10是共线的且比较稳定，因此我们决定剔除这三个变量，用Y与其余自变量做岭回归。

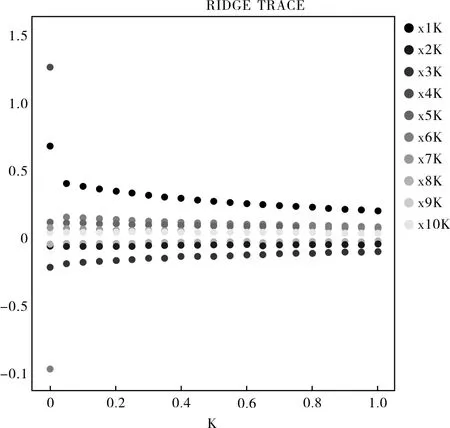
图1 岭迹图

图2 相关系数与岭回归参数的关系

(四)模型的改进

通过上面的分析，我们把岭参数步长改为0.02，范围减小到0.2。再用SPSS软件对剔除后的变量做岭回归。

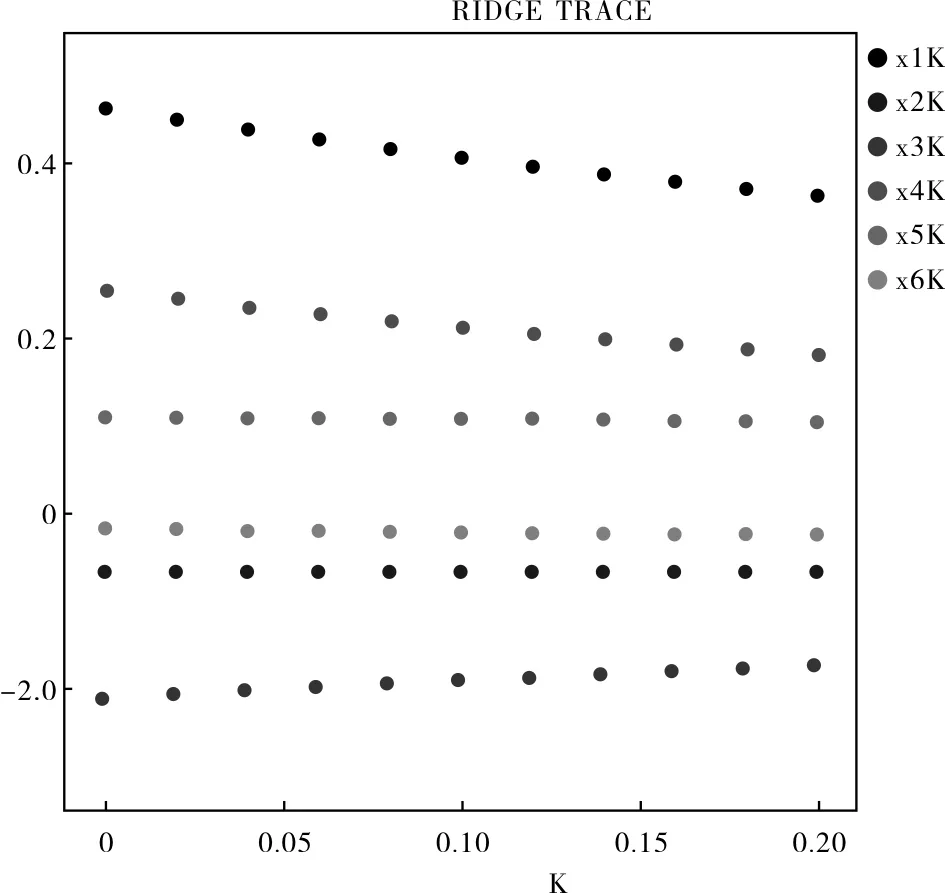
图3 岭迹图

图4 相关系数与岭回归参数的关系

由SPSS结果发现R2在k=0.04到k=0.06之间发生比较大的变动，从0.269 11变到0.268 35，因而可以选取岭参数k=0.05。然后定k=0.05，重新做岭回归。

计算结果如表1所示。

表1 Ridge Regression with k=0.05

表2 ANOVA table

表3 Variables in the Equation

得到Y对X1，X2，X3，X4，X5，X8的标准化岭回归方程为

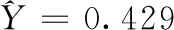
未标准化的岭回归方程为

三、结论

本文通过对因变量工资水平与十一个自变量的相关系数矩阵，用SPSS软件画出岭迹图，通过分析岭迹图剔除影响较小的几个因素，对剔除变量后的数据重新做岭回归，并改变步长，从而确定k值，然后用软件做出模型结果。

由于在实际社会经济中的数据具有很强的相关性，在回归过程中时很可能出现多重共线性问题，通过共线性分析得到预测变量具有很强的共线性。因此，本文采用岭估计方法消除了预测变量间的共线性，得到了更加稳定的回归系数估计值，根据建立的岭回归预测模型可以预测出新的样本的工资水平，且模型通过了验证。