VaR模型在股票收益率风险度量中的应用
——以中国平安为例
(天津财经大学 天津 300222)
一、引言
随着经济全球化和金融市场一体化进程的推进,全球金融市场也呈现出前所未有的波动性,金融风险管理也越发重要,风险如果管理不好,就有可能造成巨大的损失。比如中海油从事石油期权,亏损几十亿元,如果情况进一步恶化还有可能会引发经济危机,给国民经济带来沉重的打击,因此金融市场的风险管理尤为关键。而股票市场作为金融市场的重要组成部分,随着其制度不断的完善,越来越多的人进入股市,股票市场的波动,股价的波动也牵动着人们的心,因此,股票市场的风险管理有利于国家经济的稳定发展。
而风险度量则是风险管理中重要的一环,能否对风险进行精确度量直接决定了风险管理的有效性,随着金融市场交易规模的不断扩大,动态性和复杂性不断增加,金融市场风险的测量技术也变得越来越综合,其中VaR模型是目前金融市场风险测量的主流方法之一。因此本文将VaR模型应用于股票的收益率的风险度量中,采用常用的三种方法进行实证,判断哪种方法更具有精确性,更适用于股票市场。
二、理论模型概述
(一)VaR的定义
VaR的英文全称为Value at Risk,基本涵义是“处于风险中的价值”,是指市场正常波动下,在特定持有期和置信水平下,某一金融资产或证劵组合的最大可能损失。
在统计上可以表示为P{损失额>M}<α,其中置信水平为1-α,M即为VaR
(二)VaR的计算方法
总的来说,VaR的计算方法分为参数法和非参数法两大类,下面对三种常用的计算方法进行介绍
1.历史模拟法
历史模拟法是所有计算方法中最简单和直观的方法,是一种非参数法。它的核心在于根据市场因子(通常是收益率的均值,方差等)的历史样本变化模拟证券组合未来的损益,然后根据模拟出的损益分布进行计算。传统的历史模拟法本质上是利用直方图进行分析的一种非参数密度估计。
2.蒙特卡洛模拟法
蒙特卡洛模拟法也是一种非参数法,与历史模拟法不同的是,这种方法是通过建立随机过程来模拟未来市场因子变化,重复模拟随机过程,模拟出市场因子各种的可能,并在此基础上构造损益分布,根据分位数就可以求出VaR值。最常用的模拟模型是随机游走模型和几何布朗运动。
3.GARCH(1,1)模型
大部分的金融时间序列数据具有波动集群效应,即条件方差并不是常数。在收益率的波动方面,1982年,以Engle为代表的研究者,创造性地提出了ARCH()模型,并将该模型用于分析在英国的通胀指数的波动聚集性。紧接着在1986年,Bollerslev将基础的波动率模型-ARCH模型进行了改进,提出了广义的ARCH模型,即GARCH()模型,大量研究表明,GARCH(1,1)模型就能够较好地拟合金融数据的波动集聚性,因此在实践中通常采用GARCH(1,1)模型来进行计算。
(三)VaR的回测
回测的目的是对所构建的VaR模型进行检验,判断所建立的模型是否有效,能否有效地应用在未来的数据中。最常使用的一种方法是Kupiec在1995年提出的一种似然比检验方法。
检验统计量为
在零假设成立的条件下,考察次数M足够大时,LR统计量渐进服从自由度为1的卡方分布,则在95%的置信水平下,如果LR统计量的值小于3.841,则不能拒绝原假设,认为模型是可以接受的。
三、实证分析
(一)数据来源与定义
1.数据来源
数据来自网易财经网站,是中国平安的股票,股票代码为601318。
采用2016年1月4日~2019年4月23日的数据进行分析,收益率采用对数收益率,以2016年1月5日~2018年4月23日的收益率来测算VaR,共560个数据,以2018年4月24日~2019年4月23日的收益率进行回测,共243个数据,计算持有期为1天,置信水平为95%的VaR。
2.选股原因
上证指数对大盘有很重要的影响作用,而中国平安是上证指数的权重股,同时是上证50、上证180成分股,对上证指数影响较大,因此比较有研究价值。时间从2016年开始是因为2015年发生了很严重的股灾,属于比较极端的现象。此外,历史模拟法计算的精确性也有赖于较大的数据量,结合参考文献,认为当样本达到500以上时即为大样本,因此本文采用560个样本进行计算
(二)数据描述与相关检验
1.收益率的趋势描述

图1 中国平安股票的收益率
由图1可知,对数收益率表现出了明显的波动集群性,即一个较小的波动跟随着一个较小的波动,而一个较大的波动后面往往是一个较大的波动。
2.收益率基本特征描述
根据已有的数据,利用软件对收益率的均值、方差、偏度、峰度四个统计量进行计算,其中均值为0.001 154,从数值上看,与0没有明显的差别。方差为0.000 240 224 1,收益率的偏度为0.104 483 8,说明数据的偏离程度比较小,而峰度为2.457 152,说明收益率数据具有尖峰厚尾的特征。
3.收益率的正态性检验
Shapiro-Wilk检验的W值为0.947 36,对应的p值为3.228e-13,远远小于0.05,因此,在5%的显著性水平下,拒绝原假设,即我们有理由相信,收益率数据是不服从正态分布的。不过这一结论也不意外,由数字特征我们就可以看出数据具有尖峰厚尾特征,不符合正态分布的特征,此外,大部分的金融数据都不服从正态分布。
(三)模型建立
我们采用常用的3种方法进行计算,并对回测结果进行一个对比。
1.历史模拟法
已知样本容量为560,先对这560个样本收益率进行排序,则95%置信水平下的VaR对应的顺序统计量为560×5%=28,及第28个对数收益率即为VaR,得到VaR1=-0.024 678 92。
2.蒙特卡洛模拟法
在本次实证中,以2018年4月23日作为t,4月24日作为T(因为计算的是持有期为1天的风险价值),将这一天划分为20个阶段,用布朗运动这个随机过程来模拟这20个阶段的价格变动趋势,重复进行5000次模拟,得到5000个模拟价格,再根据价格计算出收益率,对收益率进行排序,最终计算得到风险价值VaR2=-0.025 411 36。
3.GARCH(1,1)模型
首先对模型进行相关检验,判断数据是否适用于GARCH模型。检验包括三部分,分别为平稳性检验,白噪声检验以及数据的ARCH效应检验,检验得到的结果如下。
平稳性检验:adf检验的p值小于0.05,拒绝原假设,即认为收益率是平稳的。
白噪声检验:Box检验,p值为0.481 3,因此不能拒绝原假设,认为收益率数据是白噪声。
ARCH效应检验:McLeod.Li检验的表明,滞后阶的p值从2阶之后就落在5%的置信区间内,表明数据具有比较强的ARCH效应。
根据以上检验的结果可知,对于该数据,适合建立GARCH模型来拟合条件方差,而对于均值函数,则用一个随机扰动项加一个常数即可。
得到了三种分布下方差的拟合方程及各自的VaR如下。
正态分布得到的VaR3=-0.031 630 96
t分布得到的VaR4=-0.028 831 49
广义误差分布得到的VaR5=-0.031 750 93
4.模型回测
不同方法的回测结果。
由软件计算得到历史模拟法,蒙特卡洛模拟法、GARCH(1,1)正态分布、GARCH(1,1)t分布、以及GARCH(1,1)广义误差分布所对应的失败次数分别为20、19、11、14、12,LR统计量的值分别为4.506 14、3.495 473、0.118 173 6、0.283 253 9、0.001 956 965,由理论知识可知,当统计量的值大于3.81时,有理由拒绝原假设。因此在五种情况下,只有历史模拟法拒绝原假设,即认为模型的设定是不合理的,其余四种情况均不能拒绝原假设。因此认为蒙特卡洛模拟法以及GARCH模型构建的模型是合理的。
广义误差分布下GARCH模型的回测结果如图2所示。
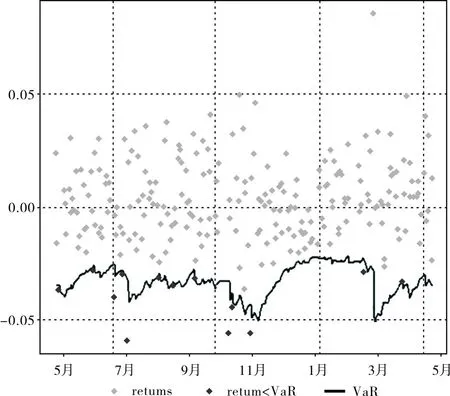
图2 广义误差分布下GARCH()模型的回测图
在前面的回测中,给出了三种分布下GARCH模型拟合的VaR值,实际上随着时间的推移,GARCH模型涉及的变量,如均值和方差,会随着回测数据的更新而发生变化,GARCH模型会自动计算出每一天的VaR。图2展示了在广义误差分布下每一天的VaR和每一天的真实值比较的结果,深灰色点表示真实值小于VaR,即损失超过正常水平的次数,共有13次,与理论的12次没有明显的差距,不能拒绝我们设定的模型。此外,GARCH模型的这种回测方法更具有代表性和说服力,因为它是采用每一天计算的VaR和每一天的真实值进行比较,这样的对比更加具有针对性。
(四)实证结论
第一,历史模拟法是五种情况下唯一一个拒绝原假设的,即认为所算的VaR不符合真实的情况。究其原因,可能是因为2018年股市整体处于比较低迷的状态,而历史模拟法的假设就是未来与过去的变化要完全一致,这一假设本来就不是很符合实际情况,因此在市场出现较大的波动时,历史模拟法往往是不够准确的。
第二,蒙特卡洛模拟法虽然没有拒绝原假设,但统计量的值处于比较边缘的位置,其失败次数为19次,与理论预期的243×5%=12.15相差较远。可见,用随机模拟可以消除一些误差,但仍然不够精确。
第三,GARCH模型的三种分布拟合效果都不错,即使假设“新息”服从正态分布,仍能较好的模拟出金融数据“尖峰厚尾”的特征,在三种分布中,广义误差模型表现最优。
四、结论与建议
第一,历史模拟法是所有计算方法中最简单直观的一个,因此也受到企业管理者的青睐。例如,我国国有银行就采用这种方法,但其“未来的变化与过去完全一致”的假设显然不太符合瞬息万变的股票市场,其计算结果往往也是有偏差的,因此在波动幅度较大的年份,不建议使用这种方法。
第二,蒙特卡洛模拟法利用随机过程来拟合本身就具有随机性的收益率,是一种很有效的方法,但是对于上百种资产组合的计算,可能就对计算机的性能有一定的要求,而且比较耗费时间。
第三,GARCH模型产生的原因就是为了更好地展现金融数据所具有的波动集聚性,因此它能够较为精确地计算出数据的条件方差,进而度量数据的风险。此外,正如实证分析部分所展示的那样,GARCH模型可以算出连续多天的VaR,其回测的准确性要高于其他的模型。
结合上面三种方法的对比,笔者认为,在正常年份,即股票市场不存在大的波动或者突发情况时,可以采用历史模拟法作为风险度量的方法,而波动较大时显然不适宜采用历史模拟法。蒙特卡洛模拟法适用于比较小型的公司,资产组合的数量比较少,计算的效率也不会很低。而GARCH模型是三种模型之中最优的那个,尤其是广义误差分布下的GARCH模型,可以在实践中优先考虑。

