断开式转向系统应用于不同车型的快速调整设计方法

孟红芹

(中国公路车辆机械有限公司， 北京 100160)

1 断开式转向系统调整困难的原因

在独立悬架的应用过程中，为了使双侧轮胎上下跳时互不影响，需要将转向系统做成断开式[1-2]。断开式转向系统有多种形式，本文为三段式，主要由中间横拉杆和左、右转向横拉杆组成。该种布置形式可实现车辆的低地板，宽通道，短前悬，门可开在前轴前端。该结构适用于多种车型。

车辆的内、外转角对应关系对轮胎的磨损影响很大。理论的内、外转角应满足式(1)所示的阿克曼转向几何关系[3]，这一理论为转向系统的设计和调整提供了依据。

cotθo-cotθi=K/L

(1)

式中：θo、θi分别是车轮外、内转角；K是左右主销中心线延长线与地面的交点间距；L为车辆轴距。

当车型改变时，K和L可能会随之变化，导致原有的内外转角关系无法满足新车型需求，因此需要调整转向系统。

断开式转向系统杆件多，结构复杂[4-6]，调整难度大。设计断开式转向系统时，常采用的方法有图解法、网络法，同时结合Matlab和ADMAS虚拟样机进行分析[7-10]，能够较为精准地进行设计，但是耗时长，一般适用于转向系统初始设计阶段。对于已成型的转向系统产品，其杆件和节臂多为开模件，重新开发制造成本高、生产周期长。在市场应用中，要求动作快、时间短、成本低，因此需要最大限度借用现有产品，结合常用软件，快速调整参数，达到设定目标。

为使同一断开式转向系统快速、低成本地满足不同车型需求，本文提供一种快速调整转向系统的设计方法。

2 转向系统初始状态

我司的035CFD3系列悬架承载3.5 t，采用双横臂独立悬架+气囊的结构，主要应用于7 m左右高端商务车，该独立悬架所用转向系统如图1所示。

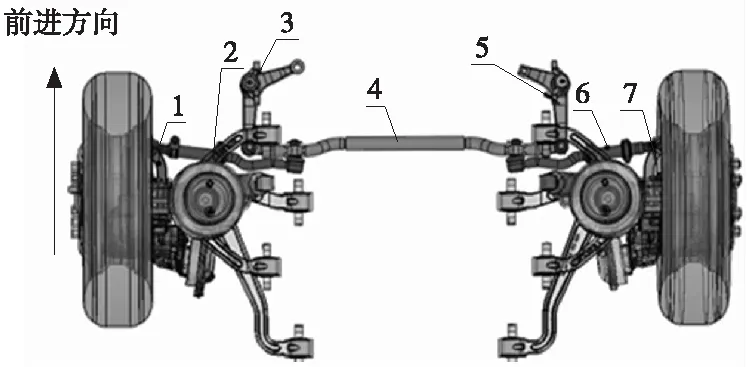
1—左转向节臂； 2—左转向横拉杆； 3—左摇臂； 4—中间横拉杆；5—右摇臂； 6—右转向横拉杆； 7—右转向节臂。图1 断开式转向系统组成

拉杆两端均采用球铰，球头可在一定角度内摆动，杆件之间通过锥孔连接。其中左、右转向横拉杆为相同产品，左、右摇臂对称安装。

左、右转向横拉杆用于调整前束，保证轮胎姿态。以方向机在左侧为例，左摇臂绕中心轴旋转，推动中间横拉杆，中间横拉杆带动右摇臂和左、右转向横拉杆运动，进而推动左、右转向节臂带轮胎偏转，实现转向。

其中，中间横拉杆和左、右转向节臂为锻件已开模，不建议更改；左、右转向横拉杆可调节长短；左、右摇臂及其支架可在X方向移动(车辆前进方向)。

原来的转向系统用于比亚迪C6车型，本次项目应用于宇通某6.9 m商用车，两车型的轴距、车宽不同，导致原内外转角无法满足新车型需求。

实际工作中，用阿克曼校正率RA来评价转角关系：当RA在73%～93%时，内、外前轮侧偏角趋于一致，轮胎的磨损最小。其中，阿克曼校正率RA的定义为[11]：

RA=(θia-θo)/(θi-θo)

(2)

式中：θia是外轮转角为θo时车型的实测内转角。

原车型主销接地点间距1 586 mm,轴距3 935 mm，新车型对应的参数分别为1 685 mm、3 100 mm。在设计过程中，前束应在规定范围内保证轮胎的姿态正确，测量的内、外转角才有意义。将原转向系统直接应用于新车型，仅通过调整左、右转向横拉杆的长度约束前束后，在三维模型上测量轮胎空间转角θia，根据式(1)和式(2)，RA在20%～40%之间。新项目的RA目标是80%以上，相差太远，需要重新调整转向系统，调整的方向是将新结构内转角θia变大。

3 快速调整设计方法及效果

3.1 建立硬点投影模型

过主销点，构建一水平面，将转向系统的硬点投影到该平面上，如图2所示。

1—左转向节臂； 2—左转向横拉杆； 3—左摇臂； 4—中间横拉杆；5—右摇臂； 6—右转向横拉杆； 7—右转向节臂。图2 转向系统硬点投影示意图

3.2 调整参数及效果分析

左、右转向节臂、中间横拉杆是锻件，无法更改。可调整的有：左、右转向横拉杆长度，左、右摇臂前后方向的位置。按照这一思路，暂定改变左、右摇臂在车架上的位置，看能否得到更好的转角匹配结果。左、右摇臂位置改变后，要调整左、右转向横拉杆长度，以保证前束在规定范围内。

以现摇臂在车架上位置为原始点，分别在X方向上，左、右摇臂同时向前移动20 mm(+)、50 mm(+)，向后移动20 mm(-)、50 mm(-)，当左摇臂顺时针转动时，左侧为内转角，右侧为外转角。让左摇臂转动25°，各位置转角示意如图3所示。

1—左转向节臂； 2—左转向横拉杆； 3—左摇臂； 4—中间横拉杆；5—右摇臂； 6—右转向横拉杆； 7—右转向节臂。图3 摇臂各位置转角示意图

分析图3可知，当以左摇臂为输入端，左、右摇臂同时向前、后移动时，右侧轮胎转角(外转角)变化不大，而左侧轮胎转角(内转角)变化明显，会随着左、右摇臂向后移动而增大。即当左、右摇臂同时向后移动时，相同外转角对应的内转角增大，有接近理想的阿克曼曲线的趋势。

由于投影是平面示意图，测量的角度不能完全反应空间角，因此在三维模型中寻找更为合适的位置。

3.3 三维模型调整

直接用三维模型校核转向时，要调整左、右摇臂位置，前束，左、右转向拉杆长度，还需考虑实际空间，过程较为复杂。通过平面转角调整，获得调整趋势，能够指导三维模型调整方向，提高工作效率。

结合平面转角调整结论和实际安装空间，三维模型中需将左、右摇臂同时向后移动。具体调整步骤如下：

1) 在图1的上视图绘制2条线，与轮胎中心线重合，如图4所示，通过测量轮胎中心线与中性面的夹角，可得到轮胎的空间转角。

1—左轮胎中心线； 2—中性面； 3—右轮胎中心线。图4 轮胎中心线与中性面

2) 确定车架上可用空间，在空间范围内，同时移动左、右摇臂。

3) 调整前束，前束在0～2 mm之间，该数值可以通过测量步骤1)中轮胎中心线前后点得到，即图4中0

4) 改变左、右转向摇臂夹角，测量轮胎内、外转角。

经过三维模型调整，在左、右摇臂同时向后移动49 mm时,得到较为理想的转角关系。

经计算，调整后的RA在88%～90%之间，满足新车型的需求。

3.4 测试效果

调整后的悬架转向系统装车后在试验场进行测试，依据标准是汽车操稳性的国标和测评方法[12-13]。测试结果良好。

4 结束语

通过将结构复杂的断开式转向系统投影到二维平面，简化模型，调整可变参数，寻找理想的转角关系趋势，并结合三维模型和实际空间，找到合适的转向系统安装位置，从而简单、快速地调整断开式转向系统，获得良好的转向性能。本文将二维平面图和三维模型相结合的方法，也可应用到其他类似项目设计中。