波动法研究加速旋转薄壁圆环的线性振动特性

林 杰，黄迪山

(上海大学 机电工程与自动化学院，上海 200072)

旋转薄壁圆环在工程中的应用广泛，如工业中高速盘鼓类结构、高速轴承保持架、航空发动机的薄壁空心结构、高速轴端挡圈等。该薄壁结构在加速旋转状态下产生极烈振动，甚至导致损伤等故障。因此，研究加速旋转薄壁圆环的振动问题，可为加、减速过程的薄壁结构的动力学特性提供了理论参考。

静止圆环动力学问题研究已相对成熟。Rao等[1-2]对静止圆环平面内弯曲振动进行研究，并且建立圆环平面内运动方程。Evensen[3]考虑非线性项对静止薄壁圆环平面内弯曲振动的影响。在常速旋转的工况下，对薄壁圆环动力学问题学者们也做了大量的研究。Natsiavas[4]建立薄壁圆环的非线性平面内自由振动方程，并对圆环在低转速和高转速状态下进行动力学研究。Huang等[5-6]考虑旋转状态下圆环科氏力效应，求解圆环在静止与不同转速下的固有频率及振型。 Kim等[7]研究常转速下不同非线性项对圆环固有频率计算的影响。研究表明，在较低转速下不同形式的非线性项所求解出的固有频率基本相同，只有在较高转速下会产生偏差。常速旋转的条件下，王宇等[8]研究蓖齿薄壁短圆柱壳在5种不同边界条件下的行波共振特性。刘彦琦等[9]探讨了薄壁圆柱壳长径比对其振动特性的影响。

现今，对静止和常转速旋转薄壁圆环及圆柱壳的研究已经取得不少理论成果。但是，对加速旋转圆环系统受科氏力、离心力和加速度的影响及其弹性变形等方面的研究才刚起步，相关文献较少[10]。

本文基于Euler -Bernoulli梁理论，考虑科氏力和离心力效应。根据Hamilton原理建立加速旋转薄壁圆环的平面内线性运动方程，运用波动法进行动力学求解，分析角加速度，角速度对薄壁圆环模态特性的影响，并对方程进行验证。

1 运动方程

如图1所示，有一个加速旋转薄壁圆环，其圆环角速度为：

Ω=ct

(1)

式中:c为圆环角加速度，且为常数，所以角速度是关于时间t的线性函数。

XYZ是空间中一个固定的惯性坐标系，而xyz则是固定于微元上相对于XYZ的一个旋转坐标系，沿圆环中性轴的周向坐标由x表示，与中性轴垂直的径向坐标由y表示。圆环横截面中性轴上的周向，径向位移分别用u，v表示。b为圆环的宽度，h为圆环的厚度。M为平面内驱动转矩，由牛顿定律得：

M=J·c

(2)

式中:J为圆环转动惯量。

(a) 全视图

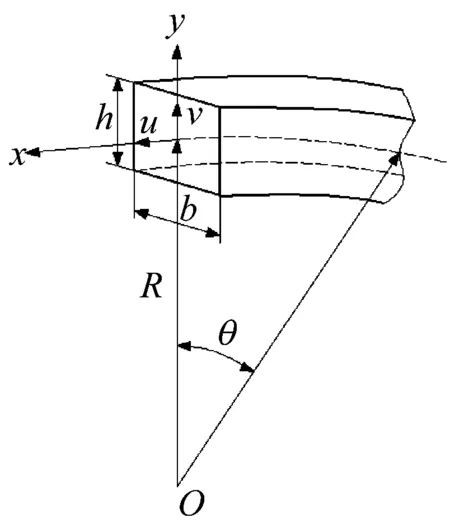
(b) 截面图

基于Euler -Bernoulli梁理论，圆环变形前垂直于圆环中性线的横截面，在变形后仍然垂直于圆环中性线，且横截面的宽度和高度保持不变。薄壁圆环的厚度h和宽度b远小于圆环的半径R，所以不考虑圆环横向剪切变形的影响。

α为平面内弯曲变形引起圆环横截面绕z轴旋转的旋转角。根据Rao和Natsiavas研究，α可表示为：

(3)

基于拉格朗日应变理论，根据Kim和Graff[11]研究可知薄壁圆环中心线上各点的周向正应变包含中性面的应变和平面内弯曲引起的曲率变化，其表达式如下所示：

(4)

式中:第一项为中性面应变，第二项为平面内弯曲引起的曲率变化。

薄壁圆环的应变能和周向正应变有关。假设圆环材料为各向同性，连续且均匀。由于薄壁圆环处于加速和高速旋转状态，需要考虑由离心力作用引起的周向应力所产生的势能。薄壁圆环的应变能可用方程(5)表示：

(5)

式中:E为弹性模量，σθ为离心力引起的初始周向应力。Huang研究表明，σθ可近似表示为ρR2Ω2。

根据Bickford等[12-13]研究表明：薄壁圆环的平面内振动问题中，由于薄壁圆环的厚度远小于圆环半径，薄壁结构的转动惯性力矩可忽略不计。因此，加速旋转薄壁圆环的动能可近似为：

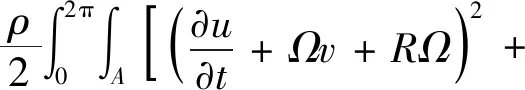
(6)

由于薄壁圆环做加速旋转运动，考虑力矩M做功，其表达式为

(7)

应用Hamilton原理建立加速旋转薄壁圆环的动力学方程，其表达式如下：

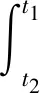
(8)

对方程(8)中第一项进行变分可得：

(9)

式中,Ω=dθ/dt故方程(9)中第三项可表示为：

(10)

方程(8)中第二项进行变分可得：

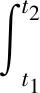
(11)

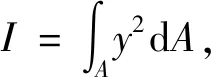
(12)

对方程(8)中第三项进行变分可得：

(13)

由于δv、δu均是独立的任意变量，故只有它们的系数分别等于零时，上式中二次积分才为零。因此，由式(8)～(13)整理可得加速旋转薄壁圆环的平面内运动微分方程，如下所示：

δv:

(14)

δu:

(15)

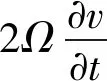
若为静止薄壁圆环，将方程(14)和(15)中角速度Ω项和角加速度dΩ/dt项去除，即可得到静止薄壁圆环平面内径向和周向振动方程，其与Chouvin等14所述的静止薄壁圆环平面内运动方程一致。

2 波动解

采用波动法分析加速圆环的动态特性。波动法是一种联系时间和空间的解析方法。它将结构的自由振动看成弹性波在固体介质中的传播，其自由模态是由各传递波叠加形成。假定运动方程的解是由简谐波分量线性叠加而成，既可以将以时间-空间坐标系为基础的偏微分动力学方程转化为傅里叶级数空间中的代数方程。

假设运动方程的特解为：

(16)

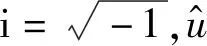
将通解(16)代入方程(14)中，整理后可得：

A1v+A2u=C1

(17)

其中，

同理将通解(16)代入方程(15)中，整理后可得：

A3v+A4u=C2

(18)

其中，

将方程(17),(18)写成矩阵形式得：

(19)

由于结构振动模态是由不同谐波叠加而成，且不同谐波之间是互相独立的。随着波在系统中传播，复波数和虚波数对应的波逐渐衰减为零，只有实波数对应的波才能引起共振模态。因此，当波数n=2,3,4,5时，对应着结构的前四阶模态，而n=0,1为圆环的刚体模态[15]。在求解结构固有频率中，扫频法是较为常用的方法。因此，式(19)给定频率带，可通过扫频法求解薄壁圆环在某一角加速度、角速度和某一阶模态下径向和周向振幅。由此，可得到加速旋转薄壁圆环对应某一阶数下的幅频特性曲线。

3 旋转状态

薄壁圆环的几何尺寸和物理参数，如表1所示。假定Ω=t且t=2π,10π,20π。在波数n=4时，分别求出旋转薄壁圆环在转速Ω=2π,10π,20π rad/s，第三阶的径向振动频率特性。结果如图2所示，图中分别对应角速度为2π rad/s、10π rad/s和20π rad/s时，薄壁圆环第三阶径向振幅。

如表2所示，在不同转速下，将圆环第三阶固有频率求解结果与Eley的结果进行对比，其相对误差值均不超过0.1%。

表1 薄壁圆环的几何尺寸和物理参数

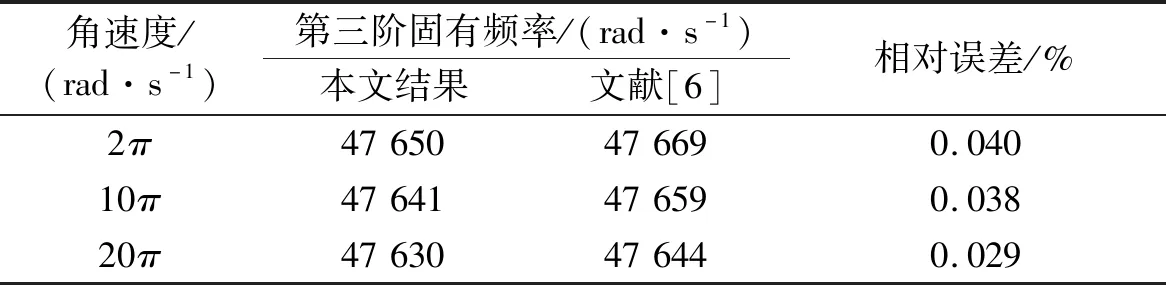
表2 不同角速下度薄壁圆环第三阶固有频率求解结果对比

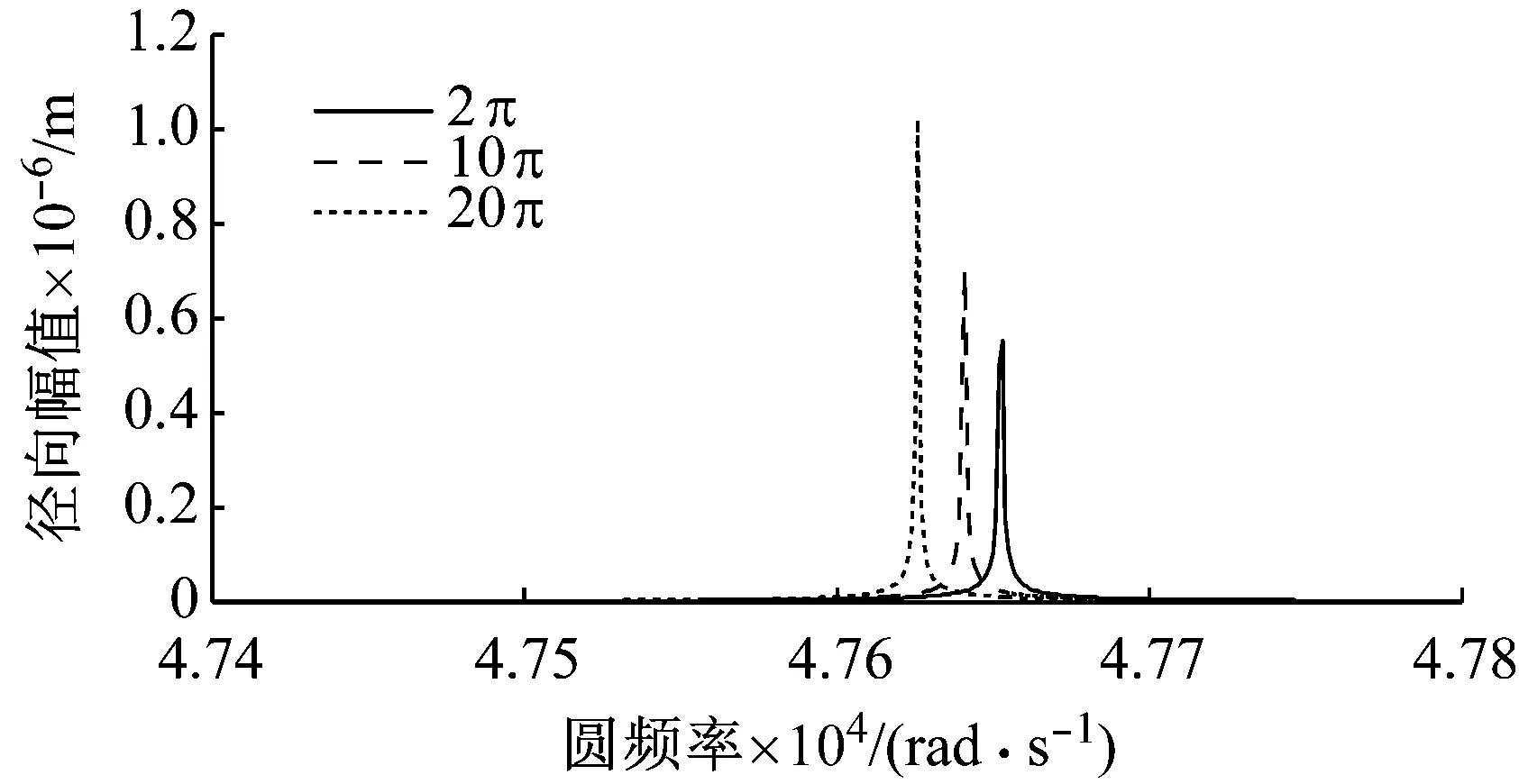
图2 角速度Ω=2π, 10π, 20π rad/s时，薄壁圆环第三阶

4 角速度影响

薄壁圆环的几何尺寸和物理参数，如表3所示。假定Ω=trad/s，角速度随着时间的增加而线性增大。如图3，横轴为频率段、纵轴为角速度、竖轴为薄壁圆环在对应的某特定频率和角速度下的径向振幅。在不同角速度下，前四阶固有频率的计算结果如表4所示。

表3 薄壁圆环的几何尺寸和物理参数

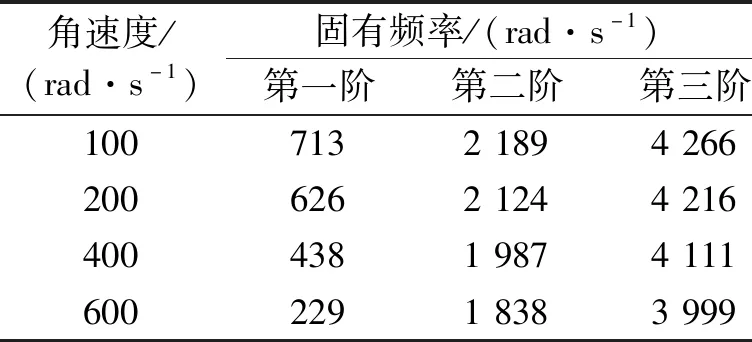
表4 随着角速度增加薄壁圆环的前四阶固有频率

如图3所示，随着角速度的增加，薄壁圆环的前四阶固有频率逐渐减小。当转速达到一定值时，薄壁圆环的固有频率趋于零。该现象与Kim和Eley的研究结果一致，其研究结果表明随着转速增加，负行波的固有频率逐渐减小且趋于零。

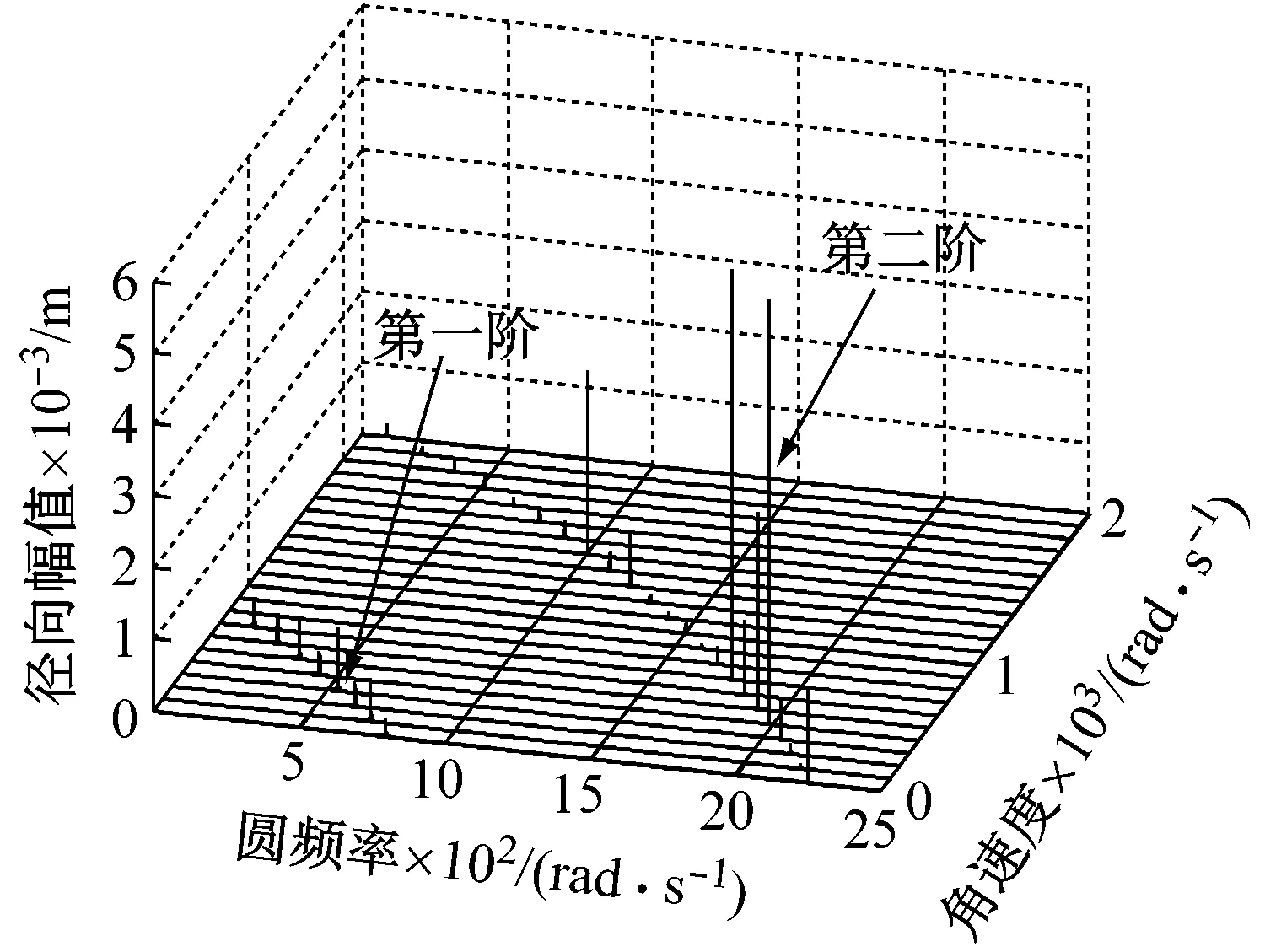
(a) 第一阶和第二阶固有频率变化趋势

(b) 第三阶和第四阶固有频率变化趋势

图3 随着角速度增加，薄壁圆环前四阶固有频率变化趋势

Fig.3 The trend of the ring’s natural frequency at first four orders as the changing of rotational speed

5 角加速度影响

5.1 幅频特性

在某一角速度下，研究薄壁圆环在不同的角加速度下的特性。薄壁圆环的几何尺寸和物理参数，如表3所示。假设角速度为Ω=100 rad/s，分析薄壁圆环在不同的角加速度下的频率特性。如图4，横轴为频率段、纵轴为角加速度、竖轴为薄壁圆环对应某特定频率和角加速度下的径向振幅。不同角加速度下，其前四阶固有频率值所对应的径向幅值如表5所示。

表5 转速为Ω=100 rad/s时，在不同角加速度下薄壁圆环的前四阶固有频率所对应的径向振幅

Tab.5 Radial amplitude corresponding to the first four natural frequencies whenΩ=100 rad/s in different angular acceleration

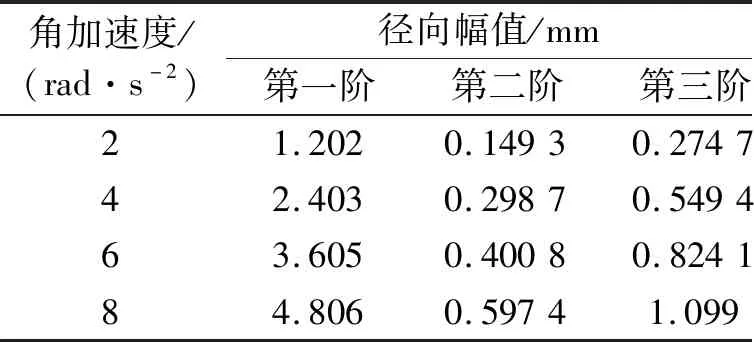
角加速度/(rad·s-2)径向幅值/mm第一阶第二阶第三阶第四阶21.2020.14930.27470.472842.4030.29870.54940.945563.6050.40080.82410.141884.8060.59741.0990.1891

如图4所示，在不同的角加速度下，将薄壁圆环加速至角速度为Ω=100 rad/s时，其前四阶固有频率始终保持不变，分别为713 rad/s、2 189 rad/s、4 266 rad/s和6 938 rad/s。根据图4和表5结果所示，随着角加速度的增加，固有频率保持不变，但圆环各阶固有频率所对应的径向振幅随之增加。因此，角加速度的变化不影响圆环的固有频率，只对其振幅产生影响，且角加速度越大其振幅越大。

(a) 第一阶

(b) 第二阶

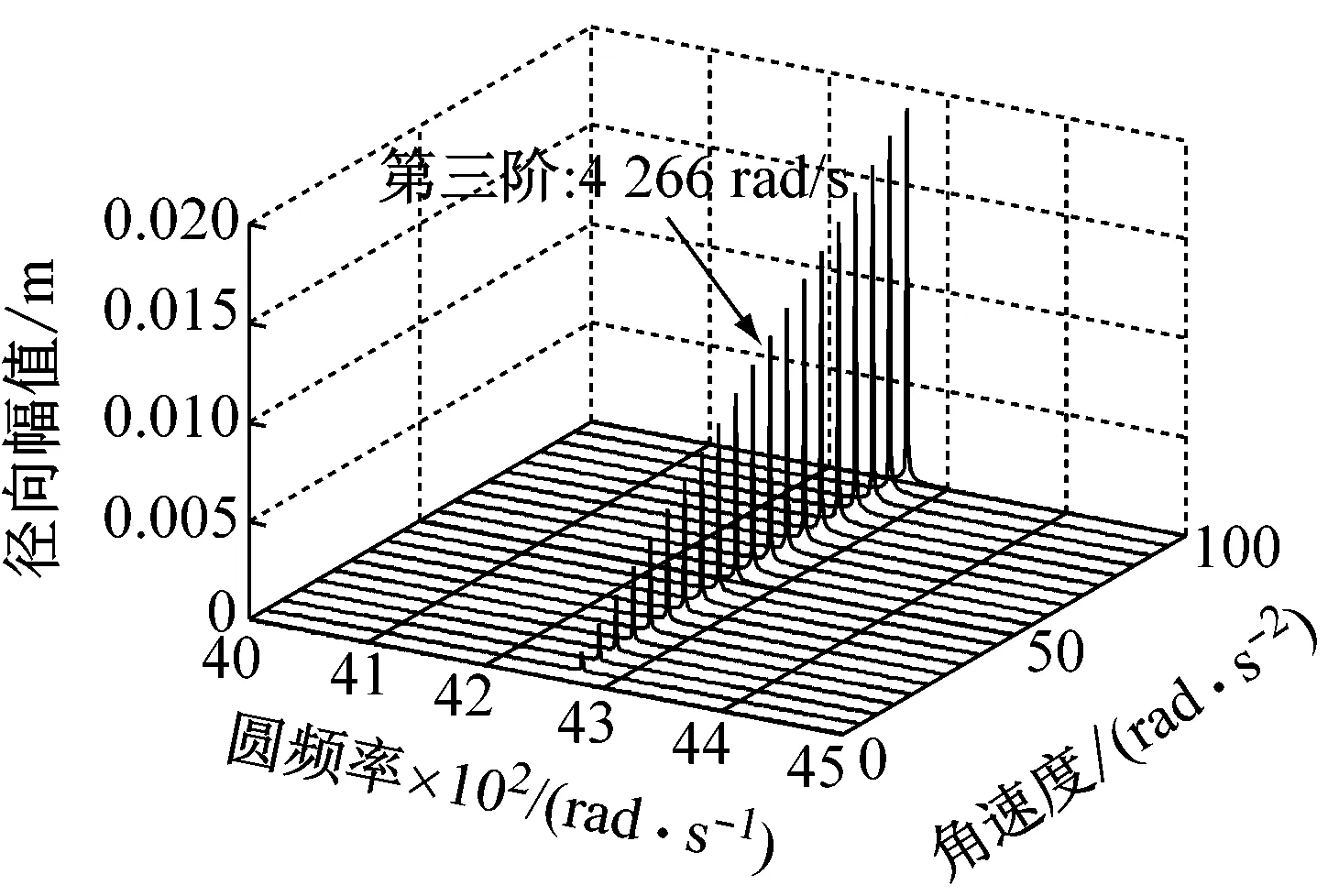
(c) 第三阶

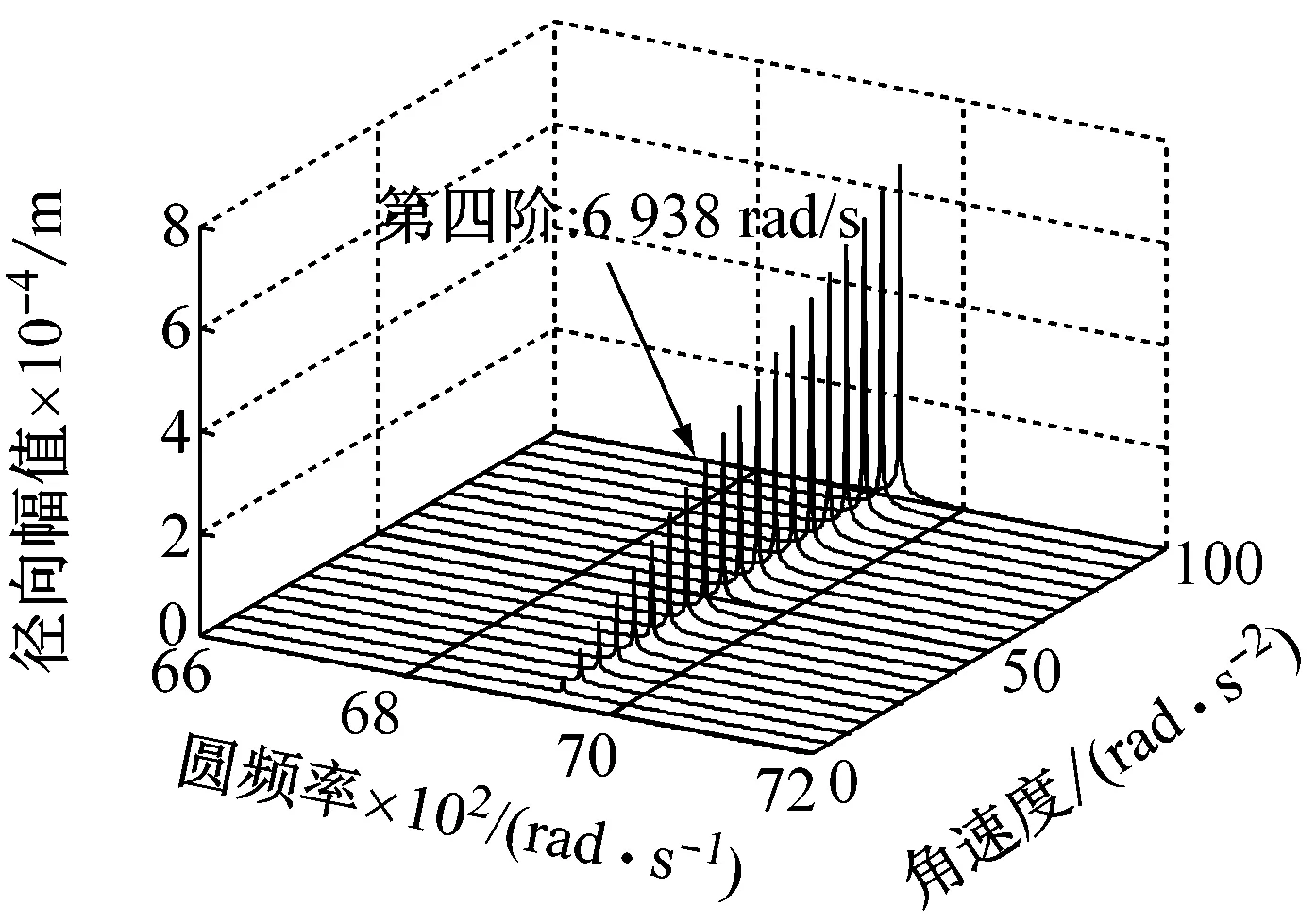
(d) 第四阶

图5所示，更加清楚显示薄壁圆环在不同角加速度下前四阶固有频率对应的径向振幅的变化趋势，其中横轴为角加速度，竖轴为对应某一阶固有频率的径向振幅，虚线为径向幅值增长率曲线。

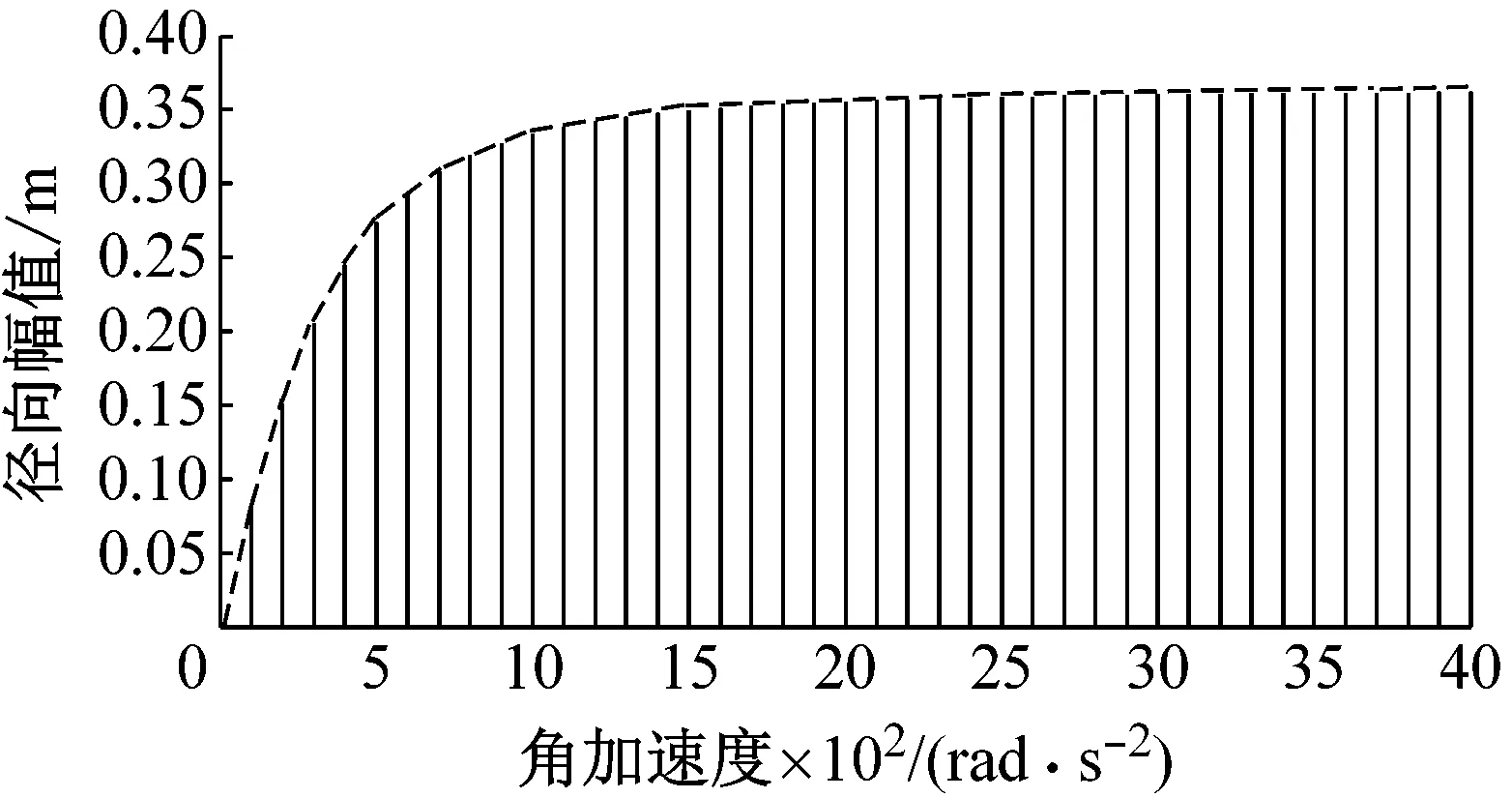
(a) 第一阶

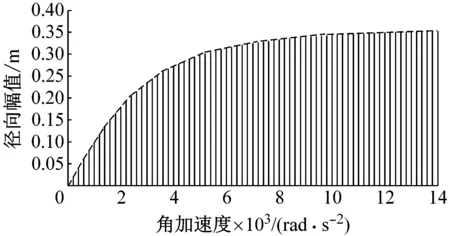
(b) 第二阶

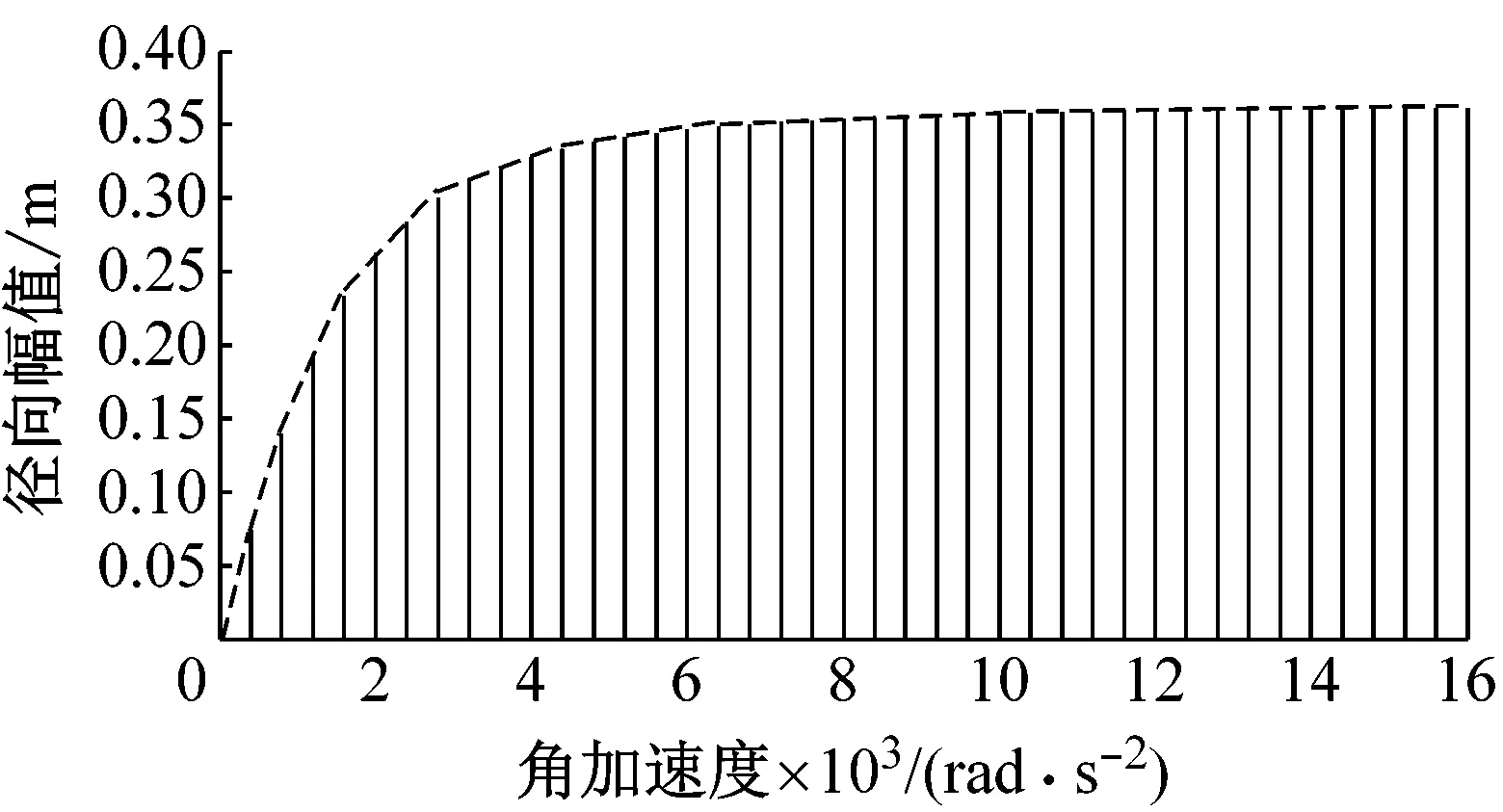
(c) 第三阶

(d) 第四阶

当薄壁圆环的角加速度不断增大时，各阶固有频率对应的径向振幅不断增大，且达到临界角加速度值时其径向幅值增长趋势明显趋于平缓。如图5(a)～(d)所示，当薄壁圆环角加速度分别达到1 500 rad/s2、10 000 rad/s2、6 000 rad/s2、30 000 rad/s2时，其前四阶固有频率对应的径向振幅增加幅度趋于平缓。

5.2 各阶模态

如表5所示，当转速为Ω=100 rad/s，将角加速度为2 rad/s2、4 rad/s2时所对应的前四阶固有频率，以及径向振幅代入方程(16)，计算出加速旋转薄壁圆环的径向振型。图6中虚线和实线分别代表角加速度等于2 rad/s2和4 rad/s2时的模态。

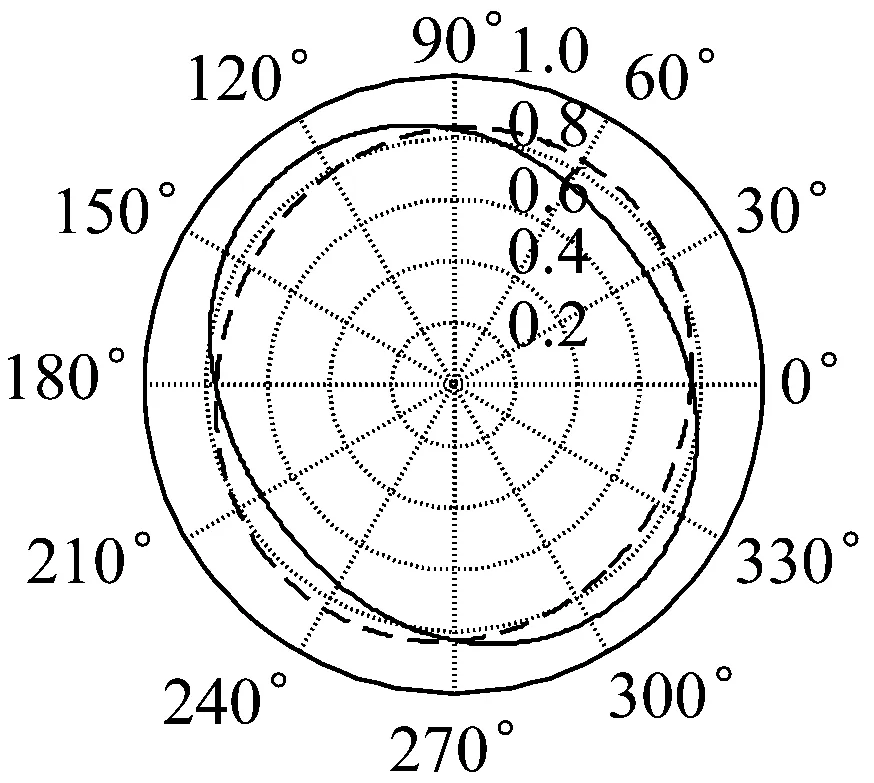
(a)

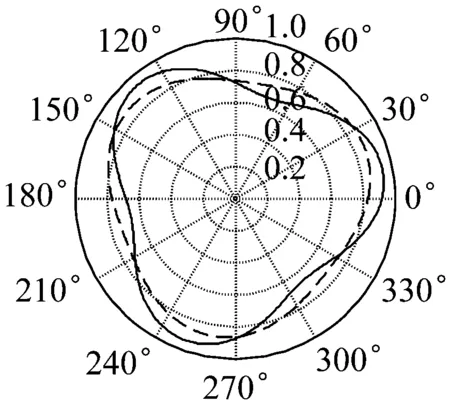
(b)

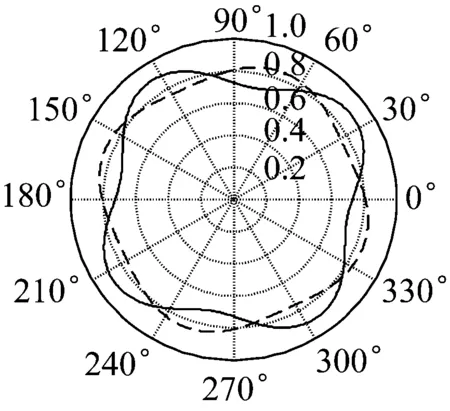
(c)

(d)

图6 转速Ω=100 rad/s时，不同角加速度下薄壁圆环的前四阶径向模态形状(a～d分别为圆环的前四阶模态形状:实线和虚线分别为角加速度c=4 rad/s2和c=2 rad/s2)

Fig.6 Radial mode shapes of thin ring at two different angular accelerations, whenΩ=100 rad/s(a～b the 1st～ 4thradial mode shapes:Solid line is atc=4 rad/s2, Dotted line is atc=2 rad/s2)

在相同的转速下，角加速度越大薄壁圆环的某一阶固有频率所对应的振型越明显。

6 结 论

基于Euler -Bernoulli梁模型，考虑由薄壁圆环加速旋转引起的离心力和科氏力效应，分别给出加速旋转薄壁圆环系统的动能、势能以及外力做功，然后利用Hamilton原理建立加速旋转薄壁圆环系统的平面内线性振动微分方程。利用波动法分析加速薄壁圆环周向和径向振动特性。通过假设圆环在角速度分别为2π rad/s、10π rad/s、20π rad/s时，求解其第三阶固有频率并与相关文献对比，结果表明固有频率相对误差均小于0.1%。

研究角速度与角加速度对薄壁圆环模态特性的影响:① 保持圆环角加速度不变而角速度逐渐增加，薄壁圆环各阶固有频率逐渐降低。当角速度达到临界速度时，薄壁圆环的第一阶固有频率为零，运动进入失稳状态；② 具有不同角加速度的圆环加速至同一转速时，圆环对应同一阶的固有频率值均相同，但固有频率所对应的振幅随着角加速度的增大而增大。因此，角加速度变化只影响薄壁圆环的振幅，而不影响其固有频率。③ 当圆环超过临界角加速度值时，其振幅增长趋于平缓。④ 在相同转速下，角加速度越大的圆环，其各阶振型越明显。

对加速旋转薄壁圆环进行研究，揭示了角加速度和角速度对旋转薄壁圆环结构模态特性的影响，文中提供了求解该系统固有频率和振型的波动计算方法。为加速过程或运转起动阶段的薄壁圆环结构的动力学研究提供了理论参考。