分形粗糙表面加卸载接触特性演变行为分析

刘楷安，徐颖强，吴正海，李万钟

(西北工业大学 机电学院，西安 710072)

粗糙表面的接触行为对摩擦、磨损、润滑、密封和传热等具有重要的影响，已经成为摩擦学中重要的研究课题之一[1]。接触问题的加卸载现象，引起接触载荷、接触面积和变形量的非线性变化，并对接触表面形貌参数与接触力学性能产生重要的影响。如何解决单个微凸体力学行为与真实接触表面加卸载接触特性的内在联系非常必要。因此，本文针对粗糙表面加卸载接触问题，研究其接触特性与形貌参数演变具有重要的意义。

目前，国内外学者对粗糙表面的表征方法与接触分析做了大量的研究。在理论解析模型方面，先后构建了GW模型[2]、W-A模型[3]、CEB模型[4]、MB模型[5]等，这些模型均依赖于一定的假设条件，如微凸体具有相同的曲率半径、微凸体发生小变形且相互独立、忽略材料的非线性特点等。上述模型的假设条件与简化处理在一定程度上影响了粗糙表面接触分析的准确性，因此采用有限元数值模拟成为一种有效的方法。Kogut等[6-7]采用有限元法对刚性平面与弹塑性球体接触进行了数值模型。Kogut和Jackson分别表征了刚性平面与微凸体接触弹塑性变形机制，已成为粗擦表面接触理论分析的基础而被广泛使用。Sellgren等[8]建立粗糙表面接触有限元模型，分析了表面粗糙度、微凸体曲率半径等参数对接触面积与应力分布状态的影响。Sellgren建立的分析模型为刚性球体与不同等级的粗糙表面接触，与真实的粗糙表面接触存在一定的距离，但是其分析方法具有一定的借鉴意义。李辉光等[9]建立有限元模型，研究微元体粗糙表面的接触特性。肖会芳等[10]将有限元模型与动力学方程结合，研究分形粗糙表面的界面接触振动与能量耗散问题。Yan等[11]提出了三维分形力学理论，采用数值方法建立了平均接触压力、接触面积与平均表面分离距离之间的关系。Sahoo等[12]根据W-M分形函生成粗糙表面形貌数据，建立分形表面与刚性平面接触有限模型，分析弹性接触过程中分形参数对接触面积、变形量的影响。文献[9-12]采用有限元法，建立了精确的数值求解模型，对接触刚度、动力学问题以及接触特性进行了研究。Yan和Sahoo结合分形理论，采用实验与数值模拟的方法，对加载过程的接触特性进行了研究，给出的分形参数被众多学者建模分析引用。

粗糙表面加卸载接触特性的研究文献相对较少，主要集中在理论分析与单个微凸体的加卸载特性研究。陈建江等[13]基于分形理论建立了粗糙表面接触加卸载解析模型，获得加卸载过程中粗糙表面接触面积与接触载荷之间的关系。Etsion等[14]采用有限元法研究刚性平面与球体弹塑性接触的加卸载过程，给出了接触载荷、接触面积与变形量的量纲一表达式。Etsion建立的加卸载过程微凸体变形机制成为研究粗糙表面加卸载特性的基础。文献[15-16]分析了弹塑性球体和刚性平面黏结接触的加卸载接触特性。Kadin等[17]提出一种粗糙表面弹塑性接触卸载的统计学模型，分析卸载后粗糙表面的残余形貌并给出粗糙表面高度分布函数。陈建江和Kadin的模型都是建立在Etsion模型的基础上，分别研究了分形模型和统计模型的加卸载特性。Etsion模型中微凸体的最大变形量为临界变形量的110倍，上述两个模型都未考虑微凸体间的相互影响与超出最大变形量的接触行为。

综上所述，对于粗糙表面弹塑性接触问题，研究者大多基于统计学或分形理论从单个微凸体拓展到整个粗糙表面进行研究，采用的方法则是基于Kogut和Etsion提出的微凸体变形机制，往往存一定的局限性。本文基于分形理论和弹塑性理论，对分形粗糙表面进行数字化表征并建立精确的有限元模型，探讨加卸载过程中分形参数对接触面积、变形量和表面形貌的影响，并从分形参数和能量角度揭示上述演变行为的内在机理，对进一步研究粗糙表面接触力学性能和界面载荷传递效率与增强机理具有重要的意义。

1 基本理论

两个粗糙表面的接触问题，可以用一个等效的粗糙表面与刚性平面接触来替代。如图1所示，以粗糙表面微凸体平均高度线为基准，z表示微凸体峰顶的高度，d表示刚性平面相对基准的距离。

图1 粗糙表面接触状态示意图

刚性平面由位置1变化到位置2，粗糙表面微凸体的接触状态与卸载规则取决参数z与d的大小，即加卸载过程中粗糙表面上不同高度的微凸体接触状态不同。区域Ⅰ微凸体产生弹塑性变形，卸载时出现弹塑性变形或完全塑性变形；区域Ⅱ微凸体为完全弹性变形，卸载时微凸体轮廓恢复到加载前的初始状态；区域Ⅲ微凸体未发生接触，不产生接触力，若不考虑微凸体之间的相互影响，则该区域微凸体不影响刚性平面与粗糙表面间的接触行为。

1.1 单微凸体加卸载模型

粗糙表面接触的加卸载过程是一个高度复杂的非线性问题，以下给出单个微凸体的加卸载模型。如图2所示，P为刚性平面载荷，ω和a为微凸体接触变形量和接触半宽；ωmax和amax为完全加载时最大接触变形量和最大接触半宽；ωres为完全卸载时残余接触变形量；R为微凸体峰顶原始曲率半径；Rres为完全卸载残余轮廓峰顶曲率半径。

图2 微凸体加卸载变形示意图

如图2所示，随着刚性平面载荷的增加，微凸体依次经历完全弹性变形、弹塑性变形和完全塑性变形等三种接触状态[18]。当微凸体出现初始屈服点时，其对应的临界变形量、接触载荷及接触面积分别为：

(1)

(2)

Ac=πRωec

(3)

式中：K为硬度系数，与材料的泊松比v有关，且有K=0.454+0.41v；H为较软材料的硬度；E′为等效弹性模量，且有E′=E/(1-ν2)，E为微凸体材料的弹性模量。

1.1.1 弹性接触

当接触变形量ω<ωec时，由Hertz理论[19]，微凸体发生完全弹性变形，接触载荷和接触面积分别为：

(4)

单个微凸体卸载规则：发生完全弹性变形的微凸体卸载后恢复到初始状态，即峰顶曲率半径和高度与加载前完全一致。

1.1.2 完全塑性接触

当接触变形量ω>ωpc时，微凸体发生完全塑性变形，Kogut等给出ωpc的值为：

ωpc=110ωec

(5)

在此阶段，微凸体发生完全塑性变形，接触载荷和接触面积为：

P′=2πRωH,A′=2πRω

(6)

单个微凸体卸载规则：不考虑微凸体的相互影响，发生完全塑性变形的微凸体卸载时，微凸体轮廓与完全加载时一致。

1.1.3 弹塑性接触

当接触变形量ωec≤ω≤ωpc，微凸体发生弹塑性变形，Etsion等研究表明微凸体接触状态分为两个阶段：当ωec≤ω≤6ωec，微凸体变形属于第一弹塑性阶段；当6ωec≤ω≤110ωec，微凸体变形属于第二弹塑性阶段。经数值模拟与曲线拟合，弹塑性接触的接触载荷和接触面积分别为：

(7)

(8)

卸载过程中的接触载荷和接触面积分别为：

(9)

(10)

(11)

微凸体峰顶原始曲率半径R和完全卸载轮廓峰顶曲率半径Rres关系为：

(12)

(13)

(14)

如图3所示，弹塑性接触微凸体在加卸载过程中，量纲一残余变形量随最大变形量非线性增加，量纲一残余轮廓半径与最大变形量呈线性关系。

图3 卸载轮廓参数与最大变形量关系

1.2 Prandtl-Reuss(P-R)塑性理论

分形粗糙表面接触发生弹塑性变形，有限元模型基于Prandtl-Reuss本构关系进行求解。在P-R塑性理论中，体积应变是弹性的，塑性区域的应变增量可分为弹性部分和塑性部分，塑性的应变公式为：

Δε=Δεe+Δεp

(15)

式中：Δεe为弹性应变增量;Δεp为塑性应变增量。

弹性部分满足Hook定律，则弹性应变增量为:

Δεe=De-1Δσ

(16)

式中：De-1为材料的弹性矩阵;Δσ应力增量。

塑性部分满足关联流动规律，则有：

(17)

式中：Y为加载面;dλ为关联塑性参数。

对于Mises屈服材料，应力增量与应变增量的关系式为：

Δσ=DepΔε

(18)

式中：Dep为弹塑性矩阵，且有

(19)

式中：I为单位矩阵;σM为Mises屈服强度;Hp为单轴应力与塑性应变曲线的斜率。

显然，弹性与塑性的应力应变关系有：

Δσ=DΔε

(20)

式中：D为弹塑性系数，在弹性区域D=De，在塑性区域D=Dep。

由弹塑性力学可知，弹性应变能密度和塑性应变能密度分别为：

(21)

(22)

将弹性应变能密度和塑性应变能密度对整个体积积分可以得到弹性应变能和塑性应变能，其和为总应变能，可以表述为：

(23)

式中：W为总应变能;We为弹性应变能;Wp为塑性应变能;V为体积。

2 粗糙表面数字化表征

基于分形理论，Yan和Komvopoulos提出了修正Weierstrass-Mandelbrot(W-M)函数用于三维分形表面的描述，其表达式为：

(24)

式中：z(x,y)为粗糙表面轮廓高度;L为样本长度;Ls为截断长度;D为分形维数(21)缩放参数；n为频率因子，且nmax=int[log(L/Ls)/logγ]；M为分形表面的脊线数；φm,n为[0 2π]的随机相位。

根据Yan等的实验研究，分形粗糙表面参数分别取D=2.5，G=1.36×10-12m，L=9×10-7m,Ls=1.5×10-7m,M=10，γ=1.5，结合公式(24)，采用Matlab软件编程生成点云数据构造三维分型表面，如图4所示。

3 有限元模型

采用APDL编程处理点云数据，经过Coons patch曲面拟合与布尔运算，生成三维分形粗糙表面实体，由粗糙表面最高点确定刚性平面Z向位置，建立接触有限元模型，如图5所示。定义单元类型为8节点Solid185单元，该单元具有计算超弹性、应力强化、大变形和大应变的能力。选择双线性等向强化非线性材料，材料属性见表1。采用von Mises屈服准则判断弹性变形和塑性变形间的转变，通过Prandtl-Reuss本构关系控制塑性区域的应力应变状态。将刚性平面定义为目标面，金属体粗糙面定义为接触面，使用TARGE170和CONTA174单元建立面-面接触对。金属体下表面添加全约束，刚性平面通过控制节点约束且仅具有Z方向自由度。接触算法采用增广Lagrange算法，可以有效地控制表面之间的穿透，设置力的收敛准则为0.001。通过控制节点施加载荷，其数值随求解载荷子步按斜坡曲线依次递增，最大载荷步和最小载荷步为200和10。

图4 三维分形粗糙表面

表1 粗糙表面材料属性

图5 分形表面接触有限元模型

4 接触特性分析

4.1 加卸载特性

根据Yan等的实验数据，选择分形维数D的范围为2.4～2.7，尺度参数G的范围为1.36×10-13m～1.36×10-10m。设置2个分析条件研究分形参数对加卸载接触特性的影响。条件1：施加载荷F=4×10-4N，尺度参数为G=1.36×10-12m，分形维数为变量；条件2：施加载荷F=4×10-4N，分形维数为D=2.5，尺度参数为变量。

图6显示，加卸载过程中，接触面积随接触载荷非线性递增，非线性程度与分形维数与接触行为有关。在相同载荷下，随着分形维数的增加，接触面积依次递增且存在明显的差异，例如，分形维数D=2.7～2.5的最大接触面积分别是D=2.4的12.25、5.45、2.53倍。在卸载过程中，接触面积相比加载过程存在一定的迟滞现象，即出现相同的接触面积，卸载时的载荷比加载时小，与Kadin等的结论一致。

图6 量纲一接触面积与载荷关系(G=1.36×10-12 m)

Fig.6 Dimensionless contact area versus dimensionless load for varyingDatG=1.36×10-12m

图7显示，变形量在加卸载过程中随接触载荷的增加非线性递增。随着分形维数的增加，变形量则依次递减，例如，分形维数D=2.4～2.6的最大变形量分别是D=2.7时的10.64、4.58、2.10倍。残余变量是指卸载后刚性平面相对于加载初始位置的变形量。图7显示，分形维数越大最大变形量越小，残余变形量越小，如D=2.4～2.6的残余变形量是D=2.7的13.94、5.43、2.222倍。对比图3可知，分形表面残余变形量与最大变形量间关系与单个微凸体的规律一致。

图7 量纲一变形量与载荷关系(G=1.36×10-12 m)

Fig.7 Dimensionless displacement versus dimensionless load for varyingDatG=1.36×10-12m

图8显示，不同尺度参数的粗糙表面，接触面积随载荷非线性增加，其非线性程度与尺度参数有关。相同载荷下，随着尺度参数的增加，接触面积逐渐减小，例如，分形维数G=1.36×10-13m～1.36×10-11m的最大接触面积分别是G=1.36×10-10m的10.42、5.99、2.66倍。由分形理论可知，尺度参数越小表面则越光滑，更多的表面微凸体进入完全塑性阶段，则接触面积与接触载荷的非线性程度变弱，与公式(6)反映的规律一致。

图8 量纲一接触面积与载荷关系(D=2.5)

Fig.8 Dimensionless contact area versus dimensionless load for varyingGatD=2.5

图9显示，在加卸载过程中，变形量随载荷非线性增加，不同尺度参数分线性程度差异明显。随着尺度参数的增加，变形量及残余变形量都逐渐增加，例如，尺度参数G=1.36×10-10m～1.36×10-12m的最大变形量分别是G=1.36×10-13m的11.57、4.80、2.26倍。尺度参数G=1.36×10-10m～1.36×10-12m的残余变形量分别是G=1.36×10-13m的14.08、5.27、2.55倍。

图9 量纲一变形量与载荷关系(D=2.5)

Fig.9 Dimensionless displacement versus dimensionless load for varyingGatD=2.5

对比图6～图9，不同分形参数的粗糙表面卸载过程中，接触面积和变形量相对加载过程存在一定的迟滞现象，其程度与接触面积和变形量的最大值正相关。图6、图8显示，加载过程接触面积与载荷近似线性关系，卸载非线性更为明显。卸载时，粗糙表面微凸体的接触状态可认为是卸载表面加载完全弹性接触的逆过程[14]，即卸载过程为弹性接触。图7、图9显示，分形维数越大，尺度参数越小，变形量与载荷近似线性关系，反映的表面接触刚度越大，接触表面具有更好的加卸载特性，与Sahoo等的结论一致。

4.2 表面形貌演变规律

针对粗糙表面形貌参数的随机性特点，采用概率密度函数研究分形表面加卸载过程形貌参数演变是一种有效的方法。同时，分形参数的多样性也导致确定分形表面高度分布类型存在一定的难度。在此，采用适于处理未知密度函数的核密度估计法(Kernel density estimation)建立不同接触状态表面形貌高度参数的概率密度函数。由图1可知，粗糙表面接触引起区域Ⅰ、区域Ⅱ内的微凸体高度发生变化，而区域Ⅲ的高度不受影响。在概率密度函数曲线上，接触区域微凸体对应的高度区间及相邻区间在加卸载过程中会发生变化，而远离接触区域的高度区间则不发生改变。因此，概率密度函数蕴含着加卸载过程中表面形貌参数演变信息。取原始表面法向高度的平均值作为参考值，对上述原始表面、加载表面、卸载表面的形貌高度参数进行量纲一化。

图10显示，分形维数不同的表面，其高度参数的概率密度函数曲线之间存在很大差异。相同载荷下，随着分形维数增大，接触行为对表面形貌高度的影响区域增大。分形维数D=2.4，概率密度函数曲线只在右侧发生局部改变。对应初始、加载、卸载接触状态的偏态值为-0.11，-0.22，-0.18，峰态值为1.97，1.91，1.92；分形维数D=2.7，概率密度函数曲线整体发生较大变化，偏态值分别为0.11，-0.64，-0.20，峰态值为2.11，3.03，2.27。由分形理论可知，分形维数越大反映粗糙表面形态越密集，即微凸体的数量多。分形维数较小时，发生接触行为的微凸体数量较少，而其余的微凸体未发生改变，在概率密度函数曲线上体现为局部发生变化，反之亦然。

(a) D=2.4

(b) D=2.5

(c) D=2.6

(d) D=2.7

图10 不同分形维数表面高度概率密度函数(G=1.36×10-12m)

Fig.10 Probability density function of surface height with different fractal dimension (G=1.36×10-12m)

图11显示，尺度参数不同，表面高度的概率密度函曲线存在很大的差异。加卸载过程中，随着尺度参数的增大，概率密度函数曲线变化程度逐渐减弱。尺度参数取较小值时，不同接触状态的概率密度函数曲线差异更为明显。例如：尺度参数G=1.36×10-13m的偏态值分别为0.11，-0.47，-0.22，峰态值分别为2.06，1.99，1.92；尺度参数G=1.36×10-10m的偏态值分别为0.16，0.06，0.09，峰态值分别为2.27，2.14，2.17。与分形参数的影响不同，尺度参数只是不同程度改变概率密度函数曲线右侧，即表面高度较大的区域。由分形理论，尺度参数为表面的特征长度参数，只反映分形表面映幅值的大小，不影响微凸体的空间密度。因此，在尺度参数变化时，接触行为只影响到数量较少的微凸体。

(a) G=1.36×10-13 m

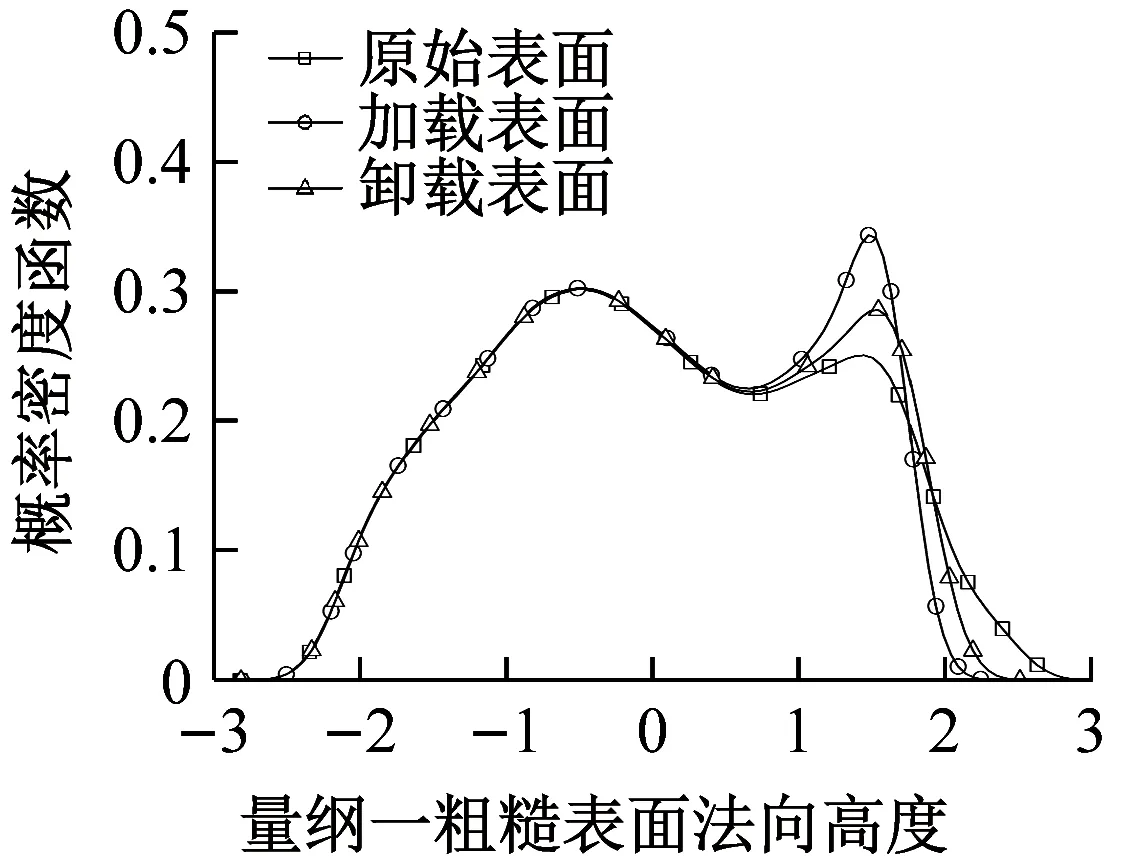
(b) G=1.36×10-11 m

(c) G=1.36×10-10 m

图11 不同尺度参数表面高度概率密度函数(D=2.5)

Fig.11 Probability density function of surface height with different scale parameters (G=1.36×10-12m)

通过对有限元模型结果的处理，统计加卸载过程中粗糙表面形貌数据，计算分形参数变化时不同接触状态的表面粗糙度。表2为粗糙表面加卸载过程中，不同分形维数和尺度参数对表面粗糙度的影响。ΔL表示加载表面相对初始表面粗糙度变化的绝对值，ΔU表示卸载表面相对于加载表面粗糙度变化值。

表2 分形参数对粗糙度的影响

由表2可知，随着分形维数的增加与尺度参数的减小，粗糙表面则越光滑。在相同载荷作用下，随着表面粗糙度的减小，加卸载过程中粗糙度值的变化量越小。显然，表面粗糙度的变化，能够反映了粗糙表面加卸载特性。当尺度参数G=1.36×10-12m，分形维数G=2.4～2.7时，卸载与加载状态粗糙度相对变化比值ΔU/ΔL分别是0.40、044、0.47、0.91。当分形维数D=2.5，尺度参数G=1.36×10-13m～1.36×10-10m时，卸载与加载状态粗糙度相对变化比值ΔU/ΔL分别是0.49、0.44、0.43、0.34。结合4.1接触特性分析，可知ΔU/ΔL比值越大，反映卸载过程中弹性恢复能力越强，表面具有更好的加卸载特性。保持尺度参数不变，分形维数D大于2.6时，分形表面加卸载性能快速提升；分形维数不变，尺度参数小于G=1.36×10-13m时，分形表面具有更好的加卸载特性。

4.3 应变能变化

加卸载过程中，伴随着接触参数与表面形貌的改变，金属体发生弹塑性变形，其应力状态应也随着接触状态的不同而发生改变。图12为粗糙表面在加载和卸载状态下，分形表面的Von Mises应力在Z轴的投影。显然，其应力状态与粗糙表面微凸体的高度与接触状态有关。结合4.1定义的条件，分析分形参数改变时不同接触状态应变能的变化规律。为便于分析，做量纲一化处理：以加载时最大应变能为参考值，将加载应变能和卸载应变能量纲一化。应变能变化是指卸载应变能相对加载应变能的变化量，采用对应的加载应变能作参考值进行量纲一化。

(a) 原始表面

(c) 卸载表面

图12 接触表面Von Mises应力分布(D=2.5,G=1.36×10-12m)

Fig.12 Von Mises stress distribution on contact surfaces (D=2.5,G=1.36×10-12m)

图13显示，加载应变能和卸载应变能随分形维数增加而减小，随尺度参数的增加而增加，而应变能变化量则与之相反，其变化范围为0.3～0.55。对比图7，图9可知，相同载荷作下，金属体的加载应变能和卸载应变能主要取决于变形量和残余变形量的值。表面越粗糙，变形量越大，则加载应变能、卸载应变能和能量耗散越大，反之亦然。显然，相同载荷下，光滑表面加载应变能和卸载应变能更小，且能量耗散少，同时，卸载时相对于加载应变能的变化量更大，即能量释放能力更强。

(a) 分形维数变化

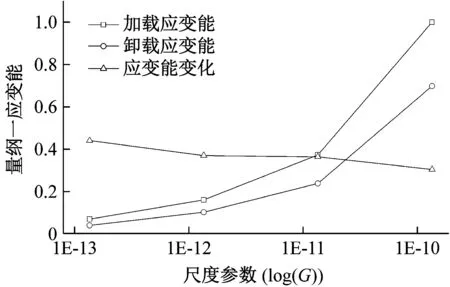
(b) 尺度参数变化

图13 应变能与分形参数关系

Fig.13 The relationship between strain energy and fractal parameters

5 结 论

(1) 分形粗糙表面与刚性平面接触，分形表面和尺度参数对接触面积和变形量存在较大的影响。分形维数卸载过程中，接触面积和变形量相比加载过程存在一定的迟滞现象，其程度与接触面积和变形量的最大值正相关。

(2) 随着分形维数增大，接触行为对表面形貌的影响增强；随着尺度参数的增加，接触行为对表面形貌的影响减弱；相比分形维数，尺度参数仅影响局部表面高度参数。分形维数D大于2.6时，尺度参数G小于G=1.36×10-13m，分形表面具有更好的加卸载性能。

(3) 从能量角度进一步揭示了光滑表面具有更好接触性能和传递效率的机理。即相同载荷下，表面越光滑，加卸载过程应变能和能量耗散越小，且卸载过程中应变能的相对变化量大。