高速齿轮传递误差和啮入冲击的激励模拟及齿面优化修形

贾 超，方宗德

(1.福州大学 机械工程及自动化学院，福州 350108； 2.西北工业大学 机电学院，西安 710072)

齿轮传动是机械装备的重要构件之一，其设计和制造技术在一定程度上代表了一个国家的制造业水平。通过齿面修形来实现减振降噪在齿轮设计中始终占有重要地位。Litvin等[1]通过改变刀具齿廓和刀具与加工齿面之间的运动关系，得到修形齿面，并完成齿面接触分析。Bruyère等[2]通过齿廓修形降低了窄齿面直齿轮的传动误差，并通过动态分析验证了修形效果。Korta等[3]通过响应面法对齿面进行了优化修形，降低了传动误差幅值和齿面接触应力。贾超等[4]完成了高速内啮合人字齿轮的多目标优化修形，齿面修形后，承载传动误差幅值下降，啮入区和啮出区闪温降低，齿面载荷分布得到了改善。詹东安等[5]分析了高速齿轮传动的特点和齿部修形原因，研究了高速齿轮齿部修形的设计原则与计算修形量的经验公式。Yuan等[6]研究了对角修形对斜齿轮系统的准静态及动态的影响。

关于齿轮传动的减振降噪研究，其激励分析是首要任务，多年以来已经有许多关于激励分析的文献发表。大量的理论和试验研究表明，齿轮传动误差和啮合冲击是首要激励源，其它如齿侧间隙、齿轮加工安装误差，以及齿面摩擦等，都是齿轮传动中的激励，而齿轮减振降噪技术就是通过减少激励和降低响应来抑制齿轮传动中的振动，其中减少激励是最根本的措施。实际上，齿侧间隙和齿轮加工安装误差仅是引起振动改变的条件，如果没有其它激励则不会产生剧烈振动，例如齿轮加工安装误差产生附加的传动误差和啮合冲击往往使振动激励增大；而侧隙的存在则使振动产生非线性。齿面摩擦主要是由于在节线上发生摩擦力方向改变而导致激励，在直齿轮传动中有一定影响，而在斜齿轮和人字齿轮传动中影响不明显。传动误差和啮合冲击是齿轮振动最重要的激励，齿面修形的直接目标，就是减少传动误差和啮合冲击的激励作用。王峰等[7-8]建立了考虑啮入冲击力的动力学模型，完成了多载荷工况下的人字齿轮传动系统的振动特性分析。张金梅等[9]对考虑啮入冲击作用下减速器的振动和噪音进行了分析。Höhn等[10]通过齿面修形减小了传动误差幅值，同时提高了啮合效率。Munro等[11]完成了直齿轮对发生线外啮合时的传递误差的分析计算。Yu等[12]对齿轮啮合过程中的线外啮合这一现象进行了描述，并分析了线外啮合对啮合刚度、静态传递误差，以及动态响应的影响。Lin等[13]提出了一种关于齿轮对接触冲击的有限元方法，完成了动静态接触分析。典型的啮合冲击主要包括啮入冲击和啮出冲击，Seireg等[14]通过试验验证了啮入冲击的影响明显比啮出冲击大，因此本文中主要考虑啮入冲击的影响。

通常，转速在3 000 r/min、线速度在22 m/s(AGMA规定3 600 r/min、25.4 m/s)以上的齿轮传动件被称为高速齿轮。随着工业发展，齿轮转速越来越高，载荷越来越大，齿轮减振降噪和修形技术虽然不断有所进展，但还是远远不能满足要求。例如高速航空齿轮，对其减振降噪始终有苛刻要求；舰船传动中，尤其是潜艇动力传动，其齿轮噪声水平远远落后于先进工业国家。因此，进一步研究齿轮修形和减振降噪技术仍然具有重要的现实意义。为此，本文提出一种考虑了重合度影响的齿面修形方法，和基于TCA和LTCA的啮入冲击力计算方法，并建立了以冲击力和ALTE为优化目标的优化模型，并通过智能优化算法，得到优化修形量，最终的计算结果显示，与传统修形方法相比，文中提出的考虑了重合度影响的新修形方法能够更有效的减小ALTE和啮入冲击力。

1 承载传动误差计算

通过TCA和LTCA可以得到接触线离散点位置坐标、接触线载荷密度，以及轮齿法向位移Z等[15-16]，其中将轮齿法向位移Z转化为啮合线上位移，并用转角表示即为承载传动误差(Loaded Transmission Error, LTE)。

LTE和ALTE可以表示如下：

(1)

式中：Te为承载传动误差；FALTE为承载传动误差波动幅值；rb、β分别为大轮基圆半径和螺旋角。

2 啮入冲击力的计算

2.1 啮入点位置的确定

啮入冲击力的计算关键在于准确求得啮入点的位置。齿轮修形后，接触区仅在部分齿面，此处以减速齿轮对为例进行说明。轮齿进入啮合时，实际啮入点并不是从大轮齿顶点开始，而是从齿面上某一点开始。本文中的啮入点位置的求解，综合考虑了齿面修形和轮齿负载变形的影响。在齿轮副负载传动中，由于轮齿变形，如图1(a)和(b)中所示，小轮齿对1对应的基节变小，大轮齿对1对应的基节变大，这会导致齿对2提前进入啮合。此时即将进入啮合的大轮轮齿的位置，可看作其在理论位置的基础上退回了一个微小角度，该角度可通过LTCA技术计算得到，而此时即将进入啮合的小轮齿面的瞬时接触点位置，可通过其齿面与上述大轮接触分析获得。图2给出了啮入冲击示意图。

1.负载1的LTE；2.负载2的LTE；3.负载3的LTE

(b) 新修形齿面实际啮入点求解

(c) 齿面实际啮入点示意图

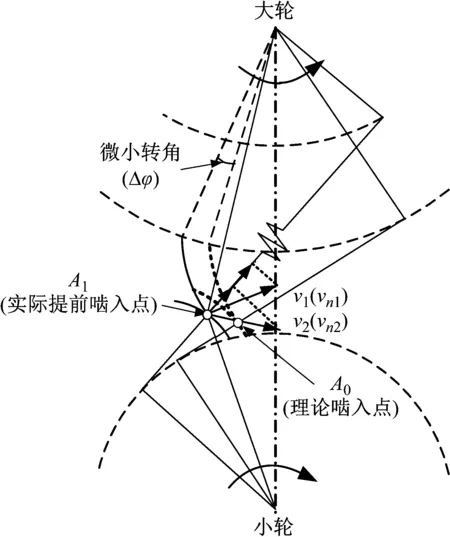
图2 啮入冲击示意图

通过TCA和LTCA技术，可以求得TE曲线和LTE曲线，如图1(a)和(b)中所示。图1(a)和(b)中，δ1为轮齿2在理论啮入位置处对应的TE，Δφ则为即将进入啮合的大轮轮齿在理论位置的基础上退回的微小角度。图1(c)中A0为理论啮入位置，A1为实际啮入位置。图1(b)中的新修形方法将在小节3中详细说明。

Δφ=Te-δ1

(2)

2.2 冲击力的计算

通过小节2.1可以准确计算初始啮入点的位置，再根据TCA和LTCA可以计算两齿面在该点的相对法向速度和啮合刚度。

啮合齿轮对的转动惯量为：

(3)

将两啮合齿轮的转动惯量转化为瞬时啮合线上的诱导质量：

(4)

式(3)和(4)中：J1和J2分别为小轮和大轮的瞬时转动惯量；b为齿宽；ρ为齿轮材料密度；rh1和rh2分别为两齿轮轮毂内孔半径；rb1和rb2分别为大小轮的基圆半径。

齿轮副啮入冲击点的冲击动能为：

(5)

式中：vs为大小轮齿面在初始接触点的相对法向速度。

由于冲击作用，使得轮齿之间产生冲击变形量δs，与之相对应的冲击力Fs则为最大冲击力。根据冲击力学理论[17]，冲击动能Ek、最大变形δs以及最大冲击力Fs之间有如下关系：

(6)

最终得到初始啮入冲击点的啮入冲击力表达式：

(7)

式中：Ks为大小轮齿面在初始接触点的啮合刚度。

3 修形齿面的构造和齿面优化修形

在文献[4]中，作者对内啮合人字齿轮对中的小轮进行了三维修形，本文中，将文献[4]中的修形齿面构造方法应用在外啮合斜齿轮对中。

图3(a)为新修形方法中设定的齿廓修形曲线。由于篇幅所限，此处的新齿廓修形曲线的基本形状设定方法，以重合度处于2和3之间的齿轮对为例来说明。对于重合度处于2和3之间的齿轮对，轮齿从进入啮合到退出啮合，需要经历“三齿-两齿-三齿-两齿-三齿”的啮合过程，在多数情况下，三齿啮合区的轮齿负载变形小于两齿啮合区的负载变形，LTE呈现波动趋势。为了跟踪这种波动趋势，实现补偿LTE的目的，本文中的新修形将齿廓修形曲线设定为一六阶抛物线。而当齿轮重合度更大时，比如重合度处于3和4之间，则需要更高阶的曲线，来获得双内凹的修形曲线，来跟踪更为频繁的齿轮对数交替变化。

y=a0+a1x+a2x2+a3x3+a4x4+a5x5+a6x6

(8)

(9)

图3(b)和(c)分别为传统的中凸齿廓和齿向修形曲线，都由两段四阶抛物线和一段直线组成。其中，y1和y2分别为齿根和齿顶的最大修形量；y3和y4分别为齿根和齿顶的修形长度；y5为齿向两端最大修形量；y6为齿向不修形区域长度；H和B分别为有效齿高和齿长。

通过以上说明，可以发现，新修形方法和传统中凸修形方法的主要区别在于齿廓修形曲线的不同。在新修形方法中，齿廓修形曲线为高阶修形曲线，如图3(a)中所示。而在传统修形方法中，齿廓修形曲线由两段四阶抛物线和一段直线组成，如图3(b)中所示。而对于齿向修形，新方法和传统方法一样，都为中凸修形，如图3(c)所示。这是因为，齿向修形主要是用于减小误差敏感性的，在这一方面，新修形和传统修形是类似的。图3(a)中的齿廓修形和图3(c)中的齿向修形相结合，即为新三维修形。图3(b)中的齿廓修形和图3(c)中的齿向修形相结合, 即为传统三维修形。

(a) 高阶齿廓修形曲线(新修形)

(b) 四阶齿廓修形(传统修形)

(c) 四阶齿向修形(新修形和传统修形)

当对齿面进行优化修形时，优化模型可表示为：

优化变量(新修形)：δ1、δ3、δ5、λ1、λ2、y5、y6

优化变量(传统修形)：y1、y2、y3、y4、y5、y6

目标函数：

(10)

约束条件(新修形)：

(11a)

约束条件(传统修形)：

(11b)

式中：本文算例δmin1、δmax1、δmin2、δmax2分别取为5 μm、30 μm、0.5 μm、5 μm，λmin和λmax分别取为0.2和0.8，lmin和lmax分别取为5 mm、70 mm，hmin和hmax分别取为0.5 mm、5.5 mm。

传统的多目标优化方法是将多目标乘以权重再线性相加，转化成单目标优化问题求解，往往存在主观性强、局部最优、各目标相互制约等缺点。因此，本文中采用带有精英策略的快速非支配排序遗传算法(NSGA-II)[18]，该算法采用快速非支配排序算法和拥挤距离比较算子，引入精英策略，降低了计算复杂度，适用于非线性多目标优化问题。

下面的算例中，遗传算法的种群个数设为100，进化代数设为50。

图4 齿面修形优化计算流程图

4 算例与分析

本文中只对小轮修形。图中的δφ2A为承载传动误差波动幅值，δφ2为承载传动误差，φ1为小轮转角。

表1 齿轮副参数

图5中给出了齿面基于传统修形方法和新修形方法的优化修形量。齿轮在啮合过程中，轮齿从进入啮合到退出啮合需要经历“三齿-两齿-三齿-两齿-三齿”的啮合过程。如图中所示，传统修形方法未考虑轮齿啮合过程中，齿轮对数交替转换的影响，因此只在齿顶、齿根以及齿向两侧区域进行修形，而在新修形方法中，考虑了这一影响，因此在齿面中间区域也有少量的修形，这将有助于提高齿轮的啮合性能。图6中给出了未修形齿面、传统修形齿面，以及新修形齿面的ALTE对比。从图6(a)可以发现，新修形方法比传统修形方法显然更能够有效的减低ALTE，基于新修形方法，齿面修形后，ALTE下降百分比为69.7%，基于传统修形方法，齿面修形后，ALTE下降百分比为28.1%。图6(b)中给出了ALTE随负载的变化，从图中结果可以看出，新修形不仅仅在预设负载1 200 Nm时的ALTE最小，而且在一定的负载范围内，其ALTE都比传统修形要小，此外，也可以发现，负载从1 000 Nm增大到1 200 Nm时，随着负载增大，ALTE呈下降趋势，在预设负载下，ALTE达到最小，然后，ALTE随负载增大而随之增大，这是因为在新修形方法中，考虑了重合度的影响，因此，新修形能够准确的跟踪轮齿啮合过程中的轮齿负载变形趋势，能够对其进行更有效的补偿。

(a) 传统修形

(b) 新修形

1.传统修形：1.64;2.新修形:0.69;3.未修形：2.28

(b) ALTE随负载的变化波动

图7中给出了未修形齿面、传统修形齿面和新修形齿面的TE，以及多载荷下的LTE。图中的结果主要是为了获得啮入冲击力计算中需要的微小滞后角度Δφ。Δφ越大，则啮入点的相对速度越大。图7(a)中为未修形齿面的TE和LTE，从图中可以看到，未修形齿面的TE几乎为零，LTE随负载增大而增大，LTE反映的是轮齿变形，负载越大，轮齿变形越大，由于未修形齿面没有TE对其进行补偿，因此，负载越大，被动轮滞后角度越大。图7(b)中为传统中凸修形齿面的TE和LTE，从图中可以看出，由于传统中凸齿面只在轮齿边缘区域进行修形，因此，后一对轮齿的TE很难对前一对轮齿的负载滞后进行有效补偿。图7(c)中为考虑了齿轮重合度的新修形齿面的TE和LTE，从图中可以看出，TE中的中凹部分有效的补偿了前一对轮齿的负载滞后，这将有助于减小啮入冲击速度，进而减小啮入冲击力。

(b) 传统修形齿面ALTE随负载的变化

(c) 新修形齿面ALTE随负载的变化

图8中给出了冲击速度、冲击刚度和冲击力随负载的变化趋势。从图8(a)中可以看出，冲击速度随负载的增大而增大。负载越大，轮齿的变形越大，后一对轮齿进入啮合时的基节误差也越大，因此，在接触点的相对速度也越大。图8(b)给出了啮入接触点刚度随负载的变化趋势。齿面修形后，后一对轮齿进入啮合时，随着负载增大，接触点在小轮齿面上是往齿根方向移动的，在大轮齿面上是往齿顶方向移动的，直到达到大轮的齿顶点。因此，在这一过程中，修形齿面随着负载增大，初次接触点刚度是随着负载增大而减小的。而对于未修形齿面，无论怎样，后一对轮齿进入啮合时，总是从大轮的齿顶点开始的，随着负载增大，基节误差越大，后一对轮齿进入啮合时的初始接触点位置，在小轮齿面上是从齿根往节线方向移动的，因此，未修形齿面的初始接触点刚度是随着负载增大而增大的。图8(c)给出了啮入冲击力随负载的变化趋势。对比图8(a)可以发现冲击力随负载的变化趋势与冲击速度随负载的变化趋势是一致的，都是随着负载增大而增大的，从图中的曲线变化趋势，可以发现，冲击速度对冲击力的影响，显然要比刚度对冲击力的影响要大。

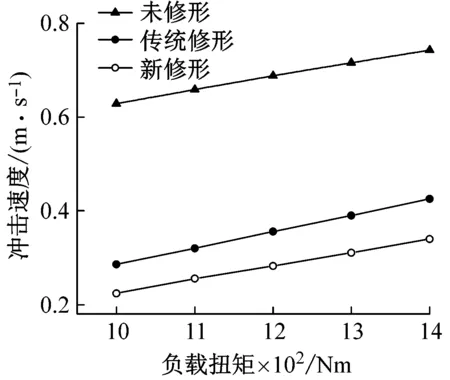
(a) 冲击速度随负载的变化波动

(b) 冲击刚度随负载的变化波动

(c) 冲击力随负载的变化波动对比

图9给出了啮入冲击速度和冲击力随小轮转速的变化趋势，从图中可以看出，随着小轮转速增大，冲击速度和冲击力呈线性增大趋势。因此，尤其是高速齿轮，降低啮入冲击力，对其减振降噪是极其有意义的。同时可以看到，新修形齿面在啮入点的冲击速度比传统修形齿面的要小，这是因为，新修形齿面的内凹部分有效减弱了前一对啮合轮齿的负载变形对后一对即将进入啮合的齿轮对的影响。同时从图8(b)可以看出，传统修形齿面和新修形齿面在啮入点的刚度差别并不是很明显。因此，相比于传统修形齿面，新修形齿面的啮入冲击力大大降低。新修形除了能更有效的降低ALTE，也可以更有效的降低啮入冲击力。

(a) 冲击速度随小轮转速的变化

(b) 冲击力随小轮转速的变化

Fig.9 Variations of the mesh-in impact force with pinion rotation velocity, the output load is 1 200 Nm

5 结 论

承载传动误差波动和啮入冲击力是齿轮传动中噪音和振动的主要激励源。啮入冲击力受齿轮转速影响较大，降低啮入冲击力对高速齿轮减振降噪是极其有意义的。根据文中的分析，可以得到以下结论：

(1) 齿轮转动过程中，轮齿从进入啮合到退出啮合，相接触的轮齿对数是交替转换的。文中提出的新修形方法，考虑了这一因素的影响，能够更精确的跟踪轮齿负载变形的趋势，因此，更有效的降低了ALTE。

(2) 新修形方法在预设优化负载下，以及预设负载附近的一定负载范围内，都能够更有效的降低ALTE。

(3) 文中提出的啮入冲击力计算方法考虑了齿面修形和轮齿负载变形的影响，可以较准确的计算未修形齿面和修形齿面的啮入冲击位置，进而可以较准确的得到啮入冲击力。

(4) 新修形齿面减小了由于轮齿负载变形而引起的基节偏差的影响，从而减小了在轮齿进入啮合的初始接触点处的相对速度，因此，啮入冲击力比传统修形齿面要小。

(5) 现代加工制造技术的提高为新设计的实现提供了一定保障，本文提出的新修形方法为高速齿轮减振降噪提供了一条新的途径。