主动转动惯量驱动控制系统对多类型灾害源激励悬吊结构摆振响应控制研究

张春巍，王 昊

(青岛理工大学 土木工程学院，山东 青岛 266033)

传统的防灾设计中，通常都是将各种灾害效应分开考虑，单独进行设计，或者仅考虑结构物在地震作用下的防灾设计，忽视了结构物面对多种灾害的综合需求[1-3]。动力多灾害作用，往往比单一灾害更为复杂，其破坏性也更为严重。在地震、火灾、风灾、爆炸、冲击等单一灾害来源的工程结构性能与设计方面，相关研究领域已经取得了丰富的成果，但如何提高工程结构在动力多灾害作用下的抗灾能力和可恢复性，降低其损伤，减轻灾害损失，目前仍鲜有研究。多灾害的概念包含但不限于对“灾害组合”的考虑。由于各种灾害的性质、发生概率、后果、结构抗灾对策与设计理念都存在很大差别，通常而言，“多灾害”主要包含多种单一灾害如在设计中考虑结构对地震、海浪冲击、强风等多种灾害单一作用效应，以及可能同时或时间上前后连续发生的不同灾害的组合，如地震与海啸、强风与海浪等2种及以上灾害同时或连续作用[4-5]。

悬吊结构的摆振是一种典型且常见的运动形式，根据吊点与结构运动方向的关系主要分为3种运动形式：平动悬吊模式、转动悬吊模式以及平动与转动耦合悬吊模式。大量的研究和实践证明，常见的振动控制装置，如调谐质量阻尼器TMD(Tuned Mass Damper)、主动质量阻尼器AMD(Active Mass Damper)，在控制结构的平动方面具有良好的控制效果[6-12]。对于悬吊结构的振动控制问题，TMD、AMD等传统的控制装置在平动悬吊模式的摆振控制中控制效果较好，但是在转动悬吊模式的摆振控制中基本无效[13]。

另外，此前的研究都是基于常见单一工况下的性能试验，验证控制系统的性能，该方法由于注重系统自身构造的设计而容易忽视外部荷载对结构性能的影响，无法全面评价控制系统的性能。如，TRID控制系统在某种频率正弦激励下可以发挥出较好的控制作用，而在不同类型单一灾害源激励结构的控制效果，如地震动输入、海洋波浪激励，尚没有进行系统深入的研究。

本文基于文献中的TRID控制系统的概念，提出了主动转动惯量驱动控制系统(Active Rotary Inertia Driver,ARID)概念，建立了ARID系统在悬吊结构吊点激励作用下系统的简化分析模型，本文针对ARID系统，考虑多类型灾害源激励结构的单一灾害振动控制机理，通过理论分析、数值模拟以及振动台模型试验，系统全面研究ARID系统在悬吊结构多类型灾害源激励结构摆振响应的控制方案及其控制性能，从机理上证明ARID系统对多类型灾害源激励结构摆振响应控制应用的可行性。

1 悬吊结构——ARID系统简化分析模型

建立如图1所示的ARID系统简化分析模型，该结构体系有2个自由度：悬吊结构的摆动角度θ、ARID系统的驱动装置驱动转动惯量圆盘相对地面的转角φ。图1中l为悬吊结构的摆长，m为悬吊质点的质量，ma为转动惯量圆盘的质量，Ja为ARID系统转动惯量圆盘的转动惯量，c为悬吊结构体系的阻尼系数，ca为ARID系统的阻尼系数，ka为ARID系统的转动刚度系数,ax0(t)为吊点处激励的加速度，Ma(t)为ARID系统的输出转矩。该体系的运动方程：

(1)

(2)

式(2)中包含ARID系统的阻尼力、抗扭转力以及输出主动控制力，通常情况下，驱动装置选用为直流伺服电机时，其阻尼力和抗扭转力与其他作用力相比非常小，可以忽略不计。

图1 悬吊结构及其摆振控制ARID系统简化分析模型

Fig.1 Simplified analysis model of suspended structure with the ARID system

本文设定顺时针摆动为正，假定悬吊结构在小于正负90°的范围内摆动，令sinθ≈θ,cosθ≈1，可将体系原非线性运动方程线性化为：

(3)

(4)

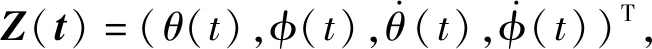
成果表包括界桩登记表、三交点界桩登记表、界桩成果表、界址点成果表、三交点成果表和界线协议书附图备考表。参考1998年陕西省各乡镇联合勘界相关成果，对边界线上的界线名称、边界点名称、编号、坐标及行政归属等内容形成不同制式表格模板，方便信息录入、管理与查询。

2 ARID系统摆振控制的振动台模型试验

2.1 试验系统概念设计

基于上述简化分析模型、运动方程及控制算法，设计了控制系统的主动控制概念关系如图2所示。为了保证控制效果，整个系统采用闭环控制，控制系统可以根据结构实时响应及时调整控制力输出的大小。采用单轴振动台作为激励装置，在以上闭环控制概念的基础上，还需要设计结构响应的数据采集装置、出力装置以及相应的控制器。设计如图3(a)所示的试验系统，摆角即为结构的响应，选取光电编码器与结构吊端固定连接，结构带动光电编码器转轴转动即可采集结构的摆角。如图3(b)所示为出力装置设计原理图，出力装置选用直流伺服电机，驱动转动惯量圆盘发生回转转动，从而产生作用于结构的控制力。控制器选用计算机和功放，根据结构的响应控制电机驱动转动惯量圆盘回转运动。

图2 ARID系统主动控制概念关系图

2.2 多种工况振动台试验系统

基于前期针对AMD的研究和试验系统的概念设计，悬吊结构ARID系统试验采用Quanser单轴振动台及配套的硬件/软件，驱动器选用Maxon公司生产的直流电机及行星减速箱。分别选用US Digital公司和Maxon公司生产的光电编码器测量结构摆角和转动惯量圆盘的转角，采样分辨率分别为0.087 9°和0.18°。如图4(a)所示，结构悬吊端安装在光电编码器转轴上，通过光电编码器实时测量结构的摆角；另外一个光电编码器安装在驱动器上，其转轴与驱动器同轴转动。Quanser Shake TableⅡ为单轴小型振动台，最大加速度为2.5 g，两侧最大行程为7.5 cm，最大使用频率为10 Hz，达到最大加速度时，最大可承载质量为7.5 kg。电机主要参数为：额定电压24 V，空载转速8 810 r/min，额定转速8 050 r/min，额定转矩85.6 mN·m，堵转转矩1 020 mN·m，转子转动惯量33.5 g·mm2；行星减速箱主要参数为：减速比3.7∶1，最大连续扭矩为0.75 Nm，转动惯量1.5 g·mm2。

(a)振动台试验系统图(b)ARID设计原理图

图3 ARID悬吊结构振动台试验系统简图

Fig.3 Sketch diagram of the ARID suspended structure shaking-table experimental system

3 振动台试验结果与数值模拟对比分析

共设计了5种工况振动台模拟试验，分别是：正弦激励输入下结构自由衰减振动、正弦激励输入下结构强迫振动、正弦扫频激励、模拟地震动El Centro地震波输入、模拟海洋波浪激励。每种工况进行ARID控制系统开启和关闭两种状态下的对比试验。同时，利用MATLAB/Simulink建模，进行基于多类型灾害源激励结构振动台试验的数值模拟。

(b) 悬吊结构试验构造图

(c) 出力装置照片

图4 ARID振动台试验系统图

Fig.4 The ARID shaking table experimental system

3.1 正弦激励输入下结构自由衰减振动

试验实施方式如下：共计采集数据时间为40 s，输入振动台正弦激励波形，幅值20 mm，频率0.65 Hz，激励时间为15 s。采样时间内，前15 s ARID处于关闭状态，第15 s时刻振动台停止运行，ARID开机运行或依然保持关机，直至40 s，采样结束。对比采样时间段内，15 s之后开启ARID控制系统与否的试验结果。试验与数值模拟对比结果,如图5所示。

(a) 试验摆角时程曲线

(b) 数值模拟摆角时程曲线

(c) 无控状态试验模拟摆角时程曲线对比

(d) 有控状态试验模拟摆角时程曲线对比

(e) 频域对比分析曲线

图5 正弦激励输入下结构自由衰减振动结果

Fig.5 The results of free decay of structural response under sinusoidal excitation

3.2 正弦激励输入下结构强迫振动

试验实施方式：输入振动台正弦激励波形，幅值为20 mm，频率为0.65 Hz。保持ARID系统关闭，设置振动台运行80 s；保持ARID开启，设置振动台运行80 s。采集摆角，对比ARID开启与否的试验结果。试验与数值模拟对比结果,如图6所示。

(a) 试验摆角时程曲线

(b) 数值模拟摆角时程曲线

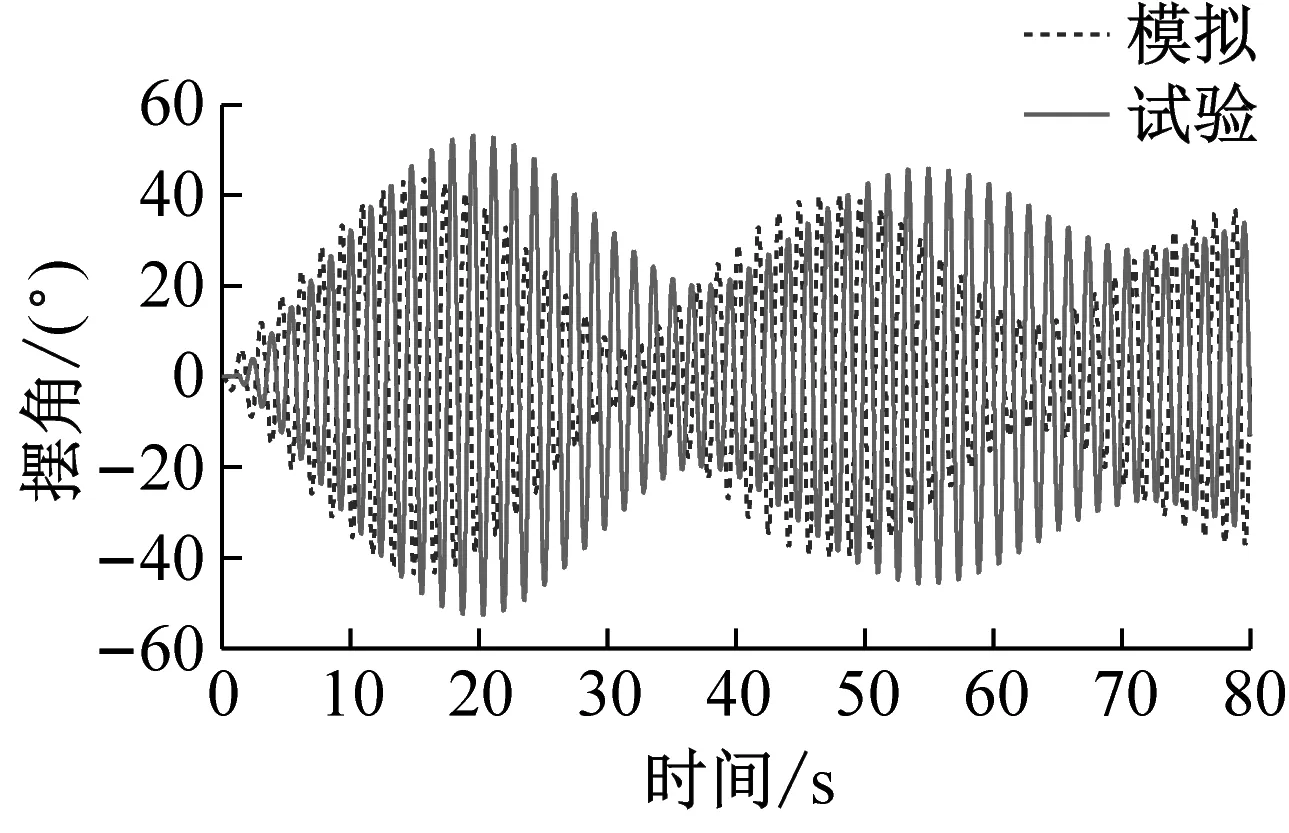
(c) 无控状态试验模拟摆角时程曲线对比

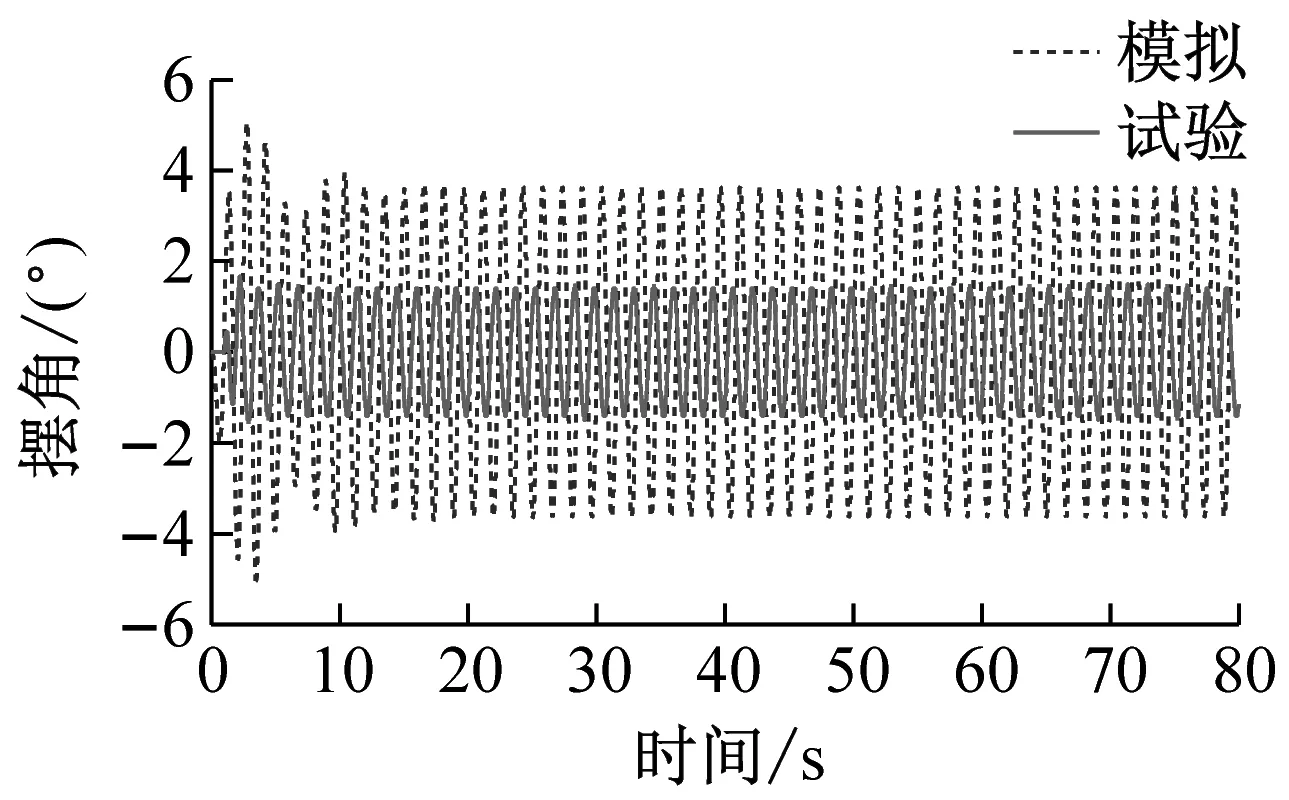
(d) 有控状态试验模拟摆角时程曲线对比

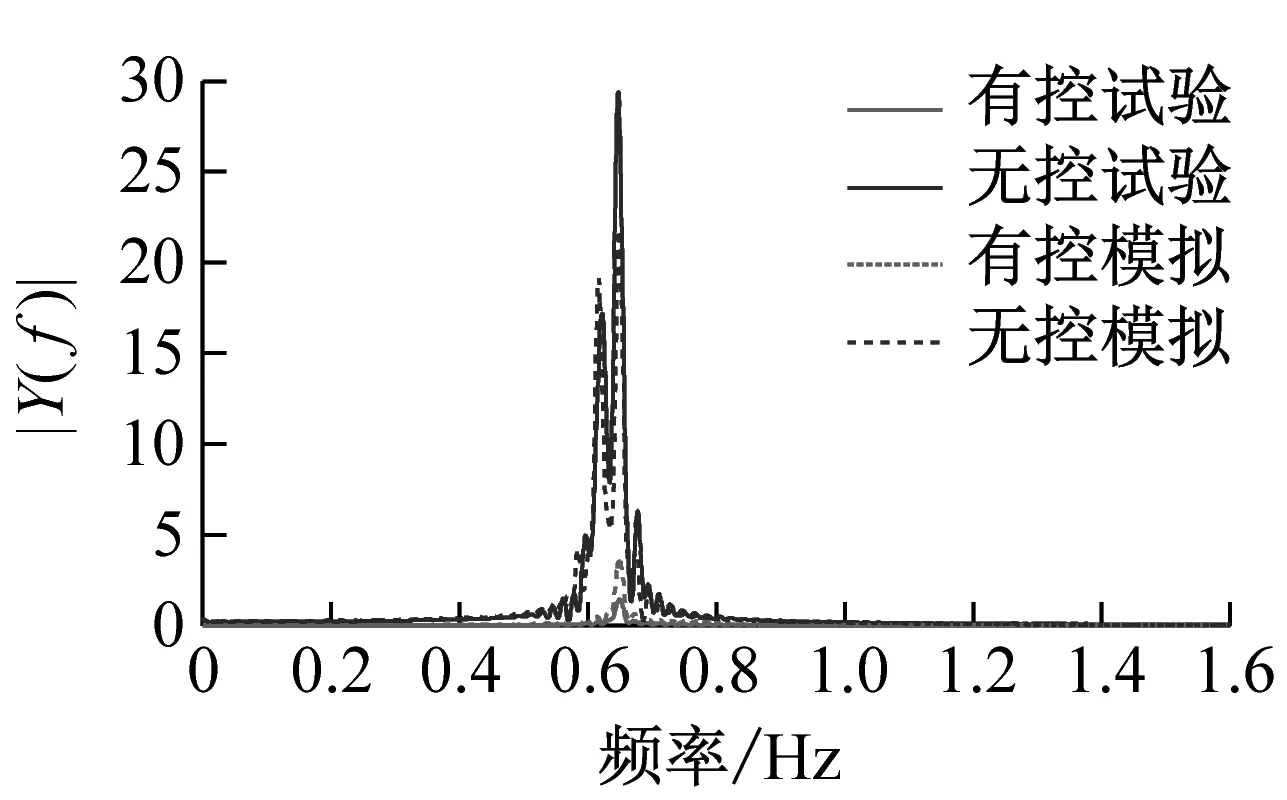
(e) 频域对比分析曲线

图6 正弦激励输入下结构强迫振动结果

Fig.6 The results of forced vibration of structural response under sinusoid excitation

3.3 正弦扫频激励

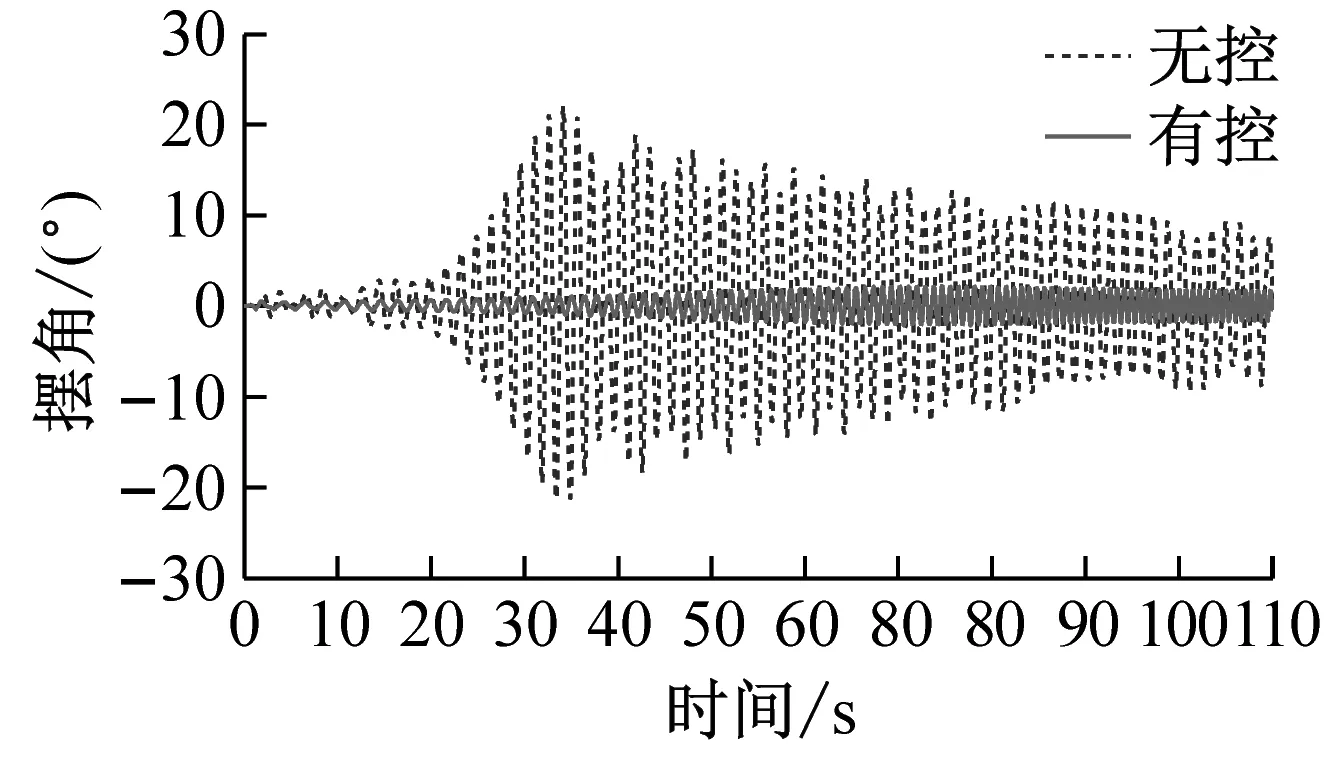
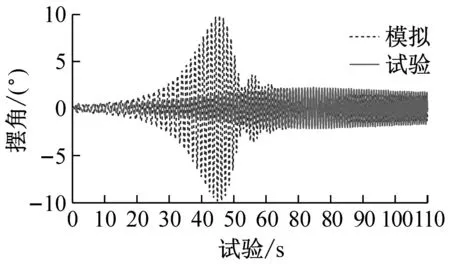
试验实施方式：输入振动台幅值为10 mm，初始频率0.4 Hz，结束频率1.5 Hz，总时间110 s的扫频波形，进行ARID开启与关闭状态下的试验，对比试验结果。试验与数值模拟对比结果,如图7所示。

(a) 试验摆角时程曲线

(b) 数值模拟摆角时程曲线

(c) 无控状态试验模拟摆角时程曲线对比

(d) 有控状态试验模拟摆角时程曲线对比

(e) 频域对比分析曲线

图7 正弦扫频激励结果

Fig.7 The results of structural response under sinusoidal sweep excitation

3.4 模拟地震动El Centro地震波输入

试验实施方式：输入模拟地震动波形为El Centro地震波，采样总时长为40 s，进行ARID开启与关闭状态下的试验，对比试验结果。试验与数值模拟对比结果,如图8所示。

(a) 试验摆角时程曲线

(b) 数值模拟摆角时程曲线

(c) 无控状态试验模拟摆角时程曲线对比

(d) 有控状态试验模拟摆角时程曲线对比

(e) 频域对比分析曲线

图8 模拟地震动El Centro地震波输入结果

Fig.8 The results of structural response under El Centro seismic excitation

3.5 模拟海洋波浪输入

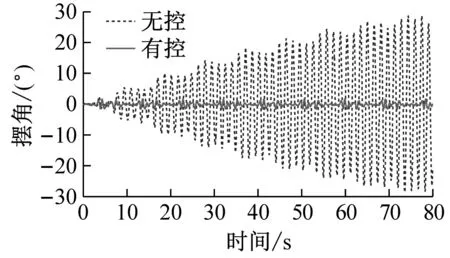
试验方式为：选取高斯平稳白噪声作为加速度信号，通过处理生成随机海浪波谱输入振动台，模拟海洋波浪荷载进行ARID开启与关闭状态下的试验，对比试验结果。试验与数值模拟对比结果,如图9所示。

(a) 试验摆角时程曲线

(b) 数值模拟摆角时程曲线

(c) 无控状态试验模拟摆角时程曲线对比

(d) 有控状态试验模拟摆角时程曲线对比

(e) 频域对比分析曲线

图9 模拟海洋波浪输入结构结果

Fig.9 The results of structural response under ocean wave excitation

3.6 试验与数值模拟结果对比分析

根据以上试验结果以及基于试验的数值模拟结果，可以发现试验结果与数值模拟结果吻合较好，无控模拟结果与试验结果的吻合性优于有控，ARID控制系统均表现出了较好的控制效果。试验与模拟结果对比发现，试验得到的时程曲线比模拟结果有微小的时间延后现象，这是振动台启动时的时间滞后造成的。正弦激励输入下结构自由衰减振动工况，在系统开启后，悬吊结构摆角很快消减，控制效果明显；正弦激励输入下结构强迫振动工况，有控状态时，控制系统将摆动控制在很小的范围内且保持稳定，控制系统起到了相当于“过滤”激励的作用；正弦扫频激励工况，控制系统将结构摆动控制在较小的范围内，随着激励频率的变化，摆动幅值有较小的波动；模拟地震动El Centro地震波输入和模拟海洋波浪激励工况，控制系统同样可以将结构摆动控制在很小的范围内，当外部激励加速度发生突变时，摆动会有“突变”，但控制系统依然可以将“突变”控制在较小的范围内，同样起到了“过滤”激励的作用，控制效果明显。各种工况结果比较如表1所示。

峰值衰减率Peak值代表了ARID控制系统对摆角峰值的控制效果，均方根值衰减率RMS值代表了ARID系统对摆角摆幅离散程度的控制效果。定义两项指标峰值衰减率(Peak)和均方根值衰减率(RMS)如下：

如表1所示，ARID系统在不同工况下的控制效果非常明显，均大大减小了结构的最大摆角，试验表明，ARID系统可以使结构摆角减小90%以上；另外，保持ARID系统开启，当结构无初始摆角时，受到正弦、正弦扫频、模拟地震动、模拟海浪激励作用，结构摆角被控制在10°以内，可以看出ARID系统具有很好的控制性能。

表1 试验与模拟结果对比表

4 结 论

本文针对所提出的主动转动惯量驱动控制系统(ARID)，设计了验证ARID系统性能的多工况振动台试验，并进行基于多工况振动台试验的Simulink模拟仿真。通过试验结果和模拟仿真结果，得到以下结论：

(1) ARID系统多类型工况下振动台试验，通过对结构模型施加不同类型的激励作用，研究ARID系统在多类型灾害源激励结构摆振响应控制的有效性。试验结果表明，ARID系统在不同工况下均表现出了良好的控制效果，对悬吊结构摆振响应控制具有有效性。

(2) 通过利用Simulink进行基于振动台试验的ARID系统模拟仿真，仿真结果与试验结果吻合较好，验证了试验的可靠性。另外，进一步证明了ARID系统在悬吊结构多类型灾害源激励结构摆振响应控制的有效性。

(3) 结构在无初始摆角的条件下，受到外部激励作用时，ARID系统可以将结构摆角控制在很小的范围内，作用效果受外部激励的影响作用较小，起到了“过滤”激励的作用，从而验证了主动控制ARID控制系统闭环控制，受外界干扰小、性能好的优越性。

综合考虑ARID控制系统的模型试验和模拟结果可以发现，ARID系统可以在多灾害源激励作用下均表现出良好的控制效果，验证了ARID系统的稳定性和鲁棒性，从机理上证明了该系统对多类型灾害源激励结构摆振响应控制应用的可行性，对今后多类型灾害下的防灾设计具有重要意义。