预警机典型巡逻航线下探测性能分析及评估

单博楠,傅宇龙,叶海军,乔永杰

(中国电子科学研究院，北京 100041)

0 引 言

预警机被誉为现代战场的“空中帅府”，担负着低空补盲、机动预警、指挥控制、战场管理等重要作用，是现代战争空中预警探测和指挥控制的核心节点[1-2]。在遂行作战任务过程中，预警机通常采用在巡逻空域内绕巡逻航线飞行的活动方式。预警机巡逻空域的设置通常要有利于作战思想和作战意图、有利于预警机发挥预警探测能力、有利于通信联系、有利于护航编队护航等。限制因素有预警雷达探测范围、预警机最大续航时间、通信传输距离、我方护航或庇护范围、敌方可能来袭方向、敌方防空火力范围等。然而在预警机航线规划[3-4]和巡逻空域设置的文献[5-6]中，鲜少考虑巡逻航线形状和大小对预警探测能力的影响。

预警机巡逻航线的形状和大小与巡逻空域大小、巡逻航时长短、预警探测强效区面积和径向速度盲区相互影响相互制约，是预警机作战使用与任务规划中必须要考虑和分析的。因此本文对预警机四种典型巡逻航线进行了分析和对比。本文首先对预警机四种典型巡逻航线，跑道形、8字形、三角形和圆形航线进行建模。其次建立预警机预警探测的总覆盖区、弱效区和强效区数学模型。最后从巡逻空域大小、巡逻航线周长、强效区面积和径向速度盲区四个方面对比四种典型巡逻航线，并给出航线选择建议。

1 预警机典型巡逻航线建模

预警机常用的四种巡航航线分别为跑道形航线、8字形航线、三角形航线和圆形航线，如图1所示。本文在直角坐标系内对四种典型航线建立数学模型。定义航线的活动空域为航线几何图形的外接矩形(三角形航线的活动空域认为是三角形外接圆的外切正方形，圆形航线的活动空域认为是圆形的外切正方形)。定义航线的周长为几何图形的周长。

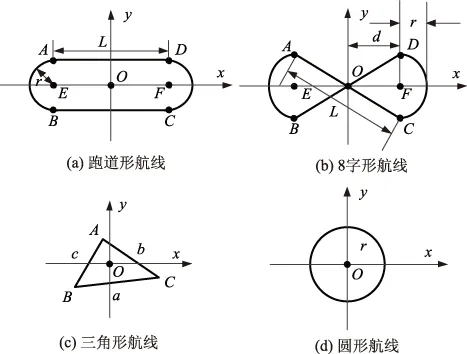
图1 预警机常用的四种巡航航线

1.1 跑道形航线

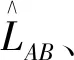
(x+L/2)2+y2=r2,-L/2-r≤x≤-L/2

(1)

y=-r,-L/2≤x≤L/2

(2)

(x-L/2)2+y2=r2,L/2≤x≤L/2+r

(3)

y=r,-L/2≤x≤L/2

(4)

跑道形航线的活动空域为：A=(L+2r)×2r。

跑道形航线的周长为：C=2L+2πr。

1.2 8字形航线

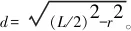
(x+d)2+y2=r2,-d-r≤x≤-d

(5)

(6)

(x-d)2+y2=r2,d≤x≤d+r

(7)

(8)

8字形航线的活动空域为：A=(2d+2r)×2r。

8字形航线的周长为：C=2L+2πr。

1.3 三角形航线

(9)

(10)

(11)

三角形航线的活动空域为：A=2r×2r。

1.4 圆形航线

如图1(d)所示，以圆心为原点，以r为转弯半径的圆形航线的方程为：

x2+y2=r2,-r≤x≤r

(12)

圆形航线的活动空域为：A=2r×2r。

圆形航线的周长为：C=2πr。

2 预警探测的总覆盖区、弱效区和强效区建模

预警机预警探测的总覆盖区、弱效区和强效区的定义[7]如下：

定义1：预警机巡逻探测总覆盖区是指预警机沿着航线巡逻时，所能探测到的区域总和。

定义2：预警机巡逻探测强效区是指预警机沿着航线巡逻时，在巡逻航线上的任意位置点都能够探测到的区域。

定义3：预警机巡逻探测弱效区是指预警机沿着航线巡逻时，在巡逻航线上的有些位置点可以探测到，有些位置点探测不到的区域。

假设预警机在空中不动时的探测范围为以预警机所在位置为圆心、以雷达最大探测距离Rm为半径的一个圆(暂不考虑盲区)，当预警机沿巡逻航线飞行时，这个探测圆就随之一起运动。根据上述定义，强效区可以转化为如下数学模型进行求解：即以巡逻航线上的各位置点为圆心、以载机雷达最大探测距离Rm为半径的所有圆的交集。总覆盖区即所有圆的并集。弱效区则是并集减去交集(即对称差集)。四种典型巡逻航线对应的预警探测总覆盖区、弱效区和强效区的示意图如图2所示。

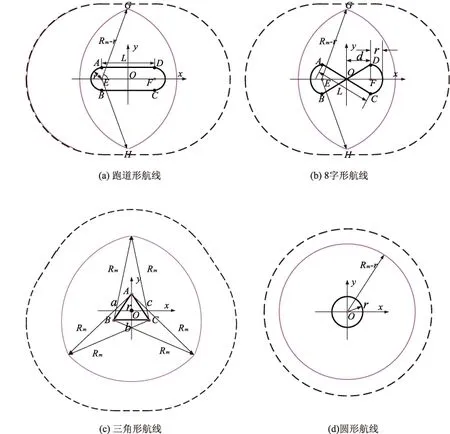
图2 四种典型巡逻航线的预警探测总覆盖区、弱效区和强效区示意图

2.1 跑道形航线

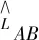
-L/2-r≤x≤-L/2

(13)

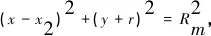
-L/2≤x2≤L/2

(14)

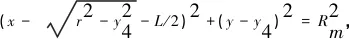
L/2≤x≤L/2+r

(15)

(16)

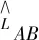
S总覆盖区=π(Rm+r)2+2(Rm+r)L

(17)

总覆盖区的包络即弱效区的包络，如图2(a)中灰色虚线所示，方程为：

(18)

(19)

强效区包络的方程为以E为原点、以Rm-r为半径的圆和以F为原点、以Rm-r为半径的圆的交集，两个圆的交点为G和H，其中∠GEF=∠HEF=arccos(L/(2×(Rm-r)))，如图2(a)中紫色实线所示，强效区包络方程为：

(20)

2.2 8字形航线

预警机沿着8字形航线巡逻时，总覆盖区的面积S总覆盖区面积为：

S总覆盖区=π(Rm+r)2+4(Rm+r)d

(21)

总覆盖区的包络即弱效区的包络，如图2(b)中灰色虚线所示，方程为：

(22)

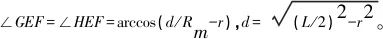
(23)

预警机探测强效区的面积为：

(24)

2.3 三角形航线

预警机按照三角形航线巡航时，总探测区为以三角形顶点A、B和C为圆心，以探测半径Rm为半径的三个圆的并集。总探测区面积为S=SA∪SB∪SC。强效区为以三角形顶点A、B和C为圆心，以探测半径Rm为半径的三个圆的交集。强效区面积为S=SA∩SB∩SC。

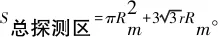
2.4 圆形航线

预警机按照圆形航线巡逻时，探测总覆盖区即弱效区包线方程为以航线圆心O为圆心，以探测距离家转弯半径，即Rm+r为半径的圆，如图2(d)中灰色虚线所示。总覆盖区面积为S总覆盖区=π(Rm+r)2。强效区为以航线圆心O为圆心，以探测距离减去转弯半径，即Rm-r为半径的圆，如图2(d)中紫色实线所示。强效区面积为S强效区=π(Rm-r)2。

3 预警机四种典型巡逻航线对比

3.1 活动空域受限时四种航线的强效区对比

预警机在作战使用中，往往是要在有限的活动空域中完成预警探测与指挥控制任务，因此本节对比在活动空域受限，即活动空域面积一定的情况下，四种航线的周长和强效区面积。认为强效区面积越大越好，周长越短越好。将四种航线两两对比。

3.1.1 对比跑道形与8字形航线

当跑道形和8字形航线活动空域相同时，即r跑道=r8字形，L跑道/2=d8字形。

结论1：当跑道形和8字形航线活动空域相同时，8字形航线平飞航线更长，航线周长更长。

结论2：当跑道形和8字形航线活动空域相同时，跑道形航线强效区与8字形航线强效区完全重合。

综上，当活动空域受限时，跑道形航线优于8字形航线。

3.1.2对比跑道形与圆形航线

圆形航线可以认为是一种特殊的跑道形航线，即L=0。对比转弯半径相同的跑道形航线和圆形航线，即r跑道=r圆形，L跑道>0。跑道形航线强效区面积公式是以L为变量的单调递减函数，当L=0时，即圆形航线时，取得最大值。

结论1：当跑道形航线的转弯半径相同时，圆形航线所需活动空域更小。

结论2：当跑道形航线的转弯半径相同时，圆形航线周长更短。

结论3：当跑道形航线的转弯半径相同时，圆形航线强效区面积更大。

综上，当活动空域受限时，圆形航线优于跑道形航线。

3.1.3对比8字形与圆形航线

8字形和圆形航线的对比与跑道形航线和圆形航线的对比相似。当8字形航线的长边等于两倍转弯半径时，即L8字形=2r8字形时，8字形航线成为一种特殊的圆形航线，但是考虑到此时飞行难度大，因此不考虑L8字形≤2r8字形的8字形航线。对比转弯半径相同的8字形航线和圆形航线，即r8字形=r圆形，L8字形>2r8字形。8字形航线强效区面积公式是以d为变量的单调递减函数，当d=0时，取得最大值。

结论1：当8字形航线的转弯半径相同时，圆形航线所需活动空域更小。

结论2：当8字形航线的转弯半径相同时，圆形航线周长更短。

结论3：当8字形航线的转弯半径相同时，圆形航线强效区面积更大。

综上，活动空域受限时，圆形航线优于8字形航线。

3.1.4对比三角形与圆形航线

三角形航线的活动空域定义是三角形的外接圆的外切正方形，圆形航线的活动空域是圆形的外接正方形，为简便，对比三角形外接圆和圆形航线即可。

结论1：当三角形航线与圆形航线的活动空域相同时，三角形航线的航线周长更短。

结论2：当三角形航线与圆形航线的活动空域相同时，三角形航线强效区面积更大。

综上，活动空域受限时，三角形航线优于圆形航线。

3.2 巡逻时间受限时四种航线的强效区对比

由于预警机巡逻时间有限制，因此认为巡逻时间相同时，强效区面积越大越好，活动空域越小越好。本节对比巡逻时间相同时，也就是航线周长相同时，强效区面积和活动空域面积。将四种航线两两进行对比。

3.2.1对比跑道形与8字形航线

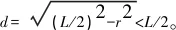
结论1：当跑道形航线与8字形航线的飞行长边相等且转弯半径相等时，跑道形航线活动空域小于8字形航线。

结论2：当跑道形航线与8字形航线的飞行长边相等且转弯半径相等时，跑道形航线强效区面积小于8字形航线。

结论3：当跑道形航线与8字形航线的飞行长边相等且转弯半径相等时，跑道形航线强效区长边对应的最远点近于8字形航线(对比图2(a-b)中OG线段长)，跑道形航线转弯半径对应的最远点远于8字形航线。(由于一般将跑道形和8字形长边朝向目标区域或威胁区域，因此长边对应的强效区最远点越远越好，相对的，转弯半径对应的强效区最远端不太重要。)

综上，巡逻时间受限时，8字形航线优于跑道形航线。

3.2.2对比跑道形与圆形航线

巡逻时间受限时，对比周长相同的跑道形航线和圆形航线的活动空域和强效区面积。

结论1：当跑道形与圆形航线周长相同时，圆形航线活动空域更大。

结论2：当跑道形与圆形航线周长相同时，圆形航线强效区面积更大，但差别不大。仿真证明如图3。当航线周长一定时，圆形航线的半径即为定值，遍历可能的跑道形航线的L和r(遍历r时步长为2 km)，并计算跑道形航线和圆形航线的强效区面积，仿真结果如图3(a)，图3(a)中虚线框内放大后如图3(b)，由图可见圆形航线的强效区面积更大，但优势并不明显。

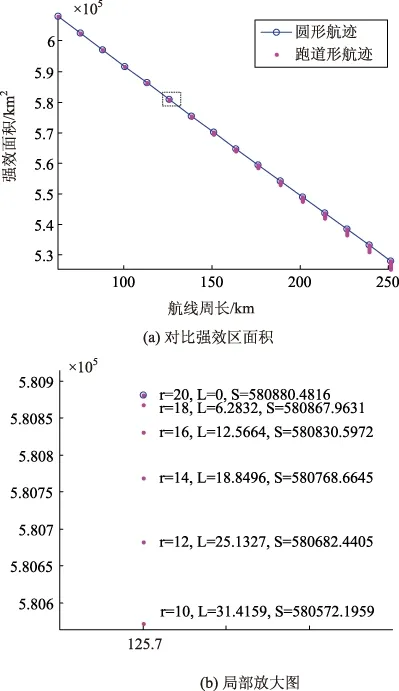
图3 巡逻时间受限时对比跑道形和圆形航线强效区面积对比

3.2.3对比8字形与圆形航线

巡逻时间受限时，对比8字形航线与圆形航线与上一节对比跑道形航线与圆形航线分析方法和结论一致。

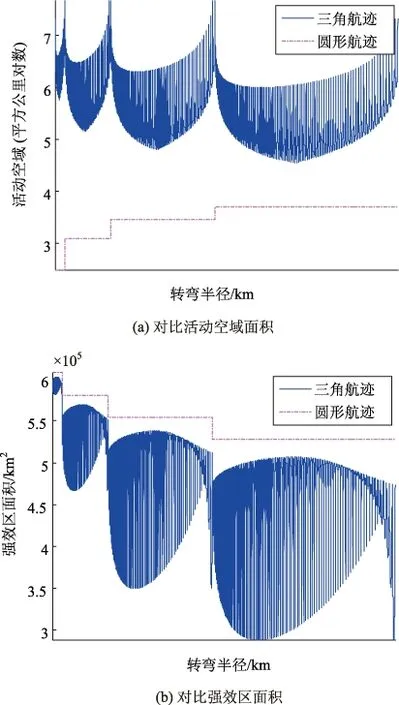
图4 巡逻时间受限时对比三角形和圆形航线

结论1：当8字形与圆形航线周长相同时，圆形航线活动空域更大。

结论2：当8字形与圆形航线周长相同时，圆形航线强效区面积更大，但区别不大。

3.2.4对比三角形与圆形航线

结论1：当三角形航线和圆形航线周长相等时，圆形航线活动空域更小。

结论2：当三角形航线和圆形航线周长相等时，圆形航线强效区面积更大。

综上，巡逻时间受限时，圆形航线优于三角形航线。仿真图如图4，图中的三角形航线与圆形航线的周长相同，当圆形航线的转弯半径分别为10km、20km、30km和40km时，穷举各种可能的三角形边长(边长取整)，并计算三角形航线的活动空域和强效区面积，分别如图4(a)和图4(b)，由图可见，三角形航线的活动空域大于圆形航线，强效区面积小于圆形航线。

3.3 径向速度盲区

预警机雷达通常采用脉冲多普勒(Pause Doppler，PD)体制雷达。由于PD体制雷达本身的局限性，在频域上进行多普勒频移检测时，若机载雷达与目标间的相对径向速度未超出可检测门限，其威力范围与覆盖范围内存在检测盲区，这在雷达情报输出端直接表现为漏情以及目标航迹的不连续，影响机载雷达的整体探测性能，成为战时的薄弱环节。因此本文对比跑道形航线和圆形航线的径向速度盲区。

设预警机载机航向与雷达波束的夹角为α，目标航向与雷达波束的夹角为β，预警机航向与目标航向夹角为γ=α-β，设预警机速度为VR，目标速度为VT，径向速度计算公式为：

Vr=VRcosα-VTcosβ

(25)

当径向速度Vr小于临界值Vmin或大于临界值Vmax，即当|Vr|Vmax时，目标处于盲区。

本文考虑当预警机沿着跑道形或圆形航线巡逻，目标做匀速直线运动的情况，平面示意图如图5。目标航线为蓝色虚线，航线如箭头所示，目标航线的直线方程由OB线段长，和∠θ唯一确定。设当目标在B点时，即目标航线上距离预警机航线中心O点最近的点时，预警机位于跑道形或圆形航线上的Y点。OB线段长b0、θ角度和Y点位置三个变量即可唯一确定目标航迹与预警机航线之间的运动关系。

对于预警机沿跑道形和圆形两种航线巡逻的情况，预警机与目标的空间位置关系可以统一计算。以下均假设预警机沿航线以速率VR逆时针巡航，目标沿任意一条直线做匀速直线运动。以目标飞行经过B点时为零时刻，B点坐标为(b0cosθ,b0sinθ)，目标的匀速直线运动可以等效为目标从零时刻按照两个相反的方向做匀速直线运动，速度分别为(±VTsinθ,∓VTcosθ)，则t时刻目标的位置坐标为(b0cosθ±tVTsinθ,b0sinθ?∓tVTcosθ)。设零时刻预警机在航线上的Y位置，t时刻预警机的位置坐标为(xY(t),yY(t))，该位置预警机的速度矢量为(Vx,Y(t),Vy,Y(t))。设预警机与目标之间的高度差为h。

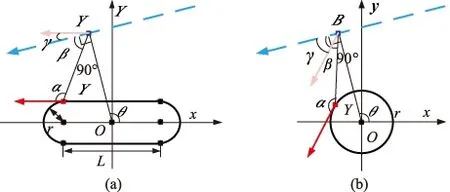
图5 跑道形航线与圆形巡逻航线的径向速度示意图

(b0cosθ±tVTsinθ-xY(t),b0sinθ∓tVTcosθ-yY(t))

(26)

预警机与目标的距离d相对,Y(t)为：

(27)

(±VTsinθ-Vx,Y(t), ∓VTcosθ-Vy,Y(t))

(28)

由以上的相对运动关系，可得t时刻目标相对于预警机的径向速度大小的计算公式为：

(29)

对比跑道形和圆形航线的仿真参数设置如表1，跑道形航线与圆形航线的周长几乎相等，即巡航一周的时间几乎相同、耗油量几乎相同。预警机巡航速度为450 km/h，目标速度为600 km/h，预警机与目标高度为8000 km，高度差h=0 km。在仿真中，设目标沿X轴由左向右飞行，θ=90°；预警机零时刻位置为航线与负Y轴交点；目标在零时刻与预警机航线原点的距离b0的取值为-Rm-r-L/2≤b0≤Rm+r+L/2。

表1 跑道形与圆形航线径向速度盲区对比仿真参数设置

仿真结果如图6所示。图中黑色实线为预警机巡逻航线，为跑道形或圆形；航线上红色圆点为初始时刻预警所在位置Y；紫色点划线为预警机按跑道形或圆形航线巡逻时的强效区；蓝色虚线为目标航线示意，箭头表示航向，与文献[7-9]中仅考虑某一条特定的目标航线不同的是，本文仿真实验中同时仿真了多条θ相同b0不同的做匀速直线运动的目标航线，即与蓝色虚线平行的多条目标航迹。图中黑色区域为预警机与目标相对运动中，目标超出了预警机探测范围的区域，白色区域为目标预警机探测范围内的区域，灰色区域为径向速度盲区。从图6可以看出，预警机运动到跑道形航线长边时，预警机与目标呈同向平行运动，此时径向速度小于Vmin，会出现长时间的径向速度盲区。目标进入盲区后，预警机探测的目标航迹将会中断，中断时间过长，即使目标再次出现，预警机也难以判断是否为同一个目标。

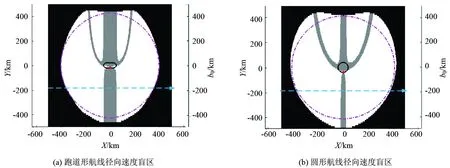
图6 跑道形航线与圆形巡逻航线的径向速度盲区仿真图

4 结 语

本文对预警机四种典型巡逻航线及其预警探测总覆盖区、弱效区和强效区建立数学模型，从活动空域大小、航线周长、强效区面积和径向速度盲区四个方面分析对比了跑道形、8字形、三角形和圆形四种预警机典型巡逻航线，总结如表2。

本文认为圆形航线为最优巡逻航线。采用圆形航线，可以在最小的活动空域内，获得最大的强效区面积；而且圆形航线强效区占总覆盖区的比例最大。圆形航线的另一个显著优点是径向速度盲区影响小。圆形航线可以看作是特殊的跑道形或8字形航线，是跑道形或8字形航线的极限情况，也是跑道形或8字形航线强效区面积最大的情况。美国的E-3预警机和日本的E-767预警机在训练和执行任务中都是采用圆形航线飞行。三角形航线可以看作是特殊的圆形航线，在载机持续转弯能力受限情况下，可以达到近似圆形航线的效果。

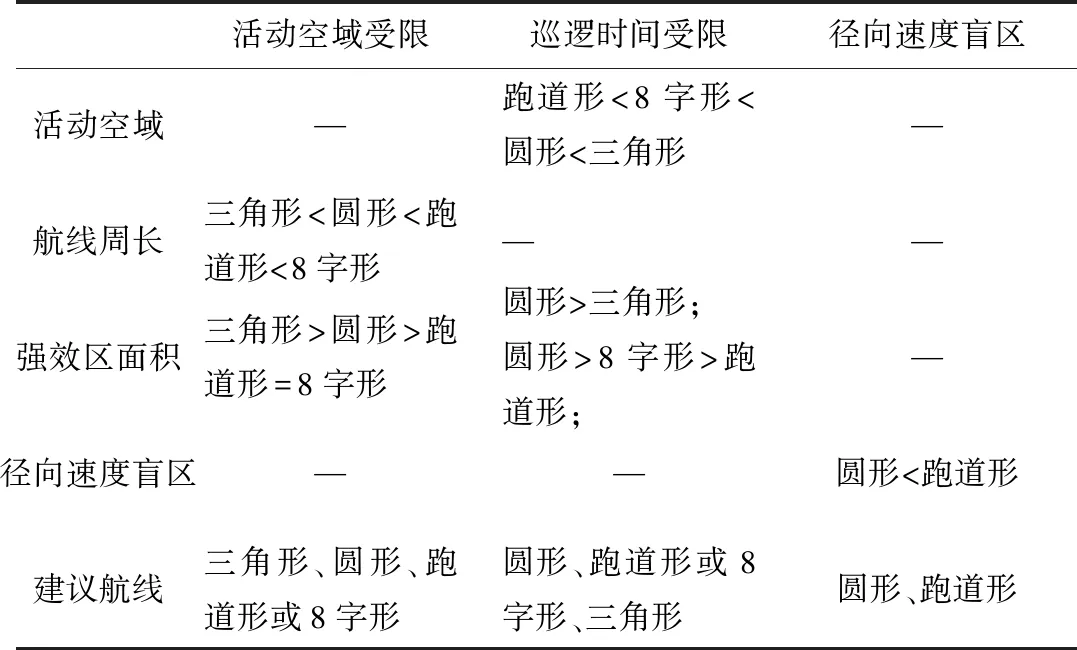
表2 四种典型预警机巡逻航线对比

综上，本文建议预警机在执行预警探测任务中，采用圆形航线巡逻飞行。当不能飞圆形航线时，可采用跑道形或8字形航线。当需要环绕重点区域的巡逻方式，以便全方位监视时，可以采用三角形航线。

本文的不足之处有：对8字形航线和三角形航线的建模还比较简单，没有详细考虑转弯的影响。实际飞行中，载机运动遵循空气动力学特性且具有惯性，并不能按照规整的三角形飞行。分析径向速度盲区时，仅考虑了目标做匀速直线运动的情况，未考虑变速运动和机动转弯等复杂情况。在实际应用中，可以通过建立目标的运动模型，预测径向盲速，并采取措施补偿或规避。此外，本文未考虑各种航线飞行操作的难易程度，如圆形航线对惯导和飞行员的要求较高等。在以后的工作中将完善以上不足。