温室温度精确反馈线性化预测控制

陈俐均，杜尚丰，梁美惠，何耀枫

(中国农业大学 信息与电气工程学院，北京 100083)

0 引言

温室环境调控可为作物提供一个适宜的生长环境，以达到高产、优质、高效的目的[1]。在众多环境调控因子中，温度是影响作物生长的关键因子之一。对于温室温度的调控，由于模型预测控制能够对目标函数进行优化，具有直接处理能量损耗问题，方便考虑被控过程的输入、状态和输出的约束条件等优点[2-3]，深受研究学者们的重视，并取得了一定的研究成果[4-5]。这类算法一般采用二次规划技术寻求最优解，但温度模型具有较强的非线性特性，通常会导致二次规划的非凸问题，且计算量庞大，实际操作过于复杂。

针对此问题，若能够对温室温度系统进行线性化操作，则可以基于线性模型设计控制器，提高在线计算效率，促进预测控制器在实际温室生产中的应用。王向东等[6]利用泰勒级数展式对温室环境模型进行线性化，但这种方法为近似线性化，忽略高阶非线性项，使得线性化模型与原模型存在偏差。以微分几何为基础的精确反馈线性化可以通过适当的微分同胚映射和非线性状态反馈，实现非线性系统状态或输入输出的精确线性化[7]。文献[8-9]将该方法用于温室环境的调控，在线性化模型的基础上采用比例积分微分(Proportional Integral Derivative，PID)控制策略，减小了在线计算复杂度，取得了明显优于传统控制的效果，为该方法在复杂温室环境控制中的应用提供了可能，但控制算法未直接考虑能量损耗问题。

综上所述，本文将输入输出线性化与预测控制相结合，提出了温室温度精确反馈线性化预测控制策略。论文的内容组织如下：①构建温室温度仿射非线性系统； 根据微分几何理论，实现温度模型输入输出精确线性化。②基于线性化系统设计预测控制器，使温度跟踪误差与运行能耗加权的二次型性能指标达到最小。③对所设计的线性化预测控制系统进行仿真验证。

1 温室温度系统精确线性化

1.1 温室温度仿射非线性系统模型

温室内部环境状态的变化由系统中能量和物质的变化情况决定。影响温室能量流和物质流的因素有：控制信号的输入和室内外环境的差异。选取温室空气温度和土壤表层温度为状态变量，外界输入包括太阳辐射和室外温度，控制变量为加热器热量输入。根据能量平衡建立其机理模型[10]，即

(1)

其中，Cg为温室空气热容，Cg=32 000 J/(℃·m2)；Tg为温室温度(℃)，它受到室外太阳短波辐射增热量Qrad(W/m2)、室内空气与覆盖物的热交换Qcov(W/m2)、室内空气与表层土壤的热交换Qsoil(W/m2)、作物蒸腾作用消耗的潜热Qtran(W/m2)及热量输入uh(W/m2)的影响；Cs为表层土壤热容，Cs=120 000J/(℃·m2)；Ts(℃)为表层土壤温度，它与表层土壤向室内空气的对流传热Qsoil(W/m2)和深层土壤向表层土壤的热传导Qd(W/m2)有关。

式(1)中各项的计算公式为

Qrad=ηG

(2)

其中，η为太阳辐射热量转换系数，η=0.7；G为室外太阳辐射强度(W/m2)。

Qcov=kcov(To-Tg)

(3)

其中，kcov为温室覆盖材料的热传递系数，kcov=7.9W/(℃·m2)；To为室外温度(℃)。

Qsoil=ksoil(Ts-Tg)

(4)

其中，ksoil为表层土壤热传递系数，ksoil=5.75W/(℃·m2)。

Qtran=λEtran

(5)

式中，λ为水的汽化潜热，λ=2.45J/kg；Etran为作物叶片蒸腾速率[kg/(s·m2)]，表达式为[11]

(6)

(7)

其中，s为饱和水汽压随温室温度变化曲线的斜率(kPa/℃)；r为湿度计常数，r=0.064 6kPa/℃；rs为作物叶片对水汽的阻抗，rs=100s/m；rb为作物叶片边界层空气动力学阻抗，rb=180s/m；ke为作物冠层消光系数，ke=0.8；LAI为作物冠层叶面积指数；ρa为空气密度，标准条件下ρa≈1.29kg/m3；Ca为空气恒压比热容，Ca=1000J/(kg·℃)；p0为0℃时的空气饱和水汽压，p0=0.610 7 kPa；Λ为理想气体定律中的理想气体常数，Λ=0.461 52 N·m/(℃·g)；Vh为室内绝对湿度(kg/m3)。

Qd=kd(Td-Ts)

(8)

其中，kd为深层土壤向表层土壤的热传导系数，kd=2 W/(℃·m2)；Td为深层土壤温度(℃)。

由式(1)可知：温室模型仅对状态变量为非线性，对控制量是线性的，符合仿射非线性系统的定义。将作物蒸腾速率(6)代入模型(1)中，令状态变量X=[x1，x2]=[Tg，Ts]，室外输入V=[v1，v2]=[G，To]，控制变量u=uh，整理可得单输入单输出仿射非线性系统的标准形式为

(9)

其中，y为系统输出变量；h(X)为光滑输出函数；f(X)和g(X)为光滑的向量场。

(10)

(11)

1.2 温室温度系统输入输出线性化

1.2.1 输入输出线性化理论

所谓输入输出线性化，就是通过构造稳定的状态反馈控制规律，使得输入输出之间具有理想的线性关系[3]。对于单输入单输出仿射非线性系统(9)，得到线性输入输出关系的基本方法就是对输出函数y进行微分，直到得到y与u的直接关系[12]。为了使输入u出现，需要对y进行微分的次数为系统相对阶。

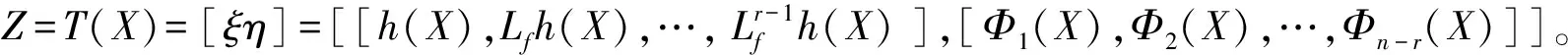
(12)

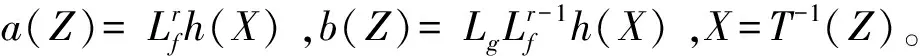
微分同胚T(X)可将原系统分解为外部ξ和内部η两部分，通过状态反馈得

(13)

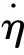
1.2.2 温室温度系统输入输出线性化模型

本节对温室温度仿射非线性系统模型(9)进行输入输出精确线性化。首先计算系统的相对阶，一阶李导数Lgh(X)为

(14)

由式(14)可知：系统(9)的相对阶为1，可采用微分同胚T(X)=[h(X)，Φ1(X)]进行输入输出线性化。

再寻找坐标变换Φ1(X)，需满足条件

(15)

由式(15)可知：Φ1(X)的选取与x1无关，可取Φ1(X)=x2。

据此，利用T(X)可将原系统转换为

(16)

零动态系统f2(0，z2)为线性系统，容易验证z2的系数矩阵为霍尔维茨矩阵，系统渐进稳定。

在新坐标系下，系统(9)的状态反馈控制规律为

(17)

温室温度输入输出精确线性化控制系统如图1所示。

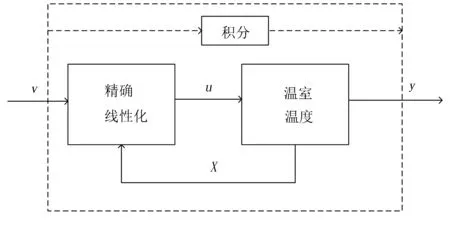
图1 温室温度输入输出精确线性化控制系统框图

2 基于输入输出反馈精确线性化的预测控制器设计

经过上述精确反馈线性化后，系统输入和输出呈线性积分关系。本节在线性化模型的基础上，设计预测控制器，获得加热输入，实现温室温度跟踪和节能功能。基于精确线性化的温室温度预测控制系统结构如图2所示。

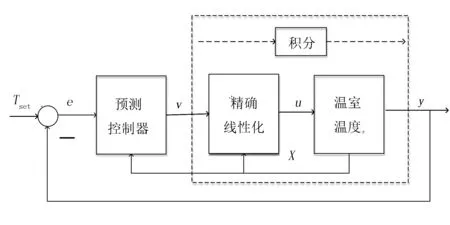
图2 基于精确线性化的温室温度预测控制系统框图

控制的具体过程为：控制器将设定值Tset与系统输出y进行比较，所得偏差e(e=Tset-y)和温室状态X作为预测控制器的输入，经时域滚动优化产生控制量v，传递给精确线性化环节，获得加热控制信号u，调节温室温度。

首先，采用欧拉映射法[13]将系统(16)进行离散化，以输出函数方程为例，可得

y(k+1)=S·v(k)+y(k)

(18)

其中，S为采样周期。

以式(18)作为预测模型，若预测时域为N，则在当前时刻k可得(k+1)～(k+N)时刻的温室温度预测值为

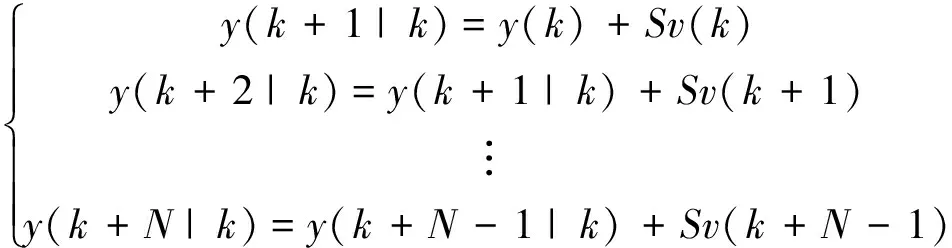
(19)

其中，y(k+i|k)(i=1，2，…，N)为k+i时刻的预测模型输出值。

为使系统在整个控制过程中的动态跟踪误差与加热能量消耗综合最优，构造如下二次型性能指标J，即

u(k+i-1)TRu(k+i-1)]

(20)

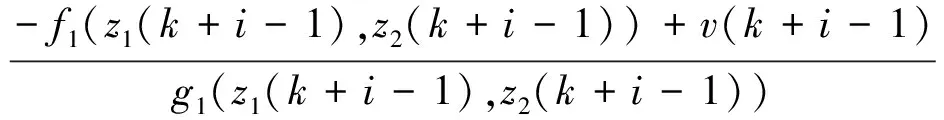
(21)

其中，Q和R分别为跟踪误差和控制量的加权系数，预测时域和控制时域均为N。

受温室加热执行机构结构和容量的限制，控制信号u需满足如下约束条件，即

umin≤u(k)≤umax

(22)

其中，umin和umax分别为加热量的最小值和最大值。

根据式(21)和式(22)，可得新控制输入v在每个控制时域N内的最小值vmin和最大值vmax分别为

vmin(k+i)=uming1(z1(k+i),z2(k+i))+

f1(z1(k+i),z2(k+i))

vmax(k+i)=umaxg1(z1(k+i),z2(k+i))+

f1(z1(k+i),z2(k+i))

i=0,1,...,N-1

(23)

在式(23)的约束下，使性能指标(20)最小化即可得最优控制信号输入。由于动态规划对于解决离散系统二次型性能指标最优控制问题很有效，且可以处理控制变量存在约束的情形，因此选用动态规划作为优化搜索方法。该算法通过优化可找到一个最优控制序列V*(k)=[v*(k)，v*(k+ 1)，…，v*(k+N-1)]；把v*(k)代入式(21)，求得u*(k)；将u*(k)应用于温度控制中，作用时长为1个采样周期，然后时间向前滚动1个采样周期。重复进行此优化搜索，直至进行到终端时刻。

3 仿真试验

为了验证所设计控制策略的有效性，利用Matlab对基于温室温度输入输出精确线性化的预测控制算法进行仿真验证，系统结构如图2所示。仿真系统参数设置为：仿真时间为2天，采样周期S为180 s，预测时域N为3，温室温度和表层土壤温度初值分别为10 ℃和5 ℃，深层土壤温度Td为10 ℃，室内相对湿度为50 %(相对湿度和绝对湿度的转换可参考文献[14])，叶面积指数LAI为1.6，加热输入u的取值范围为0 ～ 150 W/m2，室外光照强度G和室外温度To的设置如图3所示。

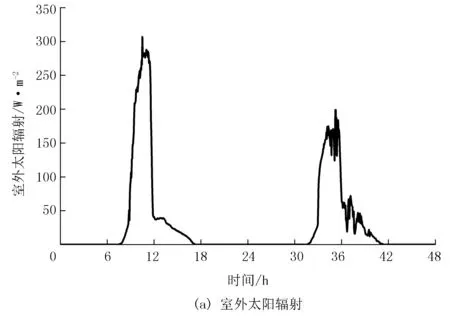
图3 室外太阳辐射和室外温度

采取四段变温方式给出室内温度设定值，具体如下：05：00-09：00，18 ℃；09：00-14：00，26 ℃；14：00-19：00，21 ℃；19：00-05：00，13 ℃。

图4显示了精确线性化预测控制系统在式(20)Q=1、R取不同值时的温室温度跟踪曲线和加热控制量变化曲线。其中，图4(a)、 图4(b)和图4(c)分别为R取1、1.5、2时系统的响应曲线。由图4可看出：R在不同取值下，室内温度基本能够跟踪设定值；随着R的增大，系统越重视消耗能量的大小，温度跟踪能力减弱，加热能耗减小。基于积温思想[15]，作物具有一定的耐受性，短时间内偏离其最适温度，作物生长不会受到太大的影响，故以温度跟踪均方根误差(root mean square error，RMSE)作为控制精度的评价指标。经计算可得：R取1、1.5、2时对应的RMSE分别为1、1.1、1.3℃，加热量的平均值分别为40.4、39.7、38.9 W/m2。在生产应用中，对于权值Q和R的取值，种植者可综合权衡跟踪误差和能量损耗，结合实际情况进行选取。

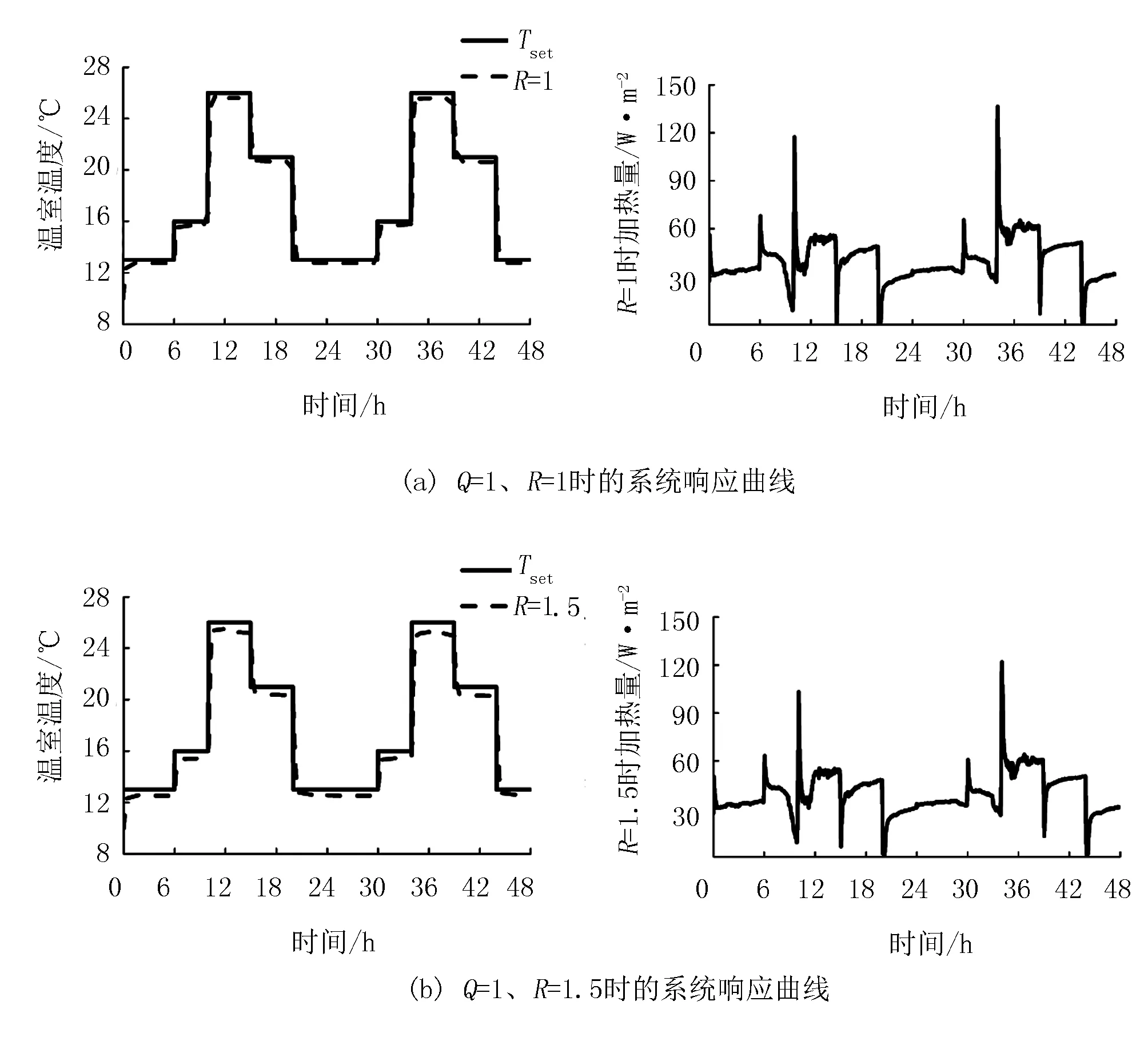
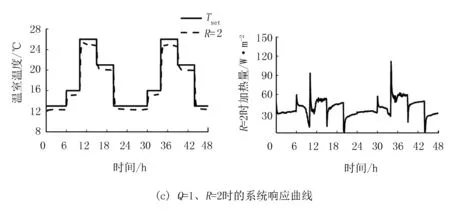
图4 精确线性化预测控制系统在Q=1，R分别取1、1.5、2时的温室温度跟踪曲线和加热控制量变化曲线

为了进一步验证所设计控制系统的调控效果，将其与精确线性化PID控制系统进行对比。PID系统结构与图2类似，只需将预测控制器换为PID控制器即可。预测控制器参数设置为：Q=1，R=1.5；PID控制器参数设置为：比例增益为0.01，积分增益为5×10-4，微分增益为1×10-4。两种控制器其他设置均一致。

图5显示了2种控制系统的温室温度跟踪曲线和加热控制量变化曲线。其中，图5(a)和图5(b)分别为精确线性化预测控制系统和PID控制系统的响应曲线。

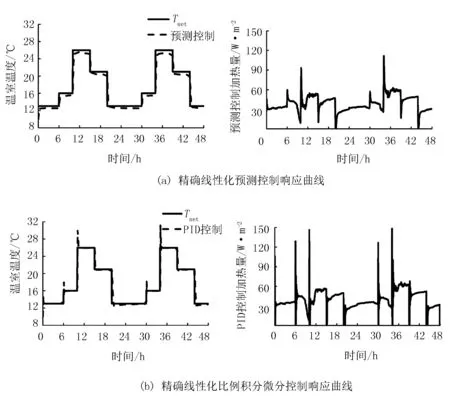
图5 精确线性化预测控制和精确线性化比例积分微分控制的温室温度跟踪曲线和加热控制量变化曲线

由图5可以看出：两种控制器的温度跟踪效果均较好，相比预测控制系统，PID控制系统出现了超调和震荡现象，过大的超调量会导致能量的浪费。此外，在实际温度与设定值出现较大偏差的时刻，两种系统的控制量均及时做出了响应，相比而言，预测控制信号的响应更为平稳。经计算可得：预测控制和PID控制的RMSE均为1.1 ℃，加热量的平均值分别为39.7 W/m2和41.2 W/m2。对比结果表明：精确线性化预测控制系统可以同时兼顾控制精度和加热损耗，更符合实际需求。

4 结论

本文根据能量守恒定律建立了温室温度系统模型，该模型具有很强的非线性特性，但是对于加热控制输入却是线性的，基于此种特点，将其转换为仿射非线性系统。根据微分几何理论，采用精确线性化方法，将输入输出等价为积分系统，再基于等价系统设计预测控制器，该控制器能够综合权衡控制精度与能量损耗，在线计算量小。仿真试验表明，基于精确线性化的温度预测控制器可有效跟踪设定值，与精确线性化PID(Proportional Integral Derivative)控制器相比，在获得相同跟踪均方根误差的情形下，能量损耗更小。下一步的工作是研究温湿度系统的线性化与控制问题，考虑其他设备的调控作用。