多农机重复路径协同作业下的导航路径迭代学习控制

张万枝，刘正铎，郭子蒙，吕钊钦

(山东农业大学 机械与电子工程学院，山东 泰安 271018)

0 引言

农机自动导航技术是实现以提高农业资源利用率、保护农业生态环境为目标的“精准农业”核心技术之一。该技术已成为当前农机装备智能化研究的一个热点方向[1]，主要包括定位技术和路径跟踪技术。定位技术[2]通常采用传感器信息进行车辆位置定位；而路径跟踪技术[3]主要是控制车辆的横向运动，使车辆能够沿着期望路径行驶。因此，路径跟踪的精确程度直接影响了农业车辆的智能行为表现。随着现代控制理论的发展，国内外学者根据一系列现代控制方法对田间作业车辆路径跟踪做了相关研究[4-7]。文献[8]等根据PID控制方法设计了车辆导航横向控制器，能够快速实现车辆的小角度转向，但该方法自适应性和鲁棒性较差；文献[9]根据最优控制算法，设计了具有前馈和反馈的最优控制器，但该控制器对外界干扰较为敏感，横向控制稳定性较差；文献[10]提出一种模糊控制和滑模变结构相结合的车辆横向控制方法，将两种控制思想的优点结合，采用滑模切换函数及其变化率作为模糊控制的输入，具有较强的鲁棒性；文献[11]根据模糊控制算法，设计了车辆横向模糊控制器，模糊规则根据专家经验制定，具有较强的主观性；文献[12]根据传统模糊控制器的不足，利用遗传算法来优化模糊控制器中的隶属度函数和控制规则，取得了较好的路径跟踪效果，但控制器实时性不好。为进一步提高控制器的实时性，文献[13]提出了一种基于改进粒子群优化自适应模糊控制的车辆导航方法，该方法能够迅速消除横向误差，具有超调量小和响应速度快等优点，但其模糊控制规则仍有待进一步优化。文献[14]提出了一种基于模糊自适应纯追踪模型的农机路径跟踪方法，该方法能够实现不同农机速度和初始偏差下的快速跟踪，缺点是预瞄距离易受路径曲率、车辆速度等影响，不能同时保证系统具有较强的跟踪能力和较好的稳定性。

通过分析整个农机作业过程(耕作、播种、施肥、喷药、除草、收获)可以发现，每个作业环节中的农机均按照同一参考路径自动行驶，可看作是“重复路径行驶”，且随着作业环节的深入，对导航精度要求越来越高。针对这种近似重复系统和各作业不同导航精度要求，采用迭代学习控制方法，可以根据过去运行次数的信息，及时修正当前系统的控制输入信号，采用迭代学习逐步提高每次跟踪精度，实现重复系统的期望路径完全跟踪控制。为此，本文提出一种多农机重复路径协同作业下的导航路径迭代学习控制方法。

1 系统描述

在不考虑轮胎与地面侧滑时，农机结构大都可简化为两轮车模型，如图1所示。

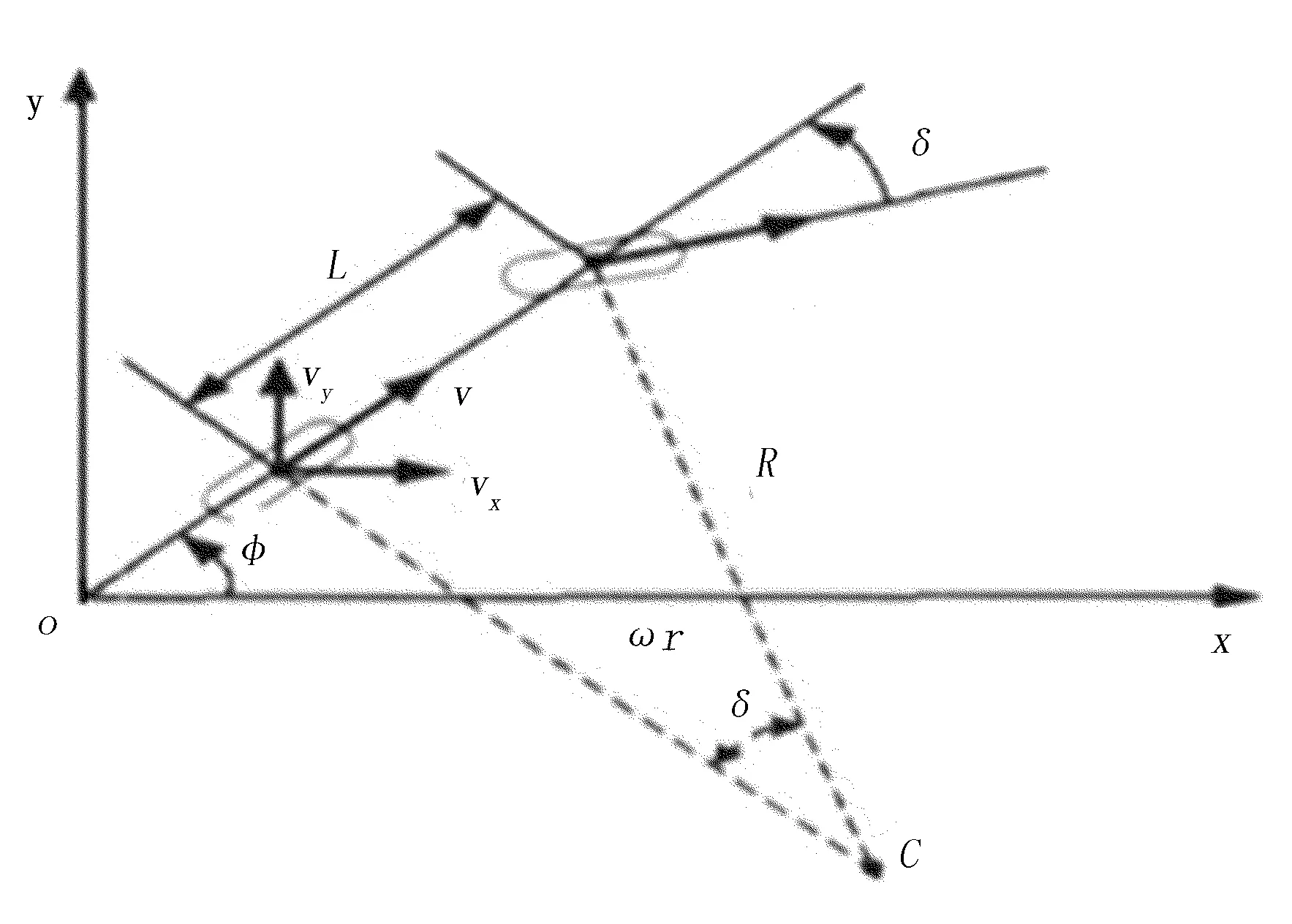
图1 车辆运动学模型

因此，在地面固定坐标系下，车辆的运动学模型可表示为

(1)

其中，(x,y)为车辆后轴中心坐标；φ为车身导航角；δ为前轮转角；v为车辆行驶速度；l为轴距。

根据运动学理论可得

(2)

其中，ω为车辆横摆角速度。

将式(2)带入式(1)，车辆的运动学模型进一步表示为

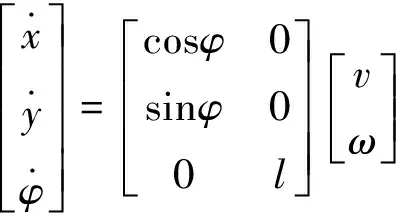
(3)

其中，状态量q(k)=[x,y,φ]T，输入量u(k)=[v,ω]T。可以看出：车辆运动学模型是一个非线性连续系统，需进行离散化处理。离散化的车辆运动学模型可表示为

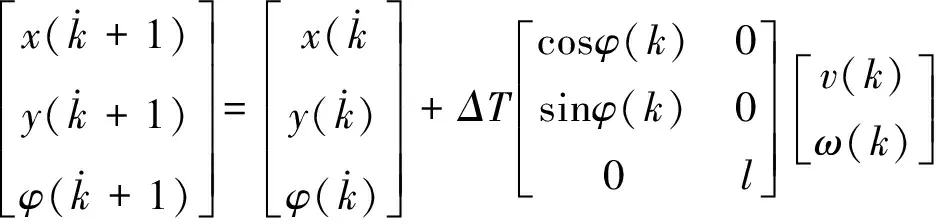
(4)

其中，ΔT为采样时间，1≤k≤n。因此，完整的车辆运动学离散模型可表示为

q(k+1)=q(k)+B(q(k),k)u(k)+β(k)

(5)

y(k)=q(k)+γ(k)

(6)

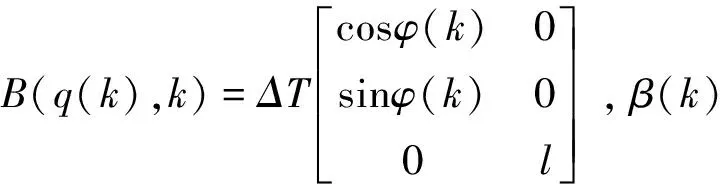
根据图1所示，假定期望路径p(k)=[xd(k),yd(k),φd(k)]T，则路径跟踪的控制实质就是确定输入u(k)=[v(k),ω(k)]T，使得y(k)与p(k)误差最小。

考虑迭代学习初始值相同，由式(5)、式(6)可得

qi(k+1)=qi(k)+B(qi(k),k)ui(k)+βi(k)

(7)

yi(k)=qi(k)+γi(k)

(8)

其中，i为迭代次数；k为离散时间；qi(k)、ui(k)、βi(k)、yi(k)、γi(k)分别表示第i次迭代的状态、输入、输出、状态干扰和输出噪声。由此可以看出，系统方程满足以下性质和假设。

性质1：考虑理想情况，即βi(k)、γi(k)分别为0，则期望路径的跟踪方程为

qd(k+1)=qd(k)+B(qd(k),k)ud(k)

(9)

yd(k)=qd(k)

(10)

性质2：矩阵函数B(qi(k),k)满足Lipschitz条件，即

‖B(q1,k)-B(q2,k)‖≤cB‖q1-q2‖

(11)

性质3：矩阵B(qi(k),k)是有界的，‖B(qi(k),k)‖≤bB，矩阵B(qi(k),k)为(qi(k),k)的满秩矩阵。

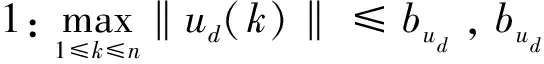
假设3：在每一次迭代中，轨迹都是从qd(0)的邻域开始，即‖qd(0)-qi(0)‖≤bq0，bq0>0，i≥1。

2 迭代学习控制律设计及收敛性分析

采用如下所示的开闭环迭代学习控制律，即

ui+1(k)=ui(k)+L1(k)ei(k+1)+L2(k)ei+1(k)

(12)

对于第i次迭代，跟踪误差信号为ei(k)=yd(k)-yi(k)，L1(k)和L2(k)为学习的增益矩阵，满足‖L1(k)‖≤bL1，‖L2(k)‖≤bL2，k∈N，bL1>0，bL2>0。

通过控制律，使状态变量qi(k)、控制输入ui(k)、系统输出yi(k)分别收敛于期望值qd(k)、ud(k)、yd(k)。可以证明，针对车辆运动学离散模型，满足假设1～3，采用上述控制律，则

‖I-L1(K)B(qi,k)‖≤ρ<1

(13)

对于所有(qi,k)∈Rn×N都成立。如果忽略状态干扰、输出噪声和初始状态误差(即bβ=bγ=bq0=0)，则qi(k)、ui(k)、yi(k)分别收敛于qd(k)、ud(k)、yd(k)。如果考虑干扰、噪声和误差的存在，则‖ui(k)-ud(k)‖、‖qi(k)-qd(k)‖、‖yi(k)-yd(k)‖有界，且收敛于bβ,bγ,bq0的函数。

3 仿真分析

3.1 直线路径跟踪

直线路径方程为

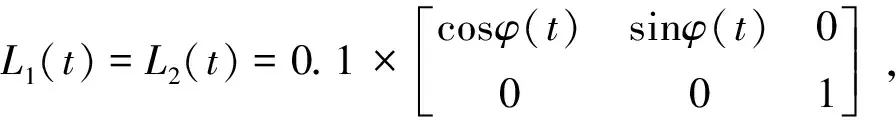
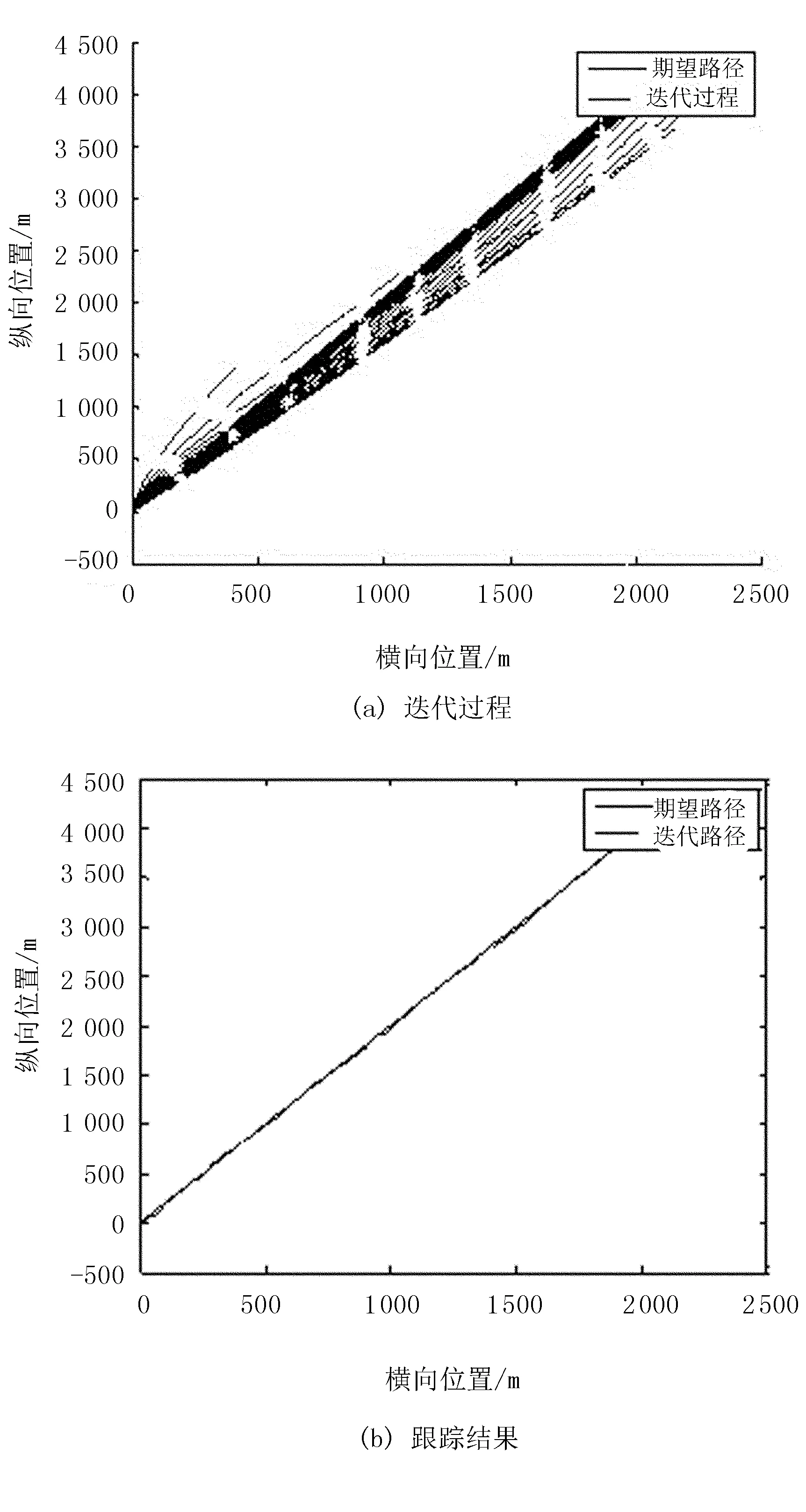
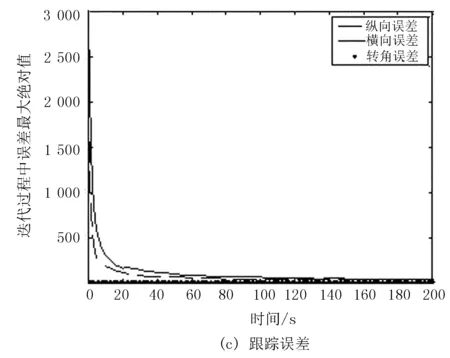
图2 开环迭代学习直线路径跟踪结果

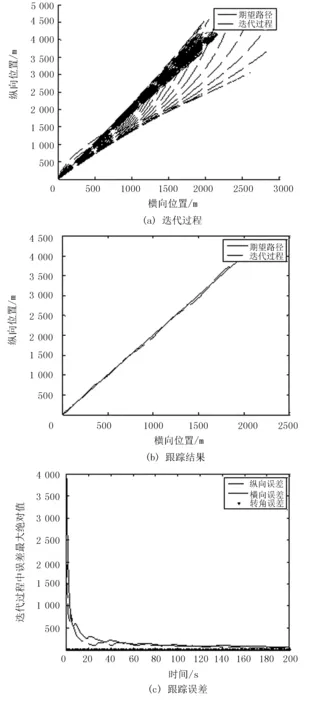
图3 闭环迭代学习直线路径跟踪结果

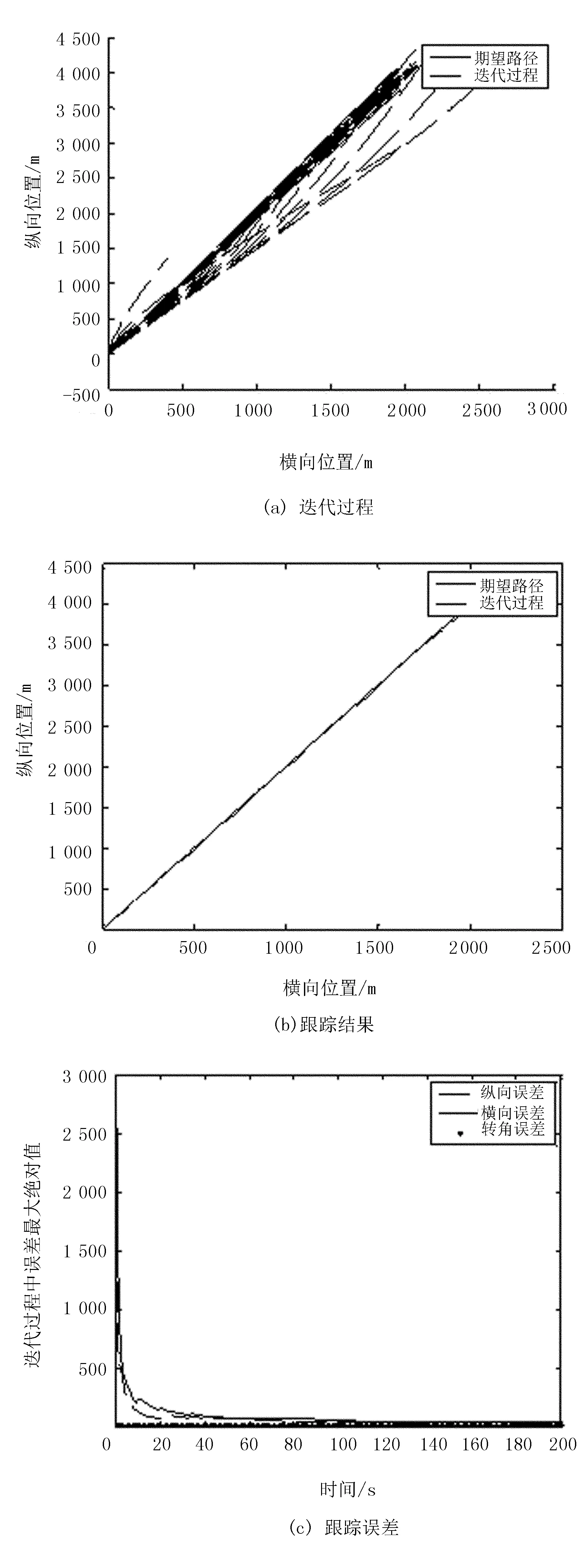
图4 开闭环迭代学习直线路径跟踪结果

由图2～图4可以看出：3种控制律都能使得小车快速跟踪直线路径，跟踪误差均逐渐趋近于0；但与开环、闭环控制律相比，开闭环控制率路径跟踪收敛速度更快。

3.2 圆形路径跟踪

圆形路径方程为

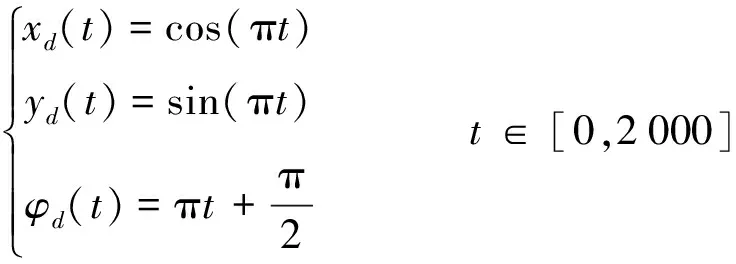
其他参数设置如直线路径跟踪所述。仿真结果如图5～图7所示。由图5～图7可以看出：相同迭代次数下，与开环、闭环控制律相比，开闭环控制律下的圆形路径跟踪效果最好，且跟踪误差逐渐趋近于0。

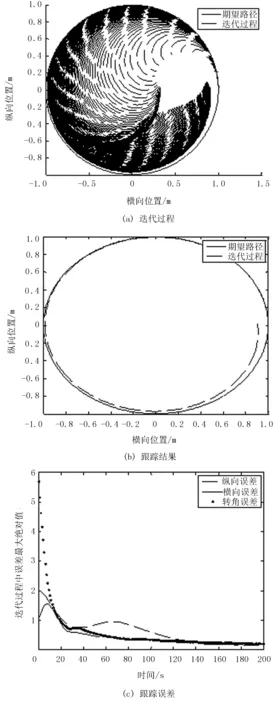
图5 开环迭代学习圆形路径跟踪结果

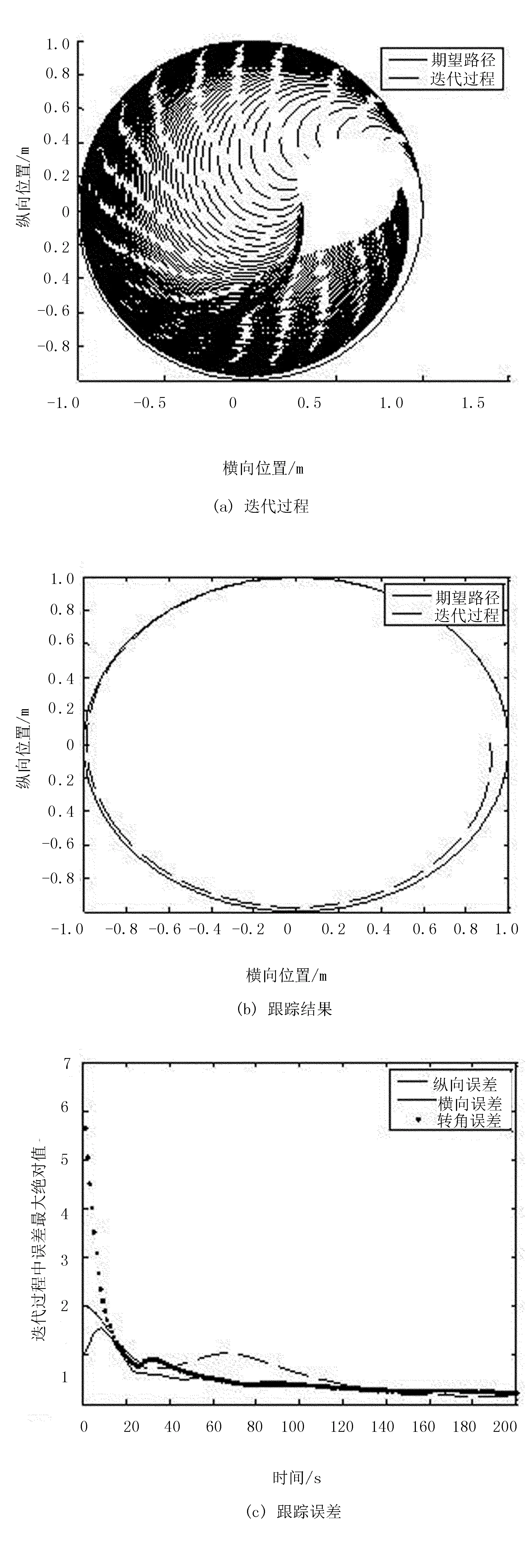
图6 闭环迭代学习圆形路径跟踪结果

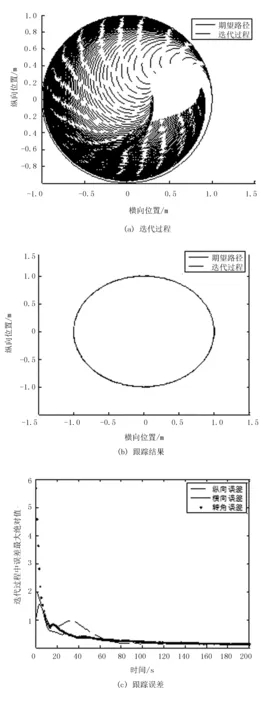
图7 开闭环迭代学习圆形路径跟踪结果

4 结论

基于多农机协同作业时的重复路径行驶特点，提出了一种基于迭代学习控制的农机导航路径跟踪方法。首先，建立了离散的车辆运动学非线性模型；然后，设计了开闭环迭代学习控制律，并进行了收敛性分析；最后进行了直线和圆形路径跟踪仿真实验。结果表明：迭代学习控制能够实现农机导航路径的完全跟踪；相同迭代次数下，与开环、闭环控制仿真结果比较，开闭环迭代学习控制收敛速度更快，路径跟踪误差逐渐趋近于0。该方法可实现农机导航路径的精确跟踪，满足了现代精准农业作业要求。