人工免疫算法优化双支持向量机在拱坝变形预测中的应用

(1.吉林省水利水电勘测设计研究院，长春 130021； 2.河海大学 水利水电学院，南京 210098)

1 研究背景

我国近些年已建或在建一批300 m级高拱坝，如锦屏、小湾、溪洛渡、白鹤滩等，由于缺乏足够的高拱坝安全施工、蓄水、运行经验，拱坝坝体的安全稳定问题一直是工程界较为关心的问题[1-3]。拱坝坝体安全问题分析方法有：仿真计算方法,用来分析不同工况下的变形、应力应变状况[4-6]；采用现场实时监控手段来监测坝体应力、变形是否超出容许范围，是否产生裂缝等[7-8]。其中拱坝变形能够直观反映出坝体是否处于稳定运行状态，由于拱坝坝体变形受到蓄水水压、外界温度、内部水化热、坝体蠕变、混凝土硬化等因子的影响[9]，且各因子之间存在着一定相关性，因而拱坝坝体变形呈现明显的非线性特性，传统的回归统计模型难以表征这一相互耦合作用的非线性关系，难以真实反映出各因子对拱坝坝体变形的影响[10]。

近年来人工智能机器学习方法迅猛发展，在解决数据相互影响、复杂非线性方面的能力有很大提高；作为机器学习方法之一的支持向量机，具有需要数据少、计算速度快，能较好地处理复杂非线性问题的特点，核心思想为把非线性的低维度的样本数据，通过核函数投影到线性的高维度空间中，使得数据之间变为线性关系[11-12]。

标准支持向量机(Support Vector Machine，SVM)最终是求解2组分类数据为一个整体的二次规划问题，计算效率较低，而双支持向量机 (Twin Support Vector Machine,TSVM)通过建立2个非平行的空间超平面，每个超平面均是离一组数据最近而离另外一组数据最远，因此能充分利用输入训练的数据，最终为求解2个单独数据的二次规划问题，极大地提高计算速度[13-14]。同时双支持向量机的泛化学习能力和拟合精度完全依赖于其中的参数，而对于不同的数据，参数的选取也不同，迫切需要一种搜索优化算法来优化双支持向量机的参数，人工免疫算法是一种仿人体免疫系统的遗传算法，能够利用有限的种群抗体得到较为理想的结果。人工免疫算法具有全局性搜索功能，能够有效避免陷入局部最优而使得结果失真[15-17]。

本文选择影响拱坝坝体变形的相关因子，由双支持向量机建立因子与变形之间的输入输出关系，通过人工免疫算法全局搜索优化双支持向量机的参数，拟合拱坝坝体变形量，进而预测未来5 d的拱坝坝体变形。

2 双支持向量机

2.1 双支持向量机模型

双支持向量机(TSVM)与标准支持向量机(SVM)不同之处在于：双支持向量机包含2个非平行超平面，每个超平面都是最接近一组分类数据而尽可能地远离另一组数据。因为只借助2个支持向量，与标准支持向量机相比，能够有效降低分类计算的复杂性：标准支持向量机要解决包含所有2组数据的大二次规划问题，而双支持向量机为分别求解2组数据的小二次规划问题，使得计算速度更快[18-19]。对于给定训练样本集合S=(xi,yi),i=1,…,n，其中：xi∈Rm为m维输入，yi∈R为一维输出。对于输入样本的上下边界，即上下超平面，可以表示为

(1)

式中：w1,w2∈Rn；b1,b2∈R为未知参数；A=[x1,…,xn]T；K(x,xk)为核函数，常用核函数为

K(x,xk)=exp(-‖x-xk‖2/σ2) 。

(2)

式中:σ为核参数；‖*‖表示欧式距离。

超平面方程的求解用优化目标函数表示为：

(3)

(4)

式中：y为输出量；e为单位向量；C1,C2>0，ε1,ε2>0分别为惩罚因子和不敏感参数，作为输入参数；ξ1,ξ2为函数的松弛变量，根据上下边界函数，最终的支持向量机函数为

f(x)=f1(x)+f2(x) 。

(5)

根据Karush-Kuhn-Tucher (KKT)条件，边界函数的对应函数为：

(6)

(7)

最终得：

(8)

2.2 参数选择

参数的选择是否合理直接决定了支持向量机机器学习的泛化能力和对样本数据的拟合精度，而核函数中的参数表征了样本特征子空间分布的复杂程度，数据子空间维度数量直接决定了空间构造的分类面的最大VC维数。双支持向量机参数包括惩罚因子C1,C2，核函数参数σ1,σ2，不敏感参数ε1,ε2，其中不敏感参数与惩罚因子作为一个整体共同影响计算结果，所以在计算中通常固定ε1,ε2，而调整惩罚因子。当样本数据出现个别严重偏离的现象时为避免这些个别点对机器学习造成较大的影响，引入了惩罚因子C1,C2，从而降低这些偏离点的影响，C1,C2的取值小表明对偏离点造成的误差惩罚小，对目标函数的损失也就越小，即容忍这些点造成的影响；C1,C2取值较大则相反。对于非线性问题，核函数的选择对应非线性映射函数的高维特征空间，而不同的核函数参数σ1,σ2代表选取的特征空间不同，直接决定了特征空间的选取是否合理，影响计算精度。

因而需要选取最优的参数，使得计算能够得到最优的支持向量机函数。人工免疫算法具有全局性、搜索速度快的优点，能够较好地优化双支持向量机参数。

3 人工免疫算法

人工免疫算法是一种仿生学算法，即仿生物体免疫系统，用于解决计算机领域问题的新兴算法。免疫系统的一大特点是用有限的资源有效地应对数量庞大且种类多变的病毒入侵。基于这一思想，将免疫概念及其理论应用于遗传算法，在保留原算法优良特性的前提下，力图有选择、有目的地利用待求问题中的一些特征信息或知识来抑制其优化过程中出现的退化现象，这种算法称为免疫算法。

在用人工免疫算法搜索最优参数，求解优化问题时，将目标函数或最优解作为抗原，产生的待选解为抗体，用亲和度来表征抗体与抗原之间的匹配程度，当亲和度越大，说明两者匹配效果越好，该抗体值越接近最优解，在下一代交叉中赋予较高的抗体浓度，即繁殖下一代时给与较高概率。

图1 人工免疫算法流程

图1为人工免疫算法流程，具体的人工免疫算法步骤为：

(1)抗原识别，将计算的目标函数作为抗原。

(2)确定抗体编码，生成N组抗体值，进行二值化编码。

(9)

(4)更新记忆单元，将亲和度最高的抗体进行标记，在下一代抗体中仍保留该抗体。

(5)判断是否符合条件，判断计算的亲和度是否满足要求，当满足要求时即停止计算，若不满足要求转到步骤(6)。

(6)促进和抑制抗体的产生。计算每个抗体的期望值，抑制期望值低于阈值的抗体；可以知道与抗原间具有的亲和力越高，该抗体的克隆繁殖数目越高，其变异率也越低。抗体期望值可以用抗体浓度来表示，抗体浓度为

(10)

其中,

式中：N为抗体组数；cv,w表示第w组的抗体浓度；a为判别系数;yv,w为第w组抗体值；Tac1为预先给定的阈值。

(7)克隆变异抑制，对于上一代中的记忆单元及亲和度高的抗体在克隆中赋予较高的概率，而对于抑制的抗体赋予较低的克隆概率、较高的变异概率。

(8)将新的抗体代入计算，转到步骤(3)。

4 人工免疫算法优化双支持向量机

在上文双支持向量机参数选择中提到，参数的选择对双支持向量机的拟合效果影响很大，需要通过人工免疫算法对双支持向量机参数进行优化，需要优化的参数有C1,C2,σ1,σ2，流程如图2，具体步骤为：

图2 人工免疫算法优化双支持向量机参数流程

(1)确定目标值(抗原)。对于应用双支持向量机拟合监测变形数据问题，监测得到的变形值为抗原。

(2)选择参数。支持向量机中待优化的参数有C1,C2,σ1,σ2，根据数据经验确定各参数大致范围，建立4组参数体系，每个参数建立N个抗体，即建立4×N个抗体群，对每个抗体值进行二值化编码。

(3)计算双支持向量机。将4组参数分别代入支持向量机中，进行拟合计算，得到拟合值。这里需要说明，待优化的参数是直接抗体，但并非与监测变形值(抗原)直接匹配，而是通过将参数代入TSVM中计算得到变形拟合值与抗原直接匹配。

(4)构造亲和度函数。抗原即监测变形值，当抗体群代入支持向量机后得到拟合值，则原始值与拟合值之差的绝对值的倒数为亲和度函数。

(5) 更新记忆单元。将与抗原亲和度特别高的抗体进行标记，并用新加入的抗体取代与其亲和性最高的原有抗体，即保留本代抗体中的最优抗体。

(6) 判断是否符合条件。判断每一个可行参数对应拟合值的亲和度是否符合要求，当亲和度不符合要求时(平均误差在1 mm内)，需要进一步计算抗体浓度，即可用于下一代交叉繁殖的抗体的概率。当亲和度完全符合要求则停止计算，提取计算结果。

(7)促进和抑制抗体的产生。选择与抗原接近的抗体，剔除与抗原相差较大的抗体。

(8)克隆变异抑制。通过交叉繁殖下一代抗体。

(9)将新的抗体代入计算，转到步骤(3)。

5 算 例

某水电站位于我国西南地区雅砻江干流，系雅砻江中下游的龙头水电站，工程以发电为主，兼有防洪功能，主要建筑由混凝土双曲拱坝、坝后部位水垫塘和二道坝、右岸地下厂房和右岸泄洪洞组成。坝顶高程1 885 m，最大坝高305 m,坝顶宽16 m，坝底宽63 m，坝身有4个表孔、5个深孔、2个放空底孔。

大坝坝址区主要断层发育包括左岸的f2、f5、f8、f38-6、f42-9断层和右岸的f13、f14、f18断层等。

坝体及坝基布置了垂线以监测坝体坝基径向和切向位移，典型坝段11#，13#具体布置如图3所示。

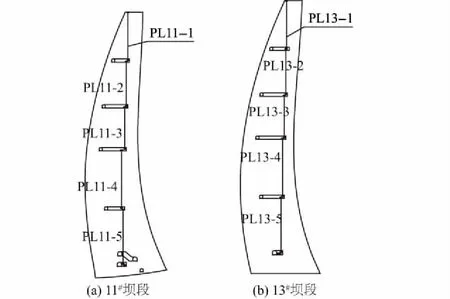
图3 11#坝段和13#坝段垂线布置

针对2015年6—10月的蓄水情况，对坝体位移量进行拟合，监测点为垂线PL11-1和PL13-1，样本数据其中80%用于样本学习，20%用于验证。

为更好地说明双支持向量机的参数对拟合结果的影响，选取不同C值对PL13-1监测点数据进行拟合，拟合结果与实测对比如图4所示。

图4 惩罚因子对拟合效果的影响

由图4可知，当惩罚因子C取值较小(C=0.1)时，拟合曲线为一条水平线，即输出值不随输入值变化；当C逐步增大时，输出值逐步向实测值靠近，进一步说明惩罚因子取值对双支持向量机的拟合效果影响较大。

经人工免疫算法搜索寻优得到双支持向量机最优化参数如表1所示。

表1 人工免疫算法搜索最优双支持向量机参数

将最优参数代入双支持向量机进行拟合，拟合结果如图5所示，可以看出拟合效果较好，同时对PL11-1，PL13-1两个测点进行5 d位移增量预测(相对初始监测值),结果见图6。5 d中PL11-1预测最大误差为1 mm;PL13-1预测最大误差为0.87 mm。

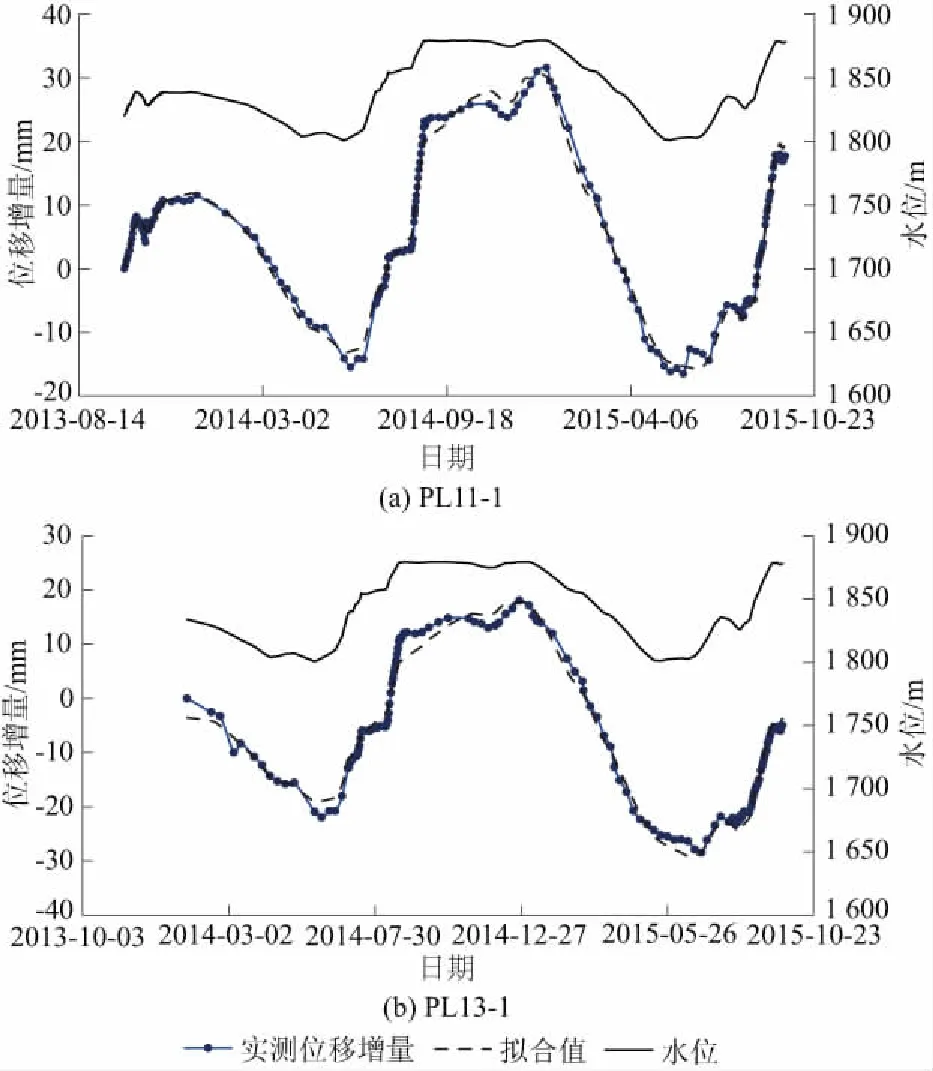
图5 位移增量过程线

从原理出发可知，TSVM相比于SVM的优势在于提高计算速度，而非计算精度，故而TSVM和SVM的计算结果值基本一致。在计算速度上TSVM有极大的提高，进行一次计算，SVM耗时10 s，而TSVM耗时1.6 s，在多次参数优化计算中可以发现TSVM能够明显提高计算效率。

6 结 论

本文考虑双支持向量机能够充分利用样本数据只需求解2组小的规划问题，提高计算速度，将其应用到拱坝变形监测数据分析中，由于双支持向量机参数多且输出结果对参数取值较为敏感，提出应用人工免疫算法全局搜索寻优双支持向量机参数，得到较好的输出结果，具体结论如下：

(1)双支持向量机通过建立2个非平行的超平面来拟合样本数据，使得样本数据能够充分利用，相较于标准支持向量机，只需要求解2组小的二次规划问题，而不像标准支持向量机一样求解一组大的整体二次规划问题，极大地提高了计算速度。

(2)双支持向量机参数较多，且参数的取值对结果输出影响较大，而人工免疫算法具有全局搜索、自动筛选种群提高搜索速度的特点，同时人工免疫算法在遗传算法的基础上保留了一定数量的较优解，提高了算法的计算效率，因此应用人工免疫算法搜索寻优双支持向量机参数，可以得到较好的拟合结果。

(3)应用人工免疫算法优化的双支持向量机对拱坝变形数据进行拟合分析及预测，参数对预测结果的敏感性分析表明，参数变化对拟合效果影响较大；搜索优化后的参数计算结果表明拟合、预测效果较好，最大预测误差仅为1 mm左右。