基于应力与速度时程分析的边坡开挖爆破裂纹扩展研究

梁 瑞1，王树江1，周文海1，黄小彬2，熊征宇，王建勇

(1.兰州理工大学 石油化工学院，兰州 730050； 2.福州大学 爆炸技术研究所，福州 350116；3.紫金矿业建设有限公司，福建 龙岩 364200)

1 研究背景

爆破产生的裂纹裂隙对地面及地下结构具有很大影响,因此，对爆破裂纹裂隙扩展规律的研究在岩体爆破工程中具有重要意义。国内外学者采用理论分析、试验及数值模拟等多种手段对岩体爆破过程中裂纹扩展进行了诸多研究。王明洋等[1]运用应力波的传播理论，分析了在节理带中应力波的衰减规律得到裂隙带越破碎,耗能越大。Munjiza等[2]通过建立爆破近、远区域的损伤断裂准则和裂纹尖端的损伤模型，分析得到裂纹扩展过程是裂纹尖端附近岩石的逐渐损伤区域移动过程。杨小林等[3]利用模型试验研究了爆破振动波在岩体裂纹中的传播规律，得到随裂隙深度的增大，爆破振动波振速减小。潘长春等[4]通过试验研究爆破时裂纹扩展过程，该方法考虑了岩体本身存在的节理面，通过节理断裂模拟裂隙拓展。杨仁树等[5]以有机玻璃(Polymethyl Methacrylate，PMMA)为试验材料，结合模型试验与模拟分析，研究了爆炸应力波与爆生气体对介质的作用效应，得到爆炸应力波是产生粉碎区微裂纹的主因，爆生气体作为主要动力促使裂隙区裂纹形成。彭建宇等[6]利用ANSYS LS-DYNA数值模拟研究单向静应力对爆破裂纹的影响规律及机制，分析了在不同单向静载下裂纹区形状演化规律并得出静应力不影响岩体内应力波衰减规律，但能改变岩体不同位置的应变分布。马波涛等[7]运用LS-DYNA分别对深孔三孔齐发起爆和深孔三孔逐孔起爆的爆生裂纹扩展机理进行了数值模拟，得到采用逐孔起爆法使岩石的自由面发生改变，炮孔破坏更为严重，对爆破效果产生很大的影响。钟波波等[8]通过对模型预置裂纹在双向动载荷下的扩展方式的研究，得到双向动载荷下，随着载荷比率的减小，裂纹沿竖直方向扩展。根据现有研究成果，爆炸应力波和爆生气体对岩石爆破作用所形成裂纹的定量关系依然不明确。本文通过LS-DYNA模拟边坡单孔爆破中岩石裂纹扩展过程，结合应力波衰减规律与裂纹尖端单元的初末平均应力、速度变化率之间关系，进一步探讨应力波衰减与裂纹尖端扩展状态的关系。

2 模型结构及材料参数的选取

2.1 模型构建

为进行边坡爆破裂纹裂隙过程的分析，选用某一露天高陡边坡深孔爆破为背景，建立单孔起爆三维实体模型。边坡台阶高度H为12 m；为了防止坡度过大(>70°)导致上部硬岩大块和坡度过小(<60°)导致下部硬岩留根，本台阶坡面角α选取70°。炮孔布置方式平行于边坡面，底盘抵抗线Wd为3.36 m，炮孔孔径d为150 mm，孔深L为15.27 m，包含超深h为2.5 m，上部堵塞长度Lp为4 m。参照Ma[9]等研究经验确定模型整体规格，台阶下部平盘与台阶上部平盘均取10 m长度，以便于观察模拟爆破过程中裂纹的充分扩展。坡面台阶高度取12 m，下层台阶高度8 m。

(1)在考虑节省运算时间和空间的条件下，并要求动态显示爆破过程中岩体裂纹裂隙萌生、扩展、终止等过程，将模型厚度定义为一个单元厚度。由于数值模拟范围有限，与实际爆破工程有一定误差，为了减小误差对模拟的影响，一般在模拟过程中添加人工边界条件。结合边坡台阶爆破的特点，对模型设置无反射边界条件，约束台阶底面和左右边界面。对于整个爆破过程的所有材料均需施加重力约束，重力加速度取9.8 m/s2。本模拟选用孔底反向起爆方式。具体模型如图1所示。

图1 边坡三维模型

2.2 材料类型及参数

2.2.1 岩石材料

假定岩石为满足各向同性的弹塑性材料，选用*MAT-PLASTIC-KINEMATIC作为其材料类型。表1列出了岩石材料类型的有关参数。

表1 岩石材料类型参数

注：ρr为岩石密度；Er为岩石弹性模量；υ为泊松比；σ0为屈服应力；β为硬化系数；m为材料系数;KIC为断裂韧性。

2.2.2 炸药材料

炸药选取2#岩石乳化炸药，其材料类型为：*MAT-HIGH-EXPLOSIVE-BURN。炸药状态方程选取不考虑炸药产物成分的JWL方程。

炸药的JWL方程[10]为

式中：PCJ为爆轰产物压力;E0为初始比内能；V为爆轰产物的相对比容;A,B,R1,R2均为材料参数;R1,R2为无量纲参数;ω为格林爱森常数;V0为相对体积。

参考文献[11]，列出了炸药状态方程的有关参数，如表2所示。

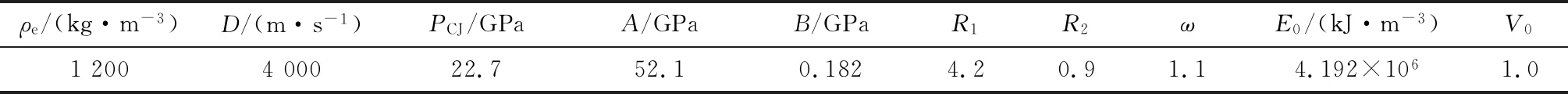
表2 炸药状态方程参数

注：ρe为炸药密度；D为爆速。

2.2.3 堵塞材料

选用炮泥进行堵塞，其材料类型为*MAT-SOIL-AND-FOAM。参考文献[12]，给出堵塞材料类型的有关参数:堵塞材料密度ρb为1 800 kg/m3,堵塞材料弹性模量Eb为0.16 MPa，泊松比为0.3。

3 数值模拟分析

3.1 爆破主要阶段裂纹模拟分析

基于边坡单孔爆破模型，分析炸药起爆后岩体内部裂纹裂隙的形成、扩展过程。爆破过程宏观表现特点为时间极短且能量释放极高，对岩体造成短时间内的高能冲击；微观表现为多个连续耦合作用的岩石破裂过程。爆破在各阶段内造成岩石破损的主要因素不同，不同学者对爆破过程所运用的理论公式与分析方法不同，因此未形成一致定论。一般爆破破坏过程大致分为爆轰波、爆生气体作用2个阶段,本文将对爆破过程主要阶段的不同裂纹处单元应力与速度变化规律进行分析。边坡爆破裂纹模拟结果如图2。

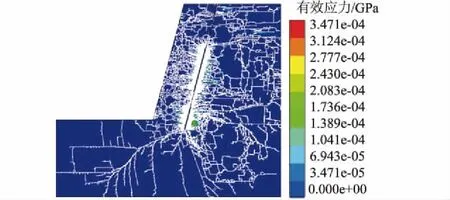
图2 爆破裂纹分布

在ANSYS/LS-DYNA爆破数值计算中，用Von Mises有效应力来表征岩石的应力特性，其分析结果得到了业界的认同和广泛应用。Von Mises屈服准则可以简单地表述为当某质点的应力状态对应的应变能等于极限数值K时质点开始进入屈服状态。公式表示为[12]：

J=Gsijeij=K2。

(2)

式中：J为屈服不变量；sij为偏应力，i和j取值为1，2，3；eij为应变偏量，eij=sij/(2G)；G为材料剪切模量;K为材料屈服特征参数。

Mises屈服条件有效应力σe形式可表示为

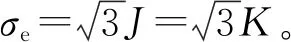
3.1.1 爆轰波动态作用

在第1阶段，爆炸冲击波首先作用于半径为R的炮孔孔壁，冲击波应力强度远大于岩石应力屈服强度，该范围岩石结构在强烈压缩作用下粉碎破坏，形成(2～3)R范围压碎区。该作用圈半径很小，能量消耗很大，冲击波快速衰减为应力波。径向应力波派生的切向拉应力向自由面方向作用，形成初始径向裂纹,一般径向裂纹范围为(2～6)R并形成较密集的微小裂纹。如图3(a)，在Mises应力云图中，药柱端部等效应力波以球状波向外扩展，表征端部药包爆轰波传播状态。选取药柱左侧径向裂纹处单元H12902，该单元应力与速度时程曲线如图3(b)所示，在400 μs时单元有效应力达到峰值，单元速度达到极值，在有效应力逐渐衰减为0后发现单元速度仍持续增大，表明径向微裂纹处不仅受爆轰波动态作用，还受爆生气体作用。

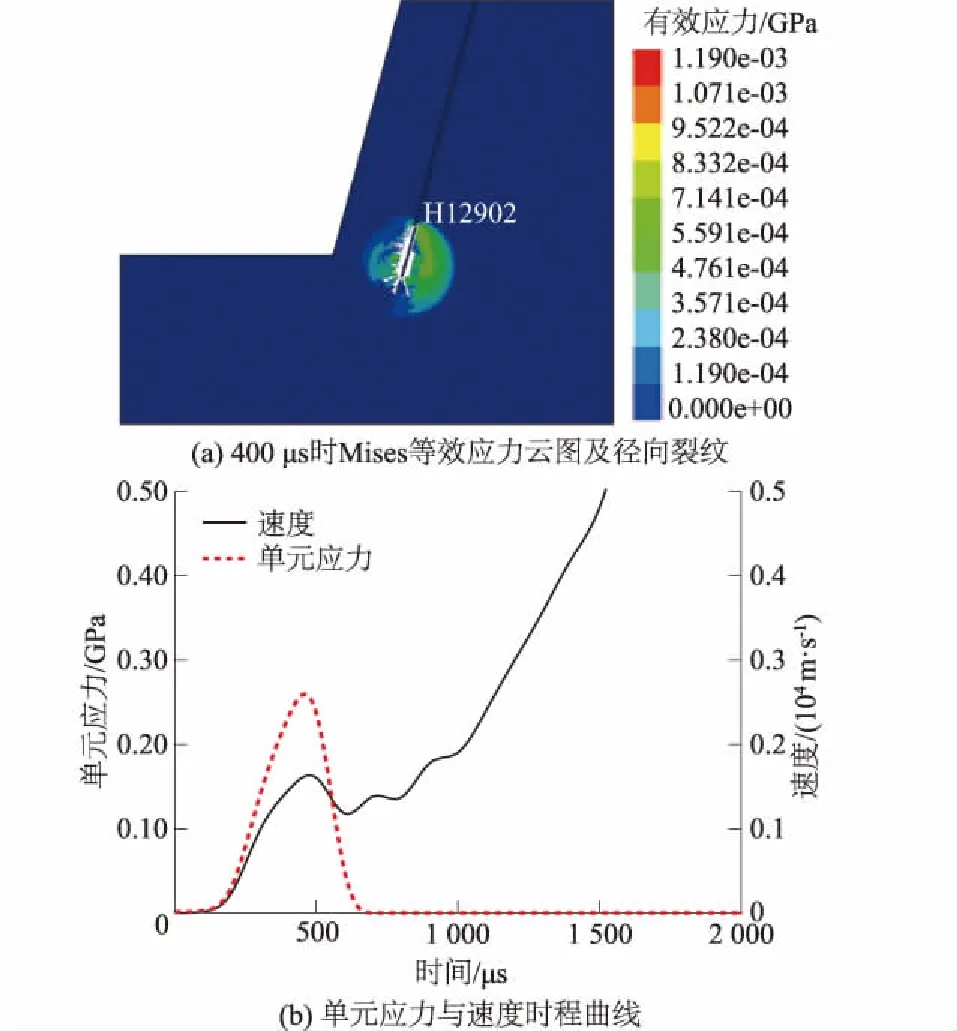
图3 爆轰波动态作用

3.1.2 反射拉伸波作用

爆炸应力波传播至自由面后在岩石介质中产生反射拉伸波。如图4(a)在900 μs时，应力波到达台阶坡脚处的自由面并产生反射拉伸波，对自由面处反射拉伸波通过的单元进行时程分析，选取层裂处单元H12697作有效应力与速度时程曲线。如图4(b)在700 μs时单元达到应力极值，900 μs时，层裂纹尖端有效应力为0.096 3 GPa。在一次应力波作用下，岩石初始的抗拉强度下降至损伤抗拉强度STd,STd=(1-D)ST,ST为岩石抗拉强度[13-14]。因此，自由面处岩石层裂裂纹由一次应力波在自由面反射形成反射拉伸波与二次应力波叠加的拉应力造成，并且层裂纹沿自由面平行方向逐层扩展。同时，爆破过程中采用底部起爆产生的应力波在自由面上首先作用于坡脚处。此处应力状态复杂且介质阻抗性较强，若爆破不充分容易导致留根现象影响爆破效果。应考虑利用自由面附近的层裂纹分布与扩展可提高边坡爆破效果。

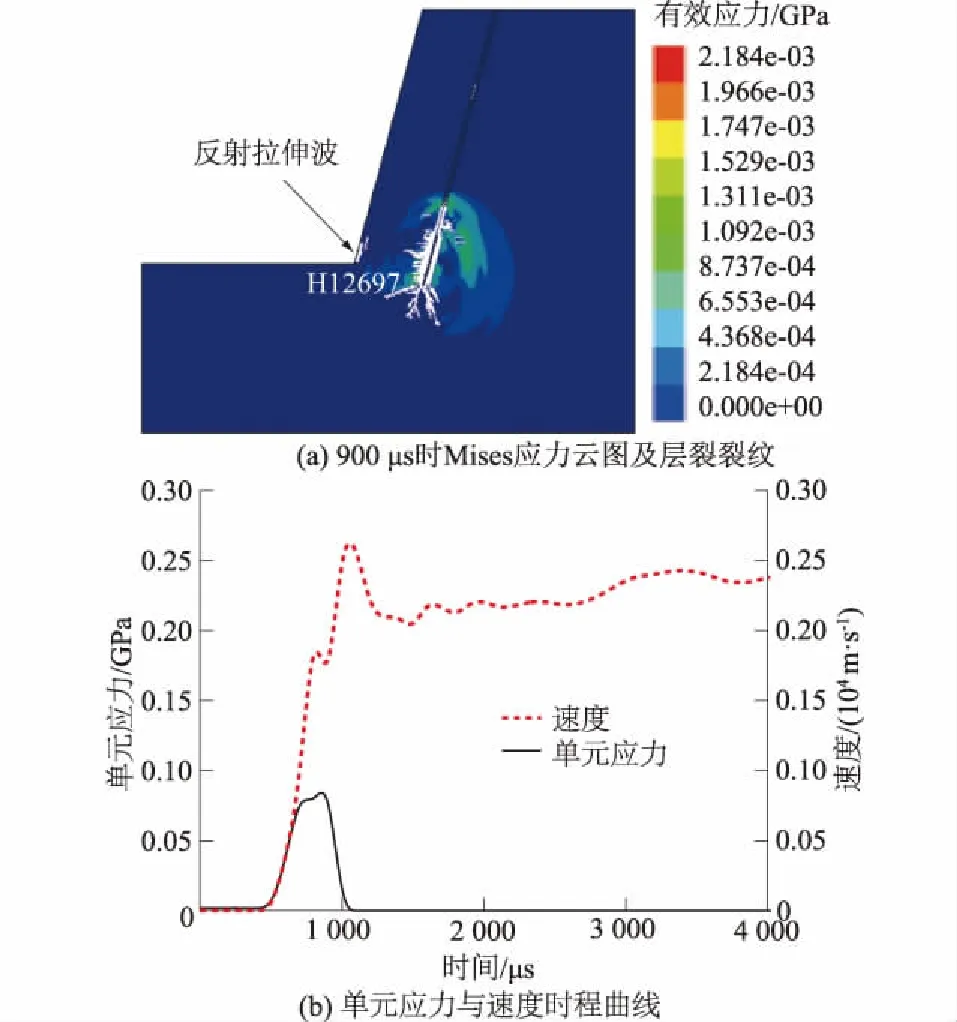
图4 反射拉伸波作用

3.1.3 爆生气体准静态作用

在第2阶段，爆生气体迅速进入径向裂纹并直接作用于裂纹缝隙中，由气楔作用引起岩石质点产生径向位移导致岩石内产生剪应力。当剪应力大于岩石抗剪强度时，岩石失稳破裂形成初始裂纹。一般初始裂纹范围为(3～20)R，破坏形式多以拉伸破坏为主。在爆生气体作用下，采用断裂力学中的应力强度因子KI作为裂纹扩展准则。裂纹扩展条件为：KI=KIC。由线弹性断裂力学，裂纹尖端的应力强度因子计算公式为[15]：

(4)

(5)

(6)

式中：p(r)为压力分布函数；a为裂纹尖端长度；r为裂纹扩展半径；KIC为岩石断裂韧性；N为裂纹条数；f为<1的系数；f∞为<1的远场系数；r0为炮孔半径；σ∞为远场应力。

爆生气体准静态作用效应如图5所示。

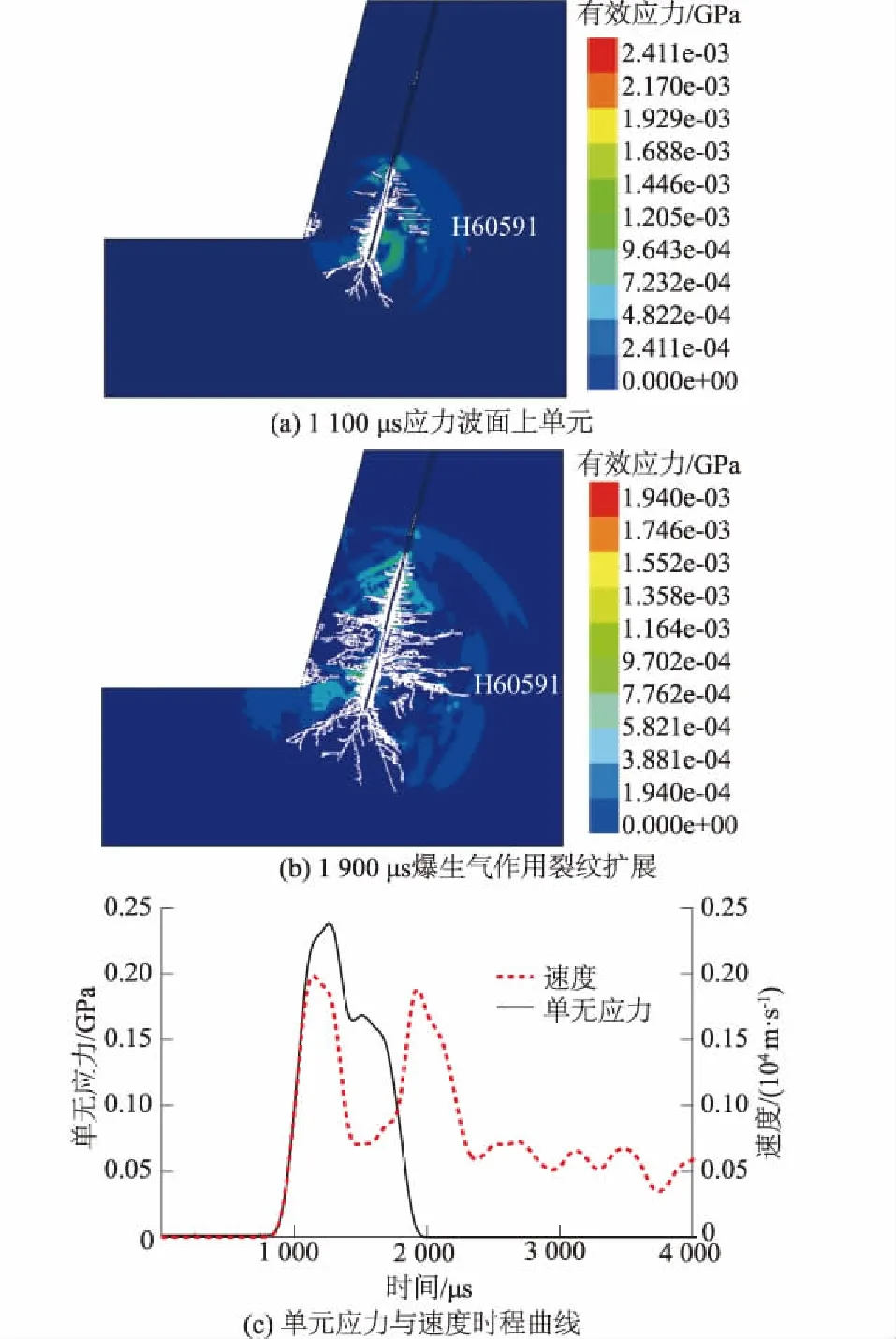
图5 爆生气体准静态作用效应

如图5(a) ，在1 100 μs时应力波传播到单元H60591处，图5(b)中单元首先在应力波作用下达到速度峰值；如图5(c)随着应力波传播并衰减为0，在1 900 μs时该单元速度又迅速上升到极值；结合图5(b)，在1 900 μs时裂纹尖端恰好扩展到该单元处，单元速度产生突增，表明裂纹受到爆生气体作用影响。爆生气体以准静态作用于炮孔壁，在之前由应力波冲击产生的径向裂隙中聚集，导致单元处裂纹尖端应力强度因子KI≥KIC，从而产生径向裂纹扩展。图5(c)中由时间轴长度对比得到爆生气体作用时间比应力波作用长，在介质中形成准静态应力场，有利于裂纹扩展。

假设模型岩体为各向同性的弹性介质并具有线弹性性质,本构方程应符合广义虎克(Hooke)定律：

(7)

(8)

式中：P为静水压力;ε为体积应变;Sij为应力偏量;G为剪切模量;K为体积弹性模量;eij为应变偏量;δij为Kroneker符号;εij为应变。

由于不同药包形式应力波衰减系数相差约35%,球状药包衰减系数远大于柱状药包。本文中模型的条形药包可分为柱部与端部两部分，端部产生的应力波近似球面波,柱部产生的应力波近似柱面波。同时，两药包形式均满足广义虎克定律的本构方程并具有相同形式，即

(9)

式中:σz为竖向应力;σr为径向应力；σθ为切向应力；n1,n2,nz为系数，对于球面波n1=2，n2=0；对于柱面波n1=1，n2=1;εr为径向应变;εθ为切向应变。

根据哈努卡耶夫对于岩体中球面应力波衰减规律，给出球药包径向应力衰减方程[16]，即

(10)

由本构方程条件，球状药包和柱状药包径向应力衰减方程，可写为同一方程，即

(11)

爆破药包为柱状药包时n=2，爆破药包为球状药包时n=1。在岩体爆破中，柱状药包爆破应力衰减系数是球状药包爆破应力衰减系数的1/2，即球状药包爆破应力衰减率是柱状药包爆破应力衰减率的2倍。

3.2 裂纹扩展的应力与速度模拟分析

基于爆破应力波衰减系数分析应力与速度对裂纹扩展的影响，分别选取药柱左侧、右侧、下侧3条较显著的裂纹，并分别选取每条裂纹扩展路径上的单元进行应力与速度时程分析。所选取的单元均为裂纹在该时刻的裂纹尖端单元。

在下侧裂纹(裂纹1)依次选取单元为H45914、H45902，位置如图6(a)；分别作出2个单元的应力与速度时程曲线，如图6(b)；单元H45914在1 200 μs时为裂纹1尖端，单元应力为0.343 GPa，速度为0.778×104m/s；1 300 μs时裂纹尖端扩展到单元H45902处，单元应力为0.627 GPa，速度为0.751×104m/s。经计算，随时间增加裂纹1的两单元间应力增大82.80%，速度增大3.5%。

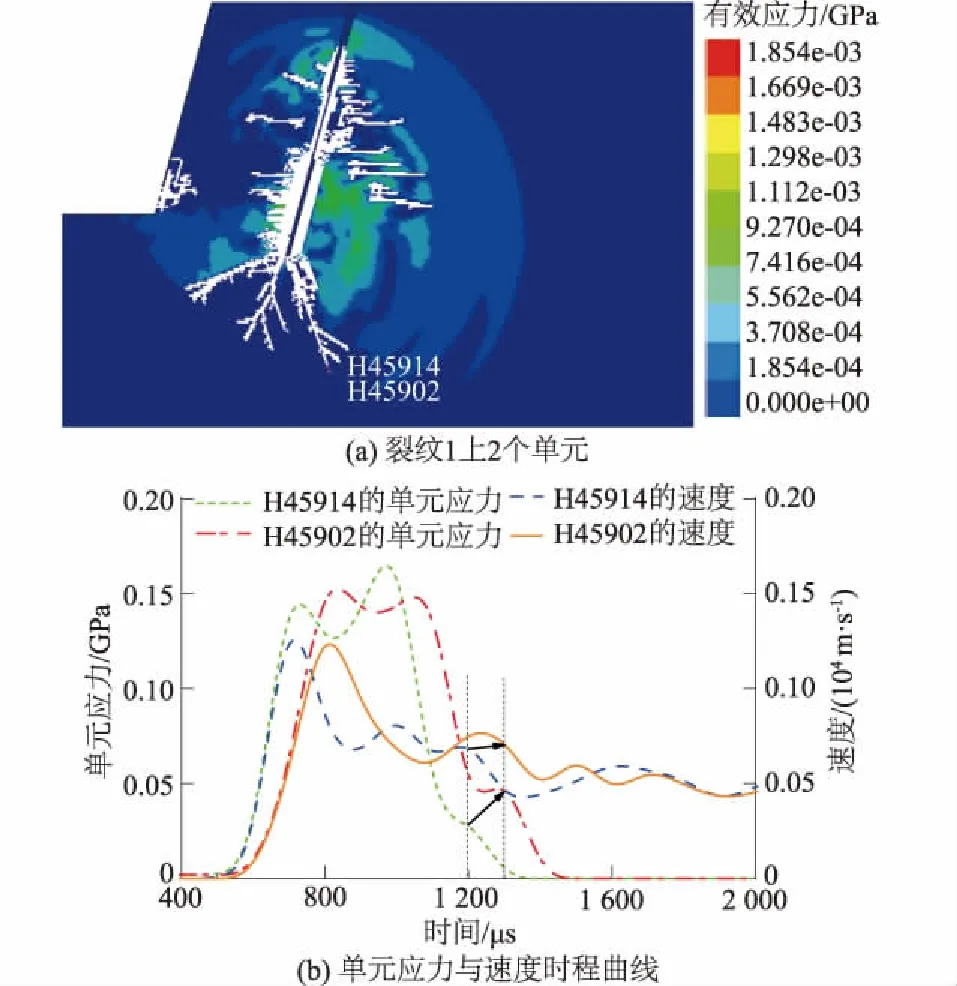
图6 裂纹1上单元时程分析

图7 裂纹2上单元时程分析

在右侧裂纹(裂纹2)依次选取单元为H63098、H63101，位置如图7(a)；分别作出两单元的应力与速度时程曲线，如图7(b)；单元H63098在1 200 μs时为裂纹2尖端，单元应力为0.234 GPa，速度为0.156×104m/s；1 300 μs时裂纹尖端扩展到单元H63101处，单元应力为0.227 GPa，速度为0.115×104m/s。经计算，随时间增加裂纹2的两单元间应力减小2.99%，速度减小26.28%。

在左侧裂纹(裂纹3)选取单元为H12469、H12474，位置如图8(a)；分别作出两单元的应力与速度时程曲线，如图8(b)；单元H12469在900 μs时为裂纹3尖端，单元应力为0.126 GPa，速度为0.114×104m/s；1 300 μs时裂纹尖端扩展到单元H12474处，单元应力为0.174 GPa，速度为0.098×104m/s。经计算，随时间增加裂纹3的两单元间应力增大38.10%，速度减小14.04%。

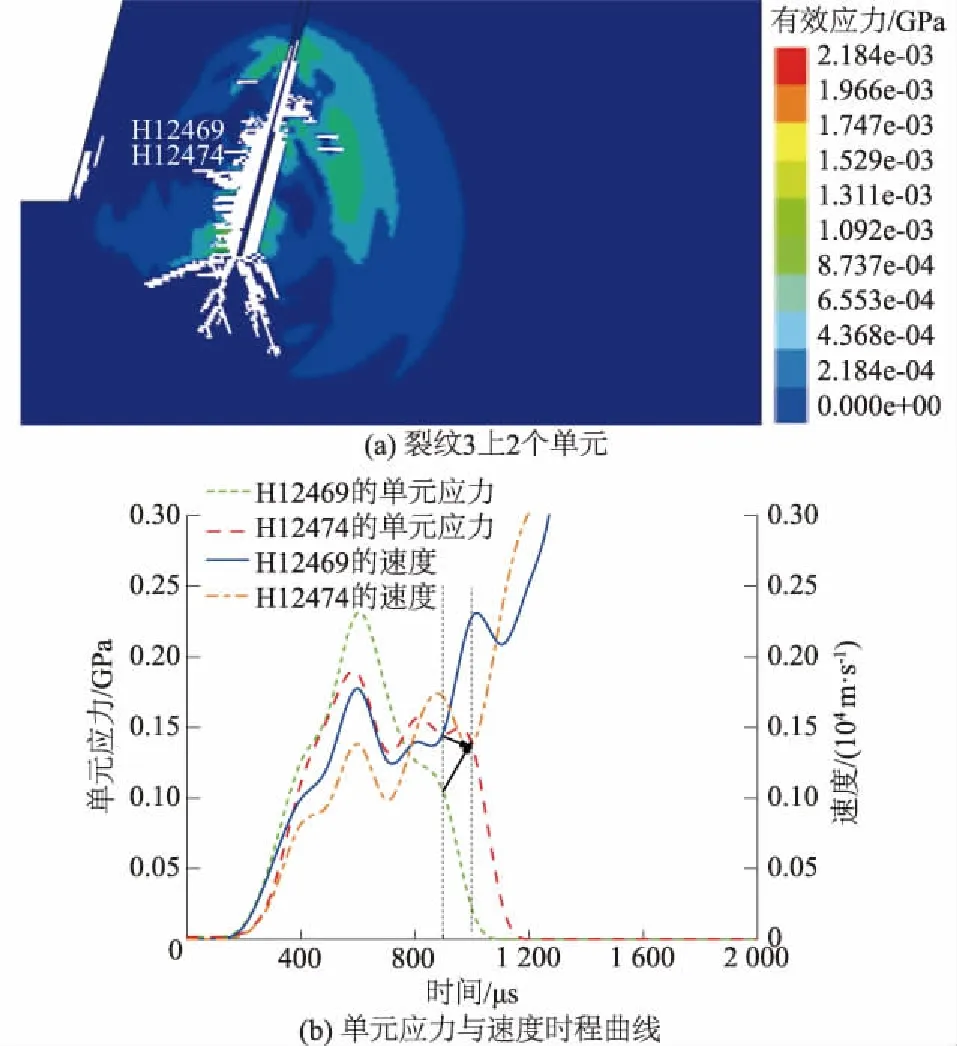
图8 裂纹3上单元时程分析

通过裂纹图与时程曲线综合分析发现：

(1)药柱下侧裂纹1，裂纹尖端处应力变化率是速度变化率的23.7倍，表明在爆破过程中药柱下侧的岩体对应力波能量的消耗较多，裂纹尖端的速度变化率较小，导致裂纹以较细窄状态在岩体中延伸。

(2)药柱右侧裂纹2，裂纹尖端处速度变化率是应力变化率的8.77倍，即单元合成速度均较大，裂纹以扩宽状态延伸，能量主要消耗在裂纹尖端扩宽阶段但降低了裂纹延伸长度。

(3)药柱左侧裂纹3上单元的应力与速度变化率介于裂纹1和裂纹2之间。由于靠近边坡自由面，在爆破过程中岩体受复杂的多方向应力波动态作用以及爆生气体的准静态作用，初始裂纹、层裂裂纹、径向裂纹相互贯通，或产生环向裂纹。因此自由面附近的岩体裂纹密度大于其他位置，岩体得到充分破坏从而得到较理想爆破效果。

为验证结果的可靠性，分别在上述3条裂纹上连续选取裂纹扩展路径上的3个裂纹尖端单元，进行应力与速度时程分析。得到数据如表3—表5所示(负值表示减小)。

表3 裂纹1单元应力与速度变化

注：单元应力和速度的初末变化率分别为2.04%，15.68%。

表4 裂纹2单元应力与速度变化

注：单元应力和速度的初末变化率分别为-4.70%，-13.46%。

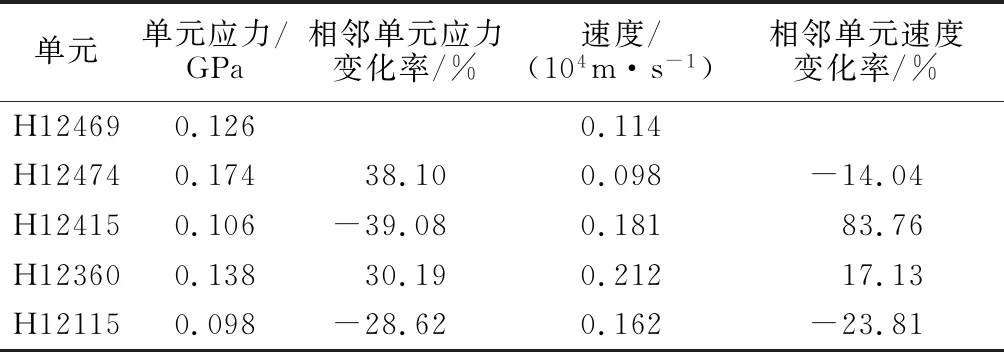
表5 裂纹3单元应力与速度变化

注：单元应力和速度的初末变化率分别为-21.83%，42.11%。

分别由裂纹1,2,3上的单元应力与速度初末变化率求平均变化率，可得裂纹1、裂纹2、裂纹3的平均应力变化率分别为32.61%,14.51%,34.00%。裂纹1、裂纹2、裂纹3的平均速度变化率分别为12.42%,21.88%,34.58%。

裂纹1的裂纹尖端应力变化率较速度变化率大，裂纹2的裂纹尖端速度变化率较应力变化率大，裂纹3的裂纹尖端应力变化率与速度变化率基本接近。这与前面的分析结果较吻合，得到边坡爆破过程中不同位置处的裂纹尖端由于受到不同比例的应力与速度状态，从而产生不同的裂纹扩展形态。同时，本文下部裂纹1与右部裂纹2的平均应力变化率之比约为2.25，基于不同药包的应力衰减系数公式(式(10)和式(11)，球状药包爆破应力衰减系数为柱状药包应力衰减系数的2倍，模拟结果与应力衰减系数之比基本吻合。

4 结 论

(1)利用LS-DYNA软件模拟边坡爆破裂纹扩展模型，模拟出岩体在爆破过程中先后受到爆轰波(冲击波与应力波)的动态作用及爆生气体的气楔准静态作用。爆轰波直接作用并传播于岩体中，对岩体的结构失稳开裂起到主要作用；爆生气体通过气楔直接作用于裂纹内部，进一步促进了裂纹的扩展。

(2)通过选取3条不同位置裂纹上的单元进行有效应力与速度时程分析，以逐时差法分别对比了裂纹尖端扩展路径上单元的有效应力与合速度的变化。在裂纹尖端单元处，当平均应力变化率大于平均速度变化率时，裂纹扩展沿原方向(轴向)破裂较为显著；当平均应力变化率小于平均速度变化率时，裂纹扩展以径向扩张较为显著；当平均应力变化率与平均速度变化率近似时，裂纹扩展既有延伸又有延展，为最理想裂纹扩展形态且有利于岩石破裂。

(3)在理想岩体条件下，球状药包爆破应力衰减率约为柱状药包爆破应力衰减率的2倍，本文的平均应力变化率模拟结果约为2.25倍，二者基本吻合。

(4)爆破产生的裂纹分布也是岩体破碎成块的表现，破碎大块主要来源于边坡坡脚、炸药与堵塞物接触面两侧围岩以及台阶顶部自由面处，上段填塞与自由面处由应力波反射拉伸使得局部压力叠加而形成大块，下段坡脚处由于结构非连续性导致岩体阻抗较大，也会有局部大块现象。