基于EEMD与SE的IPSO-LSSVM模型在坝肩边坡变形预测中的应用

(成都理工大学 地质灾害防治与地质环境保护国家重点实验室，成都 610059)

1 研究背景

随着我国经济的蓬勃发展和科技的快速进步，水利工程建设的规模和数量在不断扩大和增多，大坝能否安全运行关系着亿万人民的生命和财产安全。然而，坝肩边坡变形受库水位、温度、时效和降雨等多种外部因素的影响，呈现出随机性和非线性，预测难度颇大，越来越受到国内外学者的重视[1]。

坝肩边坡变形是大坝安全监测的重要组成部分，传统的预测方法主要有：多元线性回归法、灰色理论法、差分进化法和单一神经网络法等[2]。但这些方法都有明显的缺陷，预测效果并不好[3]。目前的研究阶段主要思想是基于将变形时间序列视作一条复杂的信号，将信号分解分析再合并，前人已取得了一定的成果。李捷斌等[4]基于Kalman滤波将变形时间序列进行分解，再分别使用BP神经网络进行训练和预测，取得了较好的预测精度。但Kalman滤波限制条件较为苛刻，当数据发生突变时，会影响算法收敛。李骅锦等[5]提出了一种小波变换与极限学习机耦合的边坡变形预测办法。小波变换克服了Kalman滤波的不足，但是在小波基函数和分解尺度的选取上过于经验化，不易推广。任超等[6]基于经验模态分解(Empirical Mode Decomposition，EMD)，提出名为EMD-GA-WNN的边坡变形预测模型，取得了更高的精度。相较于小波变换，EMD具有更加简单、直观、基于经验和自适应的特点。但需要指出的是，由于信号端点不一定是极值点，基于三次样条插值获得的上下边界包络线可能存在“边界效应”等问题，不易分析出“隐含的”信号变化特征。为了克服以上缺陷，一种名为聚类模态经验分解(Emsemble Empirical Mode Decomposition，EEMD)的新型信号处理方法被提出，并被运用到了边坡变形的预测上[7]。

另一方面，作为支持向量机(Support Vector Machine, SVM)的发展和改进，最小二乘支持向量机(Least Square SVM，LSSVM)采用等式约束来代替不等式约束，不但解决了神经网络隐含层节点数难以确定、易陷入局部极小值和过拟合的问题，还克服了SVM求解速度较慢、鲁棒性不强的缺陷，近些年来得到了广泛关注，并取得了较好的效果。为进一步提高模型预测精度，降低人为选取参数造成的误差，在对LSSVM进行参数寻优时，本文提出了一种具有较强的全局搜索能力的改进型粒子群算法(Improved Particle Swarm Optimization，IPSO)，以提高网络性能。

本文以澜沧江苗尾水电站左岸坝肩边坡上部TPYb2-1和下部TPYb6-1监测点的变形数据为例，基于聚类模态分解、样本熵(Sample Entropy, SE)和改进型粒子群算法优化的最小二乘支持向量机(IPSO-LSSVM)，提出了一种基于EEMD-SE-IPSO-LSSVM耦合模型的坝肩边坡变形预测方法。通过将BPNN(BP神经网络)、RBFNN(RBF神经网络)、LSSVM、EEMD-SE-LSSVM与EEMD-SE-PSO-LSSVM模型预测值进行比较，验证了本文所构建模型的合理性和优越性。

2 理论与方法

2.1 聚类经验模态分解

所谓EMD法，即将任意信号分解为一系列具有不同特征尺度的本征模态函数(Intrinsic Mode Function, IMF)分量和残余分量的一种自适应信号处理方法，其实现步骤参见文献[8]。分解提取的各个IMF分别代表原始信号内包含的一个尺度波动成分，而残余分量通常代表原始信号的趋势[9]。但相关研究[10]表明，由于原始信号间隙性的存在，EMD无法克服模态混叠缺陷，使得IMF物理意义不明确。为此，Wu和Huang[11]提出了一种改进方法——EEMD。该方法的核心是通过引入辅助噪声来消除原时间序列中的间歇现象，再进行多次EMD分解取平均值。EEMD对坝肩边坡变形时间序列的分解步骤如下[12]：

(1)在原始坝肩边坡变形时间序列中加入随机高斯白噪声序列nm(t)，即

xm(t)=x(t)+nm(t) 。

(1)

式中：x(t)为原始序列；xm(t)为加入噪声信号后的待处理的序列；nm(t)的标准差一般取x(t)的0.05～0.5倍[13]，本文取0.2。

(2)对原始坝肩边坡变形时间序列依次加入M个不同但标准差相等的白噪声序列进行重构(M基于算法提出者的建议和本文运算中的经验取100)，基于EMD将重构序列分解成n个IMF分量ci,m(t),i=1,2,…,n，以及一个剩余分量rn,m(t)，最终得到M组不同的IMF分量和残余分量。

(3)分别计算M组IMF分量及剩余分量的均值，并将其作为EEMD分解的最终结果，即：

(2)

(3)

2.2 样本熵

EEMD分解得到的子序列往往数量较多，计算规模较大，不利于模型运用和推广。因此本文使用样本熵[14]对子序列进行重组合并。作为一种量化非线性时间序列的良好工具，样本熵可以快速分辨子序列的复杂度，将复杂度相近的子序列进行合并，在保证精度的前提下，减少计算次数，提升计算时间。相较于近似熵，两者计算原理虽然相似，但样本熵不依赖数据长度，具有更好的一致性且对于丢失的数据不敏感[15]，有效地克服了近似熵的不足。

对于给定的时间序列{x(i)|1≤i≤n}，n为数据个数，构建一个m维矢量X(i)，即X(i)={x(i),x(i+1),…,x(i+m-1)}，其中i=1,2,…,n-m+1。那么序列{x(i)}样本熵可定义为[16]

(4)

n一般在100～5 000之间取值。且当n取有限值时，可以基于下式估计，即

(5)

式中Bm(r)，Bm+1(r)分别为2个序列在相似容限r(r>0)下匹配m个点和m+1个点的概率，其计算公式分别为：

(6)

(7)

(8)

从以上步骤可以看出，SE的取值与m和r的取值有关。相关研究[17]表明，当m=1或2，r=0.1Std～0.25Std(其中Std表示原始时间序列xi的标准差)时样本熵统计特征较为合理。本文取m=2，r=0.2Std。

2.3 最小二乘支持向量机

SVM是一种能较好解决小样本、非线性预测以及高维识别的一种机器学习算法，在各领域应用广泛。但该方法具有运算速度较慢、泛化能力较差等问题制约了它的推广与应用[18]。作为SVM的一种发展和改进，LSSVM将损失函数直接定义为误差平方和，并在优化步骤中用等式约束来代替原有的不等式约束，由此将二次规划问题转化为线性方程组进行求解，有效降低了计算复杂性，加快了求解速度[19]。

设原始坝肩边坡变形时间序列为{x(i)|1≤i≤n}，n为监测期数，选取前m期构建坝肩边坡变形训练集D={(xi,yi)|i=1,2,…,m}，其中，xi∈Rd是输入变量，d为输入变量的维数，yi∈Rd为输出向量的期望值。利用非线性映射φ(x)将输入变量映射到高维特征空间，构建LSSVM的回归函数，即

f(x)=ωTφ(x)+b。

(9)

式中：ω为特征空间的权向量;b为偏差量。基于文献[5]提到的LSSVM的基本原理，回归函数的表达式可转化为

(10)

式中K为满足Mercer条件的核函数，本文选取的核函数为径向基核函数(Radial Basis Function，RBF)，即

(11)

2.4 IPSO-LSSVM

令RBF作为核函数时，LSSVM需要优化的参数有2个：正则化参数γ和核参数σ2。而模型参数选取适当与否，决定了模型性能的好坏。为此，本文提出了一种以粒子群算法(Particle Swarm Optimization，PSO)为基础的，并结合“多样性度量指标控制种群特征”[20]思路的改进粒子群优化算法(IPSO)。该种改进型优化算法通过引入“平均粒距D(t)”和“适应度方差Vfitness”2个概念，改进了PSO容易发生早熟、收敛速度慢、后期搜索性能和个体寻优能力降低的不足，对网络性能有较大提升，其具体改进主要体现有：

(1) 在粒子种群初始化阶段，为保证有限个粒子能均匀分布在整个解空间，通过设置平均粒距D(t)，以避免陷入局部最优解。其定义为

(12)

D(t)越小，表示种群越集中，反之则表示种群越分散。计算前设置阈值μ，使得D(t)≥μ恒成立，以保证算法尽可能地使得粒子的轨迹遍历搜索区间。

(2) 在算法寻优搜索后期，为避免陷入局部极值点，通过增加设定适应度方差Vfitness，引导粒子改变位置，以保持种群活力提高全局寻优能力。其定义为

(13)

式中：m为种群粒子数目；f为归一化定标因子，用来限制Vfitness的大小，计算公式为

(14)

Vfitness越小，表示种群中粒子的聚集程度越大，反之则表示聚集程度越小。随着迭代次数的增加，种群中粒子的适应度会越来越接近，就会越来越小。计算前设置阈值δ，当Vfitness<δ时，判定算法进入后期搜索阶段。

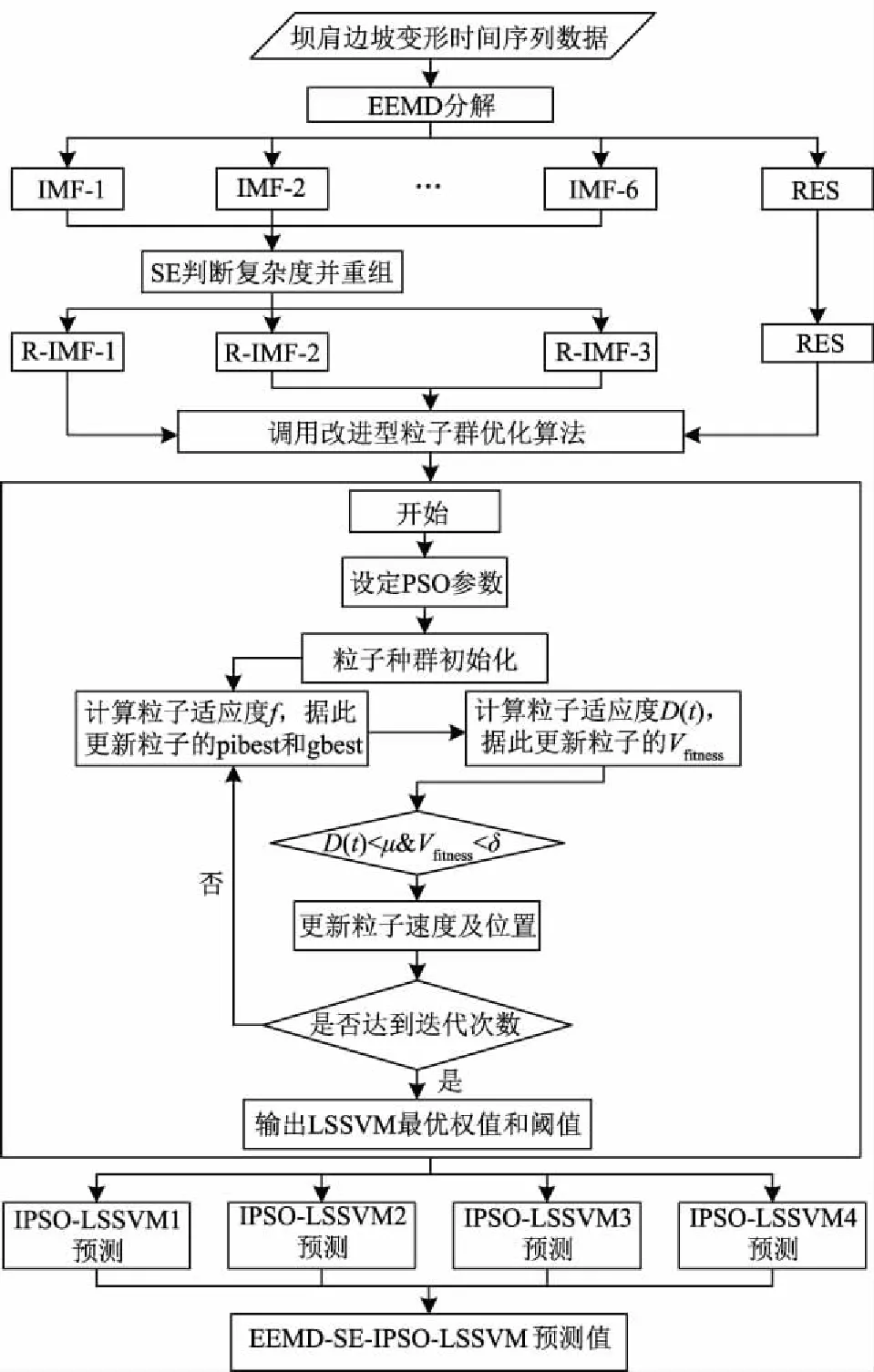
图1 基于聚类经验模态分解与样本熵的IPSO-LSSVM耦合模型流程

2.5 EEMD-SE-IPSO-LSSVM

综上所述，针对传统LSSVM参数不易确定且单一预测模型预测精度不高的问题，提出了一种基于EEMD与SE的IPSO-LSSVM的坝肩边坡变形位移预测耦合模型，其具体流程如图1所示。

3 工程应用

苗尾水电站位于云南省大理州云龙县旧州镇水井村附近，是澜沧江上游河段水电开发规划“一库七级”的第七级，设计坝高138 m，坝顶高程1 422 m，水库正常蓄水位1 408 m，相应库容7.01亿m3，总装机容量120万kW[21]。为保证大坝正常安全运转，在大坝各处布置了多个变形监测装置。其中在左岸坝肩边坡上共设置了上、中、下3部分，共计17个位移监测点，如图2所示。本文选取变形较为剧烈的下部TPYb6-1监测点作为研究对象，将2016年12月至2017年5月共计64期监测数据作为训练样本(验证样本基于“留一法”交叉验证方式生成得到)，2017年6—7月共计20期作为测试样本。应用EEMD-SE-IPSO-LSSVM模型进行训练和预测，并建立相应的BPNN、RBFNN、LSSVM、EEMD-SE-LSSVM和EEMD-SE-PSO-LSSVM，以作对比。

图2 苗尾水电站左岸坝肩变形监测点布置示意图

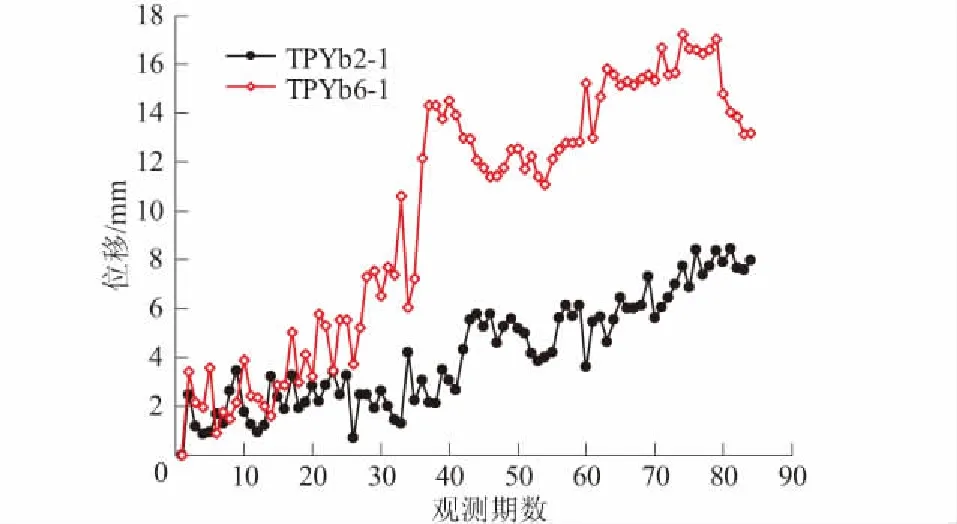
图3 坝肩边坡变形位移时间序列

3.1 坝肩边坡变形预测

如图3所示，坝肩边坡变形极其不稳定、波动性较强，表现出明显的非线性和高度随机性的特点。采用EEMD对位移监测数据进行分解处理，得到6个IMF子序列和一个残余RES子序列，再计算各子序列的SE值，最终的结果如图4所示。

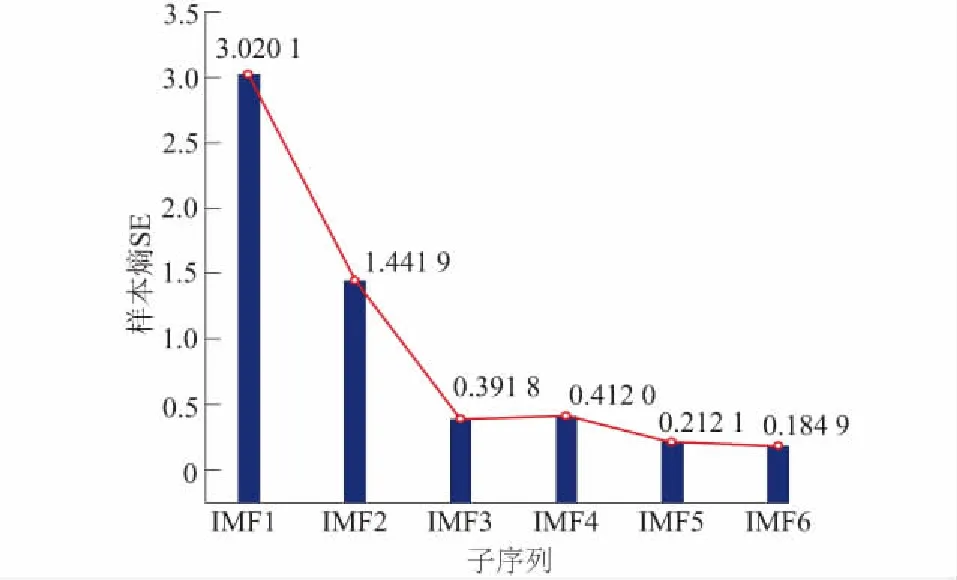
图4 各子序列的样本熵

SE值越接近则表明相应的子序列复杂度越接近。由表1可知，IMF3和IMF4的SE值较为接近，IMF5和IMF6的SE值趋于相同，为减少模型计算规模，将它们进行合并。最终合并重构的新子序列如图5所示，各新子序列的方差及方差贡献率如表1所示。

图5 基于EEMD-SE重构的子序列

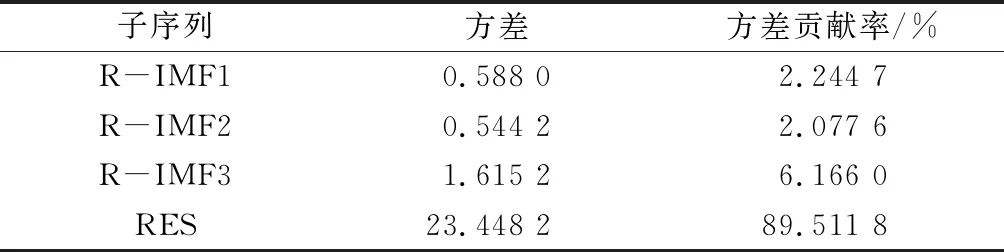
表1 新子序列的方差及方差贡献率

分别对R-IMF1、R-IMF2、R-IMF3和RES建立IPSO-LSSVM预测模型，设置粒子群规模sizepop=30，最大进化代数为maxgan=100，学习因子c1=1.5，c2=1.7，初始惯性权重wini=1，最终惯性权重wend=0.01，按线性递减，平均粒距阈值μ=0.001，适应度方差阈值δ=0.01，粒子向量维数d等于输入因子个数。最终，各模型的输入因子和基于IPSO搜索得到的优化参数值见表2。将各子序列的预测结果依次叠加，得到模型最终的预测结果(见图6)。

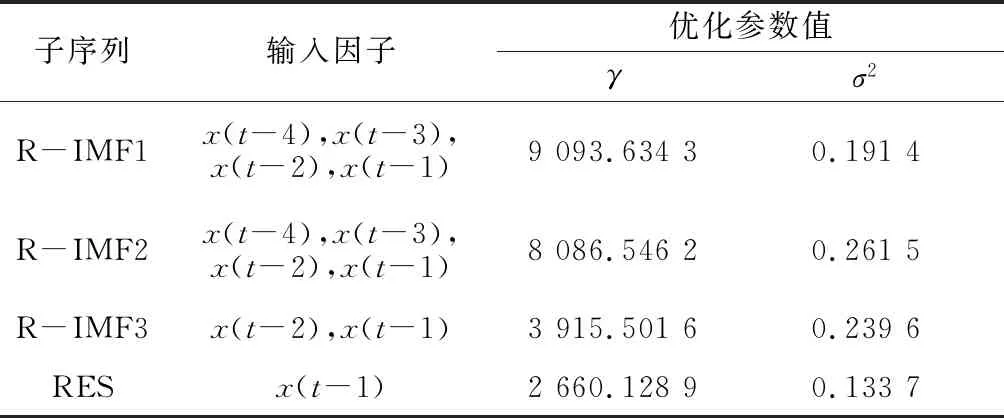
表2 各模型输入因子和参数设置

图6 各子序列实际值与模型预测值比较

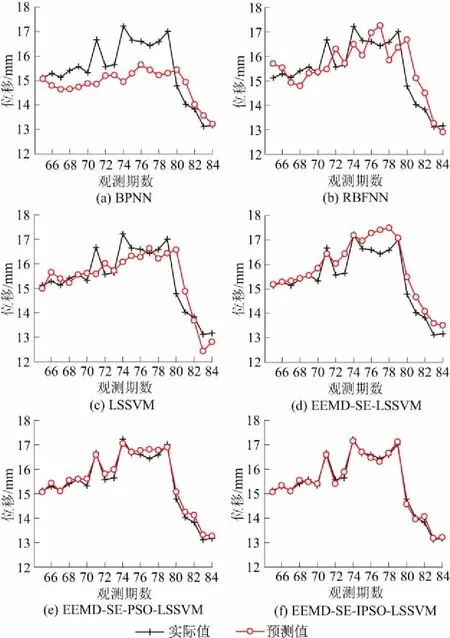
图7 TPYb6-1监测点各模型预测结果

为验证本文模型的准确性和优越性，另采用BPNN、RBFNN、LSSVM、EEMD-SE-LSSVM和EEMD-SE-PSO-LSSVM对样本进行分析预测，各模型的预测结果如图7所示。为进一步验证模型的稳定性与通用性，选取左肩坝上部TPYb2-1监测点变形数据构建预测模型，最终的预测结果如图8所示。

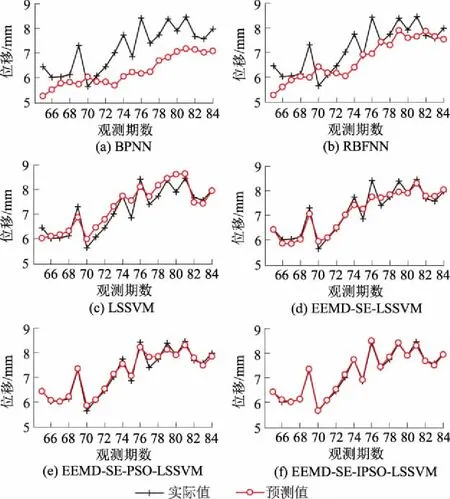
图8 TPYb2-1监测点各模型预测结果

3.2 预测结果分析

为量化各模型之间的可靠性与准确性，本文采用均方根误差(RMSE)、平均绝对百分误差(MAPE)和拟合优度(R2)作为衡量误差精度的标注，计算公式为：

(15)

(16)

(17)

表3 各模型预测效果对比

注：1-6号模型分别为BPNN、RBFNN、LSSVM、EEMD-SE-LSSVM、EEMD-SE-PSO-LSSVM和EEMD-SE-IPSO-LSSVM。

由表3可见，在未进行EEMD-SE重构的单一神经网络模型中，模型3预测效果最好，优于模型1和模型2，说明了模型3性能的优越性。接着基于模型3和EEMD-SE重构的3个耦合模型与单一神经网络模型进行对比，发现在计算精度上模型4、模型5和模型6具有显著优势，测试样本的误差评价参数RMSE和MAPE显著均小于前三者，R2也相对更趋近于1。在这3种耦合模型中，使用了标准PSO的模型5和使用了IPSO的模型6，较未使用粒子群算法的模型4，TPYb6-1测试样本RMSE分别降低了0.290 7和0.369 0，MAPE分别降低了0.755 4%和1.600 7%，R2值也分别提高了0.053 3和0.065 8。模型误差有较大程度的减小，TPYb2-1测试样本的预测结果也大致相同，凸显了粒子群算法在参数寻优中的重要作用。最后将模型5和模型6进行比较，发现IPSO寻优能力比标准PSO更强，模型6的精度比模型5更高。模型在TPYb2-1和TPYb6-1预测值与对应实际值的R2分别达到了0.985 1和0.986 2，体现了该模型通用性好和准确性高的特点。但由于算法结构复杂程度的提升，模型用时有不可避免的增加，但与精度提升相比是值得的。

4 结 论

针对坝肩边坡变形时间序列的高度随机性和非平稳特征，本文基于EEMD、SE和IPSO-LSSVM，提出了一种EEMD-SE-IPSO-LSSVM坝肩边坡变形预测模型，通过对澜沧江苗尾水电站左岸坝肩边坡上部TPYb2-1和下部TPYb6-1监测点的变形数据进行预测分析，得到如下结论：

(1)运用EEMD和SE相结合的坝肩边坡位移时间序列分解方法，将原始序列分解成一组复杂度差异明显的新位移变形子序列，有效克服了传统分解方法人为主观、信息丢失和计算规模大的不足。为原始坝肩边坡位移时间序列的合理分解提供了新的思路与手段。

(2)对新位移变形子序列分别构建LSSVM模型进行训练和预测，并使用一种具有较强的全局搜索能力的IPSO对每个模型进行参数寻优，进一步提高了预测结果的准确性。

(3)最终的计算结果表明，本文提出的EEMD-SE-IPSO-LSSVM耦合模型的R2、RMSE和MAPE均优于BPNN、RBFNN、LSSVM、EEMD-SE-LSSVM和EEMD-SE-PSO-LSSVM模型，是一种有效的坝肩边坡变形预测新方法。