基于声像法非对称型混响室内壁入射声能角度分布的模拟

崔素瑜，穆瑞林, ，闻思梦，衣继钊

(1. 天津科技大学机械工程学院，天津 300222； 2. 天津市轻工与食品工程机械装备集成设计与在线监控重点实验室，天津 300222)

在声学领域，通常利用混响室测定材料的吸声系数与隔声性能[1-4]．现代标准混响室法测量的基础是假设它为完全扩散声场．实际上，其内部声场并非完全扩散声场．早在20 世纪中叶就证实了混响室内各点的声能密度并不相等．随后，Waterhouse[5]的调查也证实了这一点．

近年来，孙海涛等[6]利用双通道测量技术对声学缩尺模型进行测量，得到室内成套声学参数，但此法主要用于声场不均匀度的判断．蔡铭等[7]通过结合室内空间剖分的声线跟踪法对室内声场进行预测，较之传统的声线跟踪法，计算效率显著提高．此外，王海涛等[8]提出的边界无网格模型，对任意粗糙表面形状散射体的散射性质进行估计，提高了室内声场分布准确度．为了增加混响室内的扩散程度，Bradley 等[9]对陶器贴片在3 个不同混响室内造成的散射情况进行实验调查；随后，设计了一款有悬挂反射板的小型混响箱，并通过最大吸声系数、衰减率标准偏差等对其性能进行评价[10-11]．郭莹等[12]在镜像源法上进行改进而得基于变换频域和反射系数的镜像源法，得到了能量衰减曲线和混响时间．而对于混响室内壁入射声能角度分布情况的研究却很少．

Kang 等[13]通过音线法模拟了混响室内壁入射声能角度分布情况，并提出了高斯分布．Jeong[14]通过音束法模拟了混响室内壁入射声能角度分布情况．由于音线法与音束法随着传播时间的变化，音线或音束会产生分散现象，造成声能空间的不连续性．特别是在混响室这样的高反射空间内，经过多次反射后，音线(音束)的间距变大，从而导致了声能的遗漏与特定角度声能的集中，造成模拟误差．

相比于以上两种研究方法，声像法可以解决以上问题．对于只有简单反射平面的混响室，声像法可以进行比较精确的声像预估．由于声像法不存在波的干涉和扩散反射，所以可以获得最大限度的声像数，真实地反映出混响室内壁入射声能角度分布情况．

1 声像法原理

假设声源点S 发出脉冲声波，利用声像法求出各平面声像点I，之后与接收点R 连线求出交点C，即声波在此点发生了反射，进行转向，如图1 所示，其中i＝1，2，3，…．

图1 声像法原理 Fig. 1 Principle of sound image method

1.1 声像点模拟

声像法主要是利用镜面反射的原理，通过声源与反射面构成的三棱锥体积求出高度，然后等于声像与声源点间距离的一半求出声像点，从而得到声波的传播路径．假设反射平面方程AX+BY+CZ+D＝0，已知面上三点(Xa，Ya，Za)(a＝1，2，3)，可知

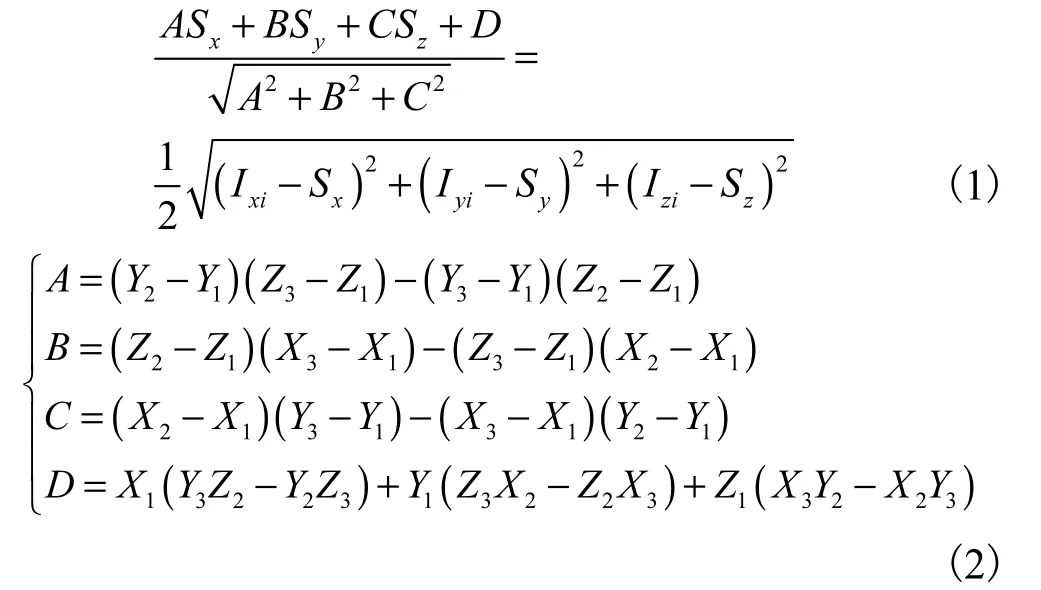
点(Ixi，Iyi，Izi)是点(Ix(i-1)，Iy(i-1)，Iz(i-1))关于反射面Fi的声像点，所以声像点的坐标为

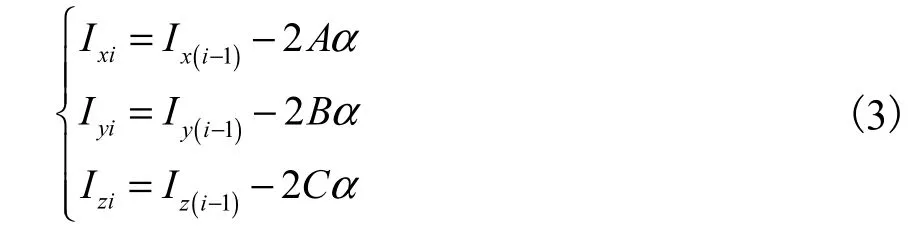
其中α＝(AIx(i-1)+BIy(i-1)+CIz(i-1)+D)/(A2+B2+C2).利用公式(4)判断声像点是否合格

若K＝0，求出的声像点在反射面上，不合格．若K＞0，反射面Fi的声像点在室内，不合格．若K＜0，声像点在室外，合格．

1.2 反射路径模拟

利用式(5)判断声像点与接收点是否为同一点

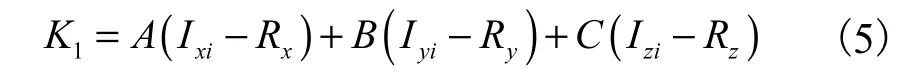
若K1≠0，声像点和接收点不是同一点，之后将声像点和接收点相连，会与反射面产生交点(Cxi，Cyi，Czi)．求得

利用式(7)、式(8)判断声像点、接收点、交点三点是否共线．

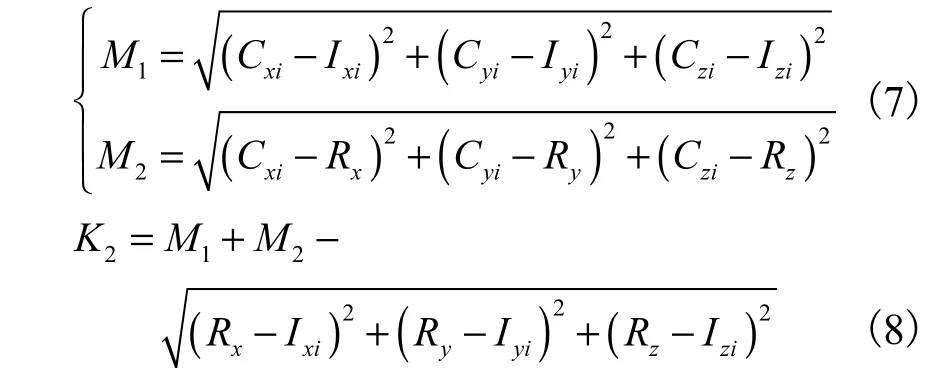
若K2＝0，说明三点共线．

已知反射面法向量n＝(A，B，C)，方向指向室内．按顺序逆时针依次选取反射面的两个相邻顶点，与交点组成一个平面，利用公式(9)求出其法向量(NX，NY，NZ)

与反射面的向量进行点乘求得SC

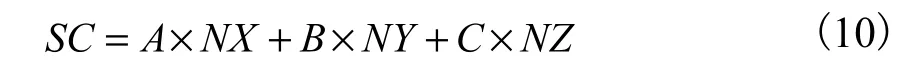
若求得的SC 均大于等于0，那么可确定交点是在面内并且在面上，反射路径合格．

1.3 声能与入射角度的计算

已知声源点到接收点的距离为u0，声波经过多次反射进入接收点的总传播距离为u．由于声能与传播距离的平方成反比，因此归一化处理声能E 可用公式(11)表示

直接到达声的时间、能量分别定义为t0＝0 s， E0＝1．声能入射角度如图2 中θ 所示，即调查平面法向量与入射声能之间的夹角，可由公式(12)计算：

其中(Rx+0.1，Ry，Rz)设为(X0，Y0，Z0)．

图2 入射声能角度分布统计模型 Fig. 2 Statistical model of directional distribution of incident acoustic energy

1.4 模拟流程

非对称型混响室内壁入射声能角度分布情况的模拟研究是利用声像法进行的．模拟程序分为两大部分，一是通过声像法原理模拟所有声像坐标与能量，二是基于球面统计各入射角度归一化后的声能，具体程序模拟流程如图3 所示．通过visual studio 2012 的fortran 语言编辑器实现了该程序的编制．对于只有简单反射平面的混响室，声像法可以进行比较精确的声像预估；而对于有着复杂扩散体的混响室，模拟计算时间会大幅增加．

图3 模拟流程图 Fig. 3 The flowchart of simulation

2 模拟设置

混响室结构如图4 所示，由7 个平面组成，其中位于YZ 平面上的面为调查平面．设置两个声源点S1(1.06，0.2，0.2)与S2(1.06，1.632，0.2)．

图4 混响室结构图 Fig. 4 Structure of reverberation chamber

在调查平面上，以间隔0.1 m 设置接收点，如图5 所示．

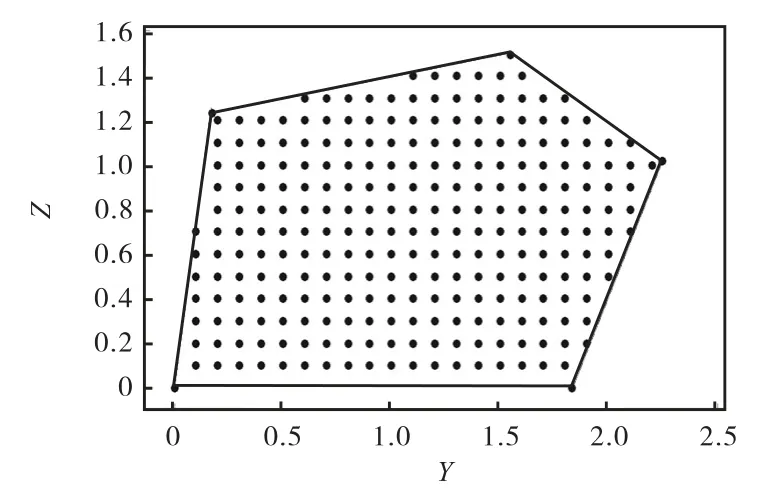
图5 接收点布置图 Fig. 5 Locations of receiving points

将混响室各个内壁面分割成若干个三角形，计算出所有三角形的面积，相加即可求出混响室表面积．另外，分割后的三角形若能与坐标系原点(0，0，0)构成三棱锥，可求出所有三棱锥的体积，相加可得混响室体积．

3 模拟结果与分析

在模拟声波传输、汇总入射声能角度分布情况的过程中，随着时间和反射次数的增加，声能会不断减小．图6 表示了某一接收点15 次反射内射入的归一化后的声能与时间，可以发现第15 次反射及60 ms以上的归一化后的声能已小于0.001．因此，为了节省运算时间，统计有效时间设为100 ms，模拟反射次数设为15 次．通过声像法模拟出进入每个接收点的声能大小、到达时间与入射角度，以每个接收点处声能最大值对各自声能进行归一化处理．之后按照角度大小进行排序，并以1°为单位，将对应的归一化后的声能求和，再除以相应球面面积(球的半径R＝1)，则可得到相应角度的声能密度，再找出0°～90°中声能密度最大值，对各自声能密度进行归一化处理．

图6 一接收点15次反射内射入的声能及其时间 Fig. 6 Incident acoustic energy and time of a single receiving point in 15 reflections

经移动平均处理后，入射声能角度分布结果如图7 所示．

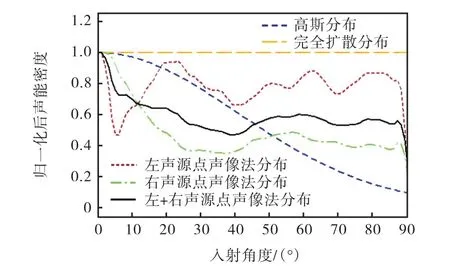
图7 入射声能角度分布模拟结果 Fig. 7 Simulated results of directional distribution of incident acoustic energy

模拟结果表明：入射声能集中分布在0°～20°，在20°～87°区间变化趋于平缓．87°之后迅速下降至0°．而该图中86°～87°数值上升是由于移动平均处理所致．

4 结 论

利用声像法，对以调查平面几何中心为球心的球面上的入射声能角度的分布进行模拟计算．模拟结果表明：非对称型混响室内壁入射声能主要分布在0°～20°，在20°～87°区间变化趋于平缓．87°之后迅速下降至0°，与已提出的完全扩散分布、高斯分布完全不同．根据声像法模拟出的声能入射角度分布曲线更加趋近于真实反射状态．