制定诊断标准 实施精准矫治

徐祯 俞翠华

摘 要：制定诊断标准，使诊断技术化，带动矫治的精准化，是教学中非常迫切、紧要的问题.通过测试结果的分类定量统计和对学生的访谈，对照诊断标准，诊断出学生可能出现的学习障碍，给出相应的矫治策略.在矫治后对接反馈性测试，保证矫治过程有目标、有措施、有激励、有成效.实践证明，这样的矫治精准、及时、有效.

关键词：诊断;测试;访谈;标准;矫治;反馈

文章编号：1008-4134（2019）21-0007 中图分类号：G633.7 文献标识码：B

作者简介：徐祯（1971-），女，浙江金华人，本科，浙江省特级教师，研究方向：对学生物理学习的困难诊断及矫治策略;

俞翠华（1980-），女，浙江绍兴人，本科，中学一级教师，研究方向：互学与诊学的实践研究.

毫无疑问，诊断越准确，矫治越精准.如何采用多种方法，使诊断技术化，从而带动矫治的精准化，是教学中非常迫切、紧要的问题.集体测试是教学质量检测的传统手段，也是学习困难诊断的重要依据.测试结果的分类定量统计，是对班级或年级的整体诊断，这样的统计与分析对整体情况的诊治有定量的优点，但对个体的学习诊断则过于宽泛和模糊.因此，还需要对每个学生的相关数据进行分析，再结合访谈，引导学生的出声思维，在此基础上给出矫治策略，最后进行矫治后的反馈测试，既检验矫治成果、也形成二次诊断，激发、推动学生的学力提升.对全班运用测试诊断具有定向、定人、定量、定靶的作用，集体诊断与个别访谈诊断同步进行，点面结合，使矫治更为精准.

1 诊断测试先行

诊断性测试是为诊断学生在学习上的困难而编制的一种测验.诊断性试题编制应具有诊断细目表，针对哪些问题，知识的漏洞抑或思维的缺陷，还是程序不规范等等，都可以通过测试加以诊断.一个良好的诊断性测试，必须具有五个特点：（1）包含诊断将要测量的维度目标;（2）有均等测量每一个诊断维度的测题;（3）诊断偏重于发现学习的困难，测量同一基本原理的测题应组合在一起，便于分析和诊断;（4）试题的编制侧重最基本的技能、最重要的思维与最常见的错误;（5）试题难度一般控制在0.75左右.

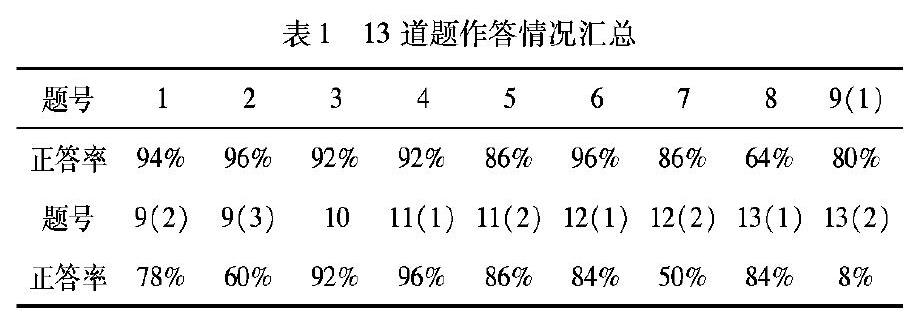
现以“运动学诊断测试”学生作答情况为依据，诊断学生在运动学这一章的学习情况，13道题学生作答的整体情况见表1.

对以上数据进行分析可以发现，1、2、3、4、6、10、11（1）这些题目的正确率相当高，达到 90%以上，绝大多数的学生能够掌握这些知识.而 8、9（3）、12（2）、13（2）这些题目的正确率则低于 65%，说明学生在实验操作和实验数据处理中还存在相当大的困难，在运动学综合和实际情景的应用方面仍存在较大的困难，需要做进一步的分析.而其他题目的正确率在65%—90%之间，说明这些题目所考查的各个概念之间的相互关系在运动学中的应用等内容，学生在学习的过程中还存在一定的困难.总体来说，学生在全部题目中的正确率普遍还是比较高，这说明学生对于运动学的学习存在的困难比较集中，这是学生的集体性诊断结果，它可以指导教师调整教学的重点和方向，但对个体而言，同一题错误对应的原因却各不相同，矫治方法也因人而异，所以还要结合个别访谈，对学生的错误细加诊断.

2 诊断标准制定

人的学习大致遵从相同的认知规律，在学习同一内容时，新手遇到的问题具有共性.本文依据学生学习困难的大量数据，依据表2归纳出学生存在的学习障碍从六个维度去进行诊断.

前概念的干扰障碍主要指先前的生活经验、以往的局部知识带来的新课学习干扰.比如，初中的二力平衡知识，有大量重力等于支持力的实例，在高中学到滑动摩擦力时，就容易想当然地用重力代替正压力，简单粗暴出错;物理模型建构主要指解决实际问题时，忽略次要因素、凸显主要特征的一种模型建构方法.主要分两类：一是研究对象的模型构建;二是物理过程的模型构建.对于实际问题，可以忽略什么或不可以忽略什么都对问题解决有深刻的影响.比如，估算一片树叶下落时间，学生容易将其所受空气阻力视而不见，错当作自由落体运动来处理;物理含义理解障碍主要指学生不顾实际物理过程的合理性，错将数学解等同于物理解，比如刹车问题;结论的条件性障碍是指学生运用规律等同于套用公式，对规律的适用条件和范围不甚了解或视而不见，比如Ff=μFN，只适用于滑动摩擦力的计算，但是学习新手经常错将它用于静摩擦力的计算;对象过程转换障碍主要出现在多物体、多过程的问题情景中，为了便于解决问题，需要简化对象或将物理过程化大为小、分段处理，其中还要考虑各个对象或过程的相互关联;规律公式选取障碍主要指针对具体过程，能够选取合适的规律解决问题，比如，物体做加速度变化的直线运动时，选取运动学规律和牛顿运动定律来处理显然不恰当，这时通常要选用动能定理或其他规律解决问题.

3 分类精准矫治

诊断不是目的.精准矫治才是教学孜孜以求的目标.下面还是以运动学诊断测试为例，重点聚焦个体学习障碍的诊断与矫治.

3.1 物理含義理解障碍

3.1.1 作答及访谈案例

案例1 一辆汽车以10 m/s的速度沿平直公路匀速前进，因故紧急刹车以-0.2 m/s2的加速度前进，则刹车后汽车在1 min内通过的位移为

A.240 m B.250 m C.260 m D.90 m

作答情况显示，20%的同学错选A项.教师进一步访谈的情况如下.

师：能说说你是怎么做的这道题吗？错哪里？

生：做时没有想到50s时已停止运动，用公式x=v0t+12at2计算时，时间应该是50s，而不是60s（说明该学生只是满足于数学解，未从实际过程考虑解的物理含义）.

3.1.2 矫治策略——重视观察思考，培养实践意识

该题看似简单，已知量“相当”明确，却已陷入“刹车陷阱”，对最后的数学运算结果没有从物理的角度进行审视，也就没有因此去进行反馈和校正的过程.在物理学习中，我们需要以数学为工具，但在最后必须分析这个数学解是否就是物理解.对于初涉高中物理的学生而言，还无法自如地从物理含义的角度去理解问题，这种能力的培养无法一蹴而就，需要在生活中，多观察现象，多深入思考，逐步养成实践意识.养成不满足于数学解，经常从实践的合理性角度思考问题的习惯.

3.2 前概念的干扰障碍

3.2.1 作答及访谈案例

案例2 质点做直线运动的v-t图象如图1所示，则

A.在第1 s内质点做变速直线运动

B.在1～3 s内质点做加速度a=-3 m/s2的变速直线运动

C.在2～3 s内质点的运动方向与规定的正方向相反，加速度方向与1～2 s内的加速度方向相同

D.在前3 s内速度的变化量为4 m/s

作答情况显示24%的学生出错，主要问题出在C、D选项.教师访谈情况如下.

师：能说说你是怎么做的这道题吗？

生：开始时认为C、D都对，后来觉得C后半句有问题（反映对加速度的矢量性认识不足或图象意义的不理解），就选了D，其实D选项也不是很理解（反映对速度变化量的矢量性认识不足，初中的学习不涉及矢量运算，学生头脑中并未建构“矢量”观念），所以可以说是蒙的.

3.2.2 矫治策略——主动出击，拉出旧观念

用图象法解题要注意图象的“斜率”“面积”和“截距”的特定意义，要学会“识图”“画图”和“用图”，将学生理解运动图象的困难具体归纳为以下几点：（1）把图象看作轨迹的错误;（2）不通过原点的直线的斜率错误;（3）对面积正、负的忽略，对于面积的迁移能力、综合分析能力、灵活应变能力还较弱;（4）速度变化量的矢量性还不够明确.很多的知识已存储在脑海中多年，而如今却需要去否定它们，而后重塑它们，难度可想而知.学习新观念时，绕不开旧观念，如果只是将新观念建立在旧观念上，表面上看起来好像是习得了新观念，实则不然.当需要在新的情境中运用新观念时，往往会再次暴露错误的旧观念，这反映了错误前概念的顽固性.新课教学中，教师应该通过各种手段，引导学生认识原有观念的局限性或不足，因此，培育完整新观念时，首先需要将错误的旧观念拉出，然后才能被取代.复习阶段，采用苏格拉底问答式，是拉出知识背景深处旧观念的好方法.

3.3 结论的条件性障碍

3.3.1 作答及访谈案例

案例3 下列关于直线运动的认识，其中正确的是

A.匀变速直线运动中，第1s内、第2s内、第3s内位移之比一定为1∶3∶5

B.匀变速直线运动中，第1s末、第2s末、第3s末速度之比可能为1∶2∶3

C.直线运动的物体速度从v1增加到v2，此过程的平均速度为v1+v22

D.匀变速运动的加速度是一个恒量

作答整体统计显示，此题的正答率偏低，特别值得注意的是错选A项的占55%、错选C项的占30%.教师访谈情况如下.

师：你们是如何确定答案的？

生1：我记得（只记得结论，没有理解，不知道结论成立的条件）ABC选项都是对的，所以选了ABCD.

生2：我只能排除A和B，C和D是猜的.

生3：我能确定D一定是正确的（说明对匀变速运动概念有清晰的认识），因为是单选题，只能选D.但其他三项我也不知道具体错在哪里（说明对前面3项推论性质的结论认识模糊，对结论的成立条件茫然不知）.

3.3.2 矫治策略——重视规律理解，培养条件意识

对已知条件不敏感，无法选择最佳运动学公式，对推论性质的结论，只是形成表象的记忆，对结论的适用条件一无所知，这样的知识是死知识，并无用处.高中的物理规律不算多，也并非普遍适用，多数规律还是需要判断条件后才能使用，这是物理学严谨性的体现.特别是运动学中公式还是比较繁杂的，需要推导和梳理，明其物理环境，判其适用条件.矫治教学应该循循善诱，引导学生重温规律的得出过程，加深对规律的理解，在运用规律解决问题的过程中，形成运用规律、结论的条件意识.

3.4 对象过程转换障碍

3.4.1 作答及访谈案例

案例4 有若干相同的小球，从斜面上的某一位置每隔0.1 s无初速地释放小球，在连续释放若干个钢球后，对准斜面上正在滚动的若干小球拍摄到如图2所示的照片，测得AB=15 cm，BC=20 cm，求：

①拍摄照片时B球的速度;

②A球上面还有几个正在滚动的钢球.

典型的作答错误如图3所示.

教師访谈情况如下.

师：你选用了最佳运动学公式，做得不错.但在简单的第2小题的最后一步为什么会出错呢？很可惜啊！

生：主要是第2小题的小球数量的转化上有点蒙了，0.35s与实际情景联系不起来，是应该四舍五入呢，还是应该进位上去（显然，纯数学的观点无法解决全部的物理问题）呢？

3.4.2 矫治策略——重视图景展示，强调找准关联

学生在把求出的时间转化成球的数量时产生了错误，这种转化其实已不是一个纯粹的物理问题.只要具备图景意识，画出示意图，很容易解决问题，即所谓的有图有真相.而这种类似的问题在物理学习中经常碰到，行之有效的应对策略是画出清晰的示意图，找准原过程或原对象与转换后的过程或对象的关联，这个关联主要指时间或空间上的关联.

3.5 物理模型建构障碍

3.5.1 作答及访谈案例

案例5 在一闹市区内，一辆小汽车在平直的公路上以速度vA向东匀速行驶，一位外地游客正由南向北经斑马线上横过马路.汽车司机发现前方有危险（游客正在D处），经0.7 s作出反应，紧急刹车，但仍将步行至B处的游客撞伤，该汽车最终在C处停下.为了清晰了解事故现场，现以如图4示之.为了判断汽车司机是否超速行驶，交警部门派一警车以法定最高速度vm=14 m/s行驶在同一马路的同一地段，在肇事汽车的起始制动点A紧急刹车，经14 m后停下来.在事故现场测得AB=17.5 m，BC=14 m，BD=2.6 m（取g=10 m/s2）.问：

①肇事汽车是否超速行驶？

②游客横过马路的速度大小是多少？

总体的作答得分率只有42%，访谈之后发现各有各的错法，各有各的难处.

师：在这一类实际问题中，你们感到最困难的是什么？

生1：应该是无法在冗长的题目中提取核心的信息，没能把警车的运动与小汽车的运动建立联系，也没找到小汽车的运动与游客的运动之间的联系.

生2：第2小题的解答中无法准确地选择运动学公式，绕了很多弯路，致使数学计算更复杂.

生3：一细节的信息没能准确地提取，在车辆运动时间的换算上出现了失误，忽视了反应时间.

3.5.2 矫治策略——重视抓大放小，强调模型优先

当学生碰到这类涉及实际问题的物理题，往往手足无措，根源在于无法把实际的问题转化为所学的物理模型.比如，这里将游客和汽车简化成质点模型，游客质点的运动模型为匀速直线运动，而汽车质点的运动模型为先在反应时间内做匀速运动，之后做匀减速运动.经历这样的建模过程，剪除旁枝杂蔓，问题得到有效简化.一般而言，物理模型有两类，一类是对象模型、一类是运动模型，不管哪类模型，都需要分析相关因素对问题的影响大小，只有忽略次要因素，才能突出本质特征，从而建立物理模型.形象来说，建立模型就是好好地修理旁枝末节，牢牢抓住主干，只有这样，题目图景才能充分聚焦，趋于清晰.涉及具体情境的问题解决应该重视抓大放小，强调模型优先.

3.6 规律公式选取障碍

3.6.1 作答及访谈案例

案例6 一个做匀加速直线运动的物体，在连续相等的两个时间间隔内，通过的位移分别是24 m和64 m，每一个时间间隔为4 s，求物体运动的初速度和加速度？

作答情况显示一半以上的学生选取规律公式机械作答，解题过程繁琐纠结.针对这一情况，访谈时做了个小调查.

问题1：做运动学的题目时，你比较喜欢

A.仅直接代入基本公式计算

B.公用公式计算

C.先考虑基本公式，不行的话再导出公式

D.先考虑导出公式，不行的话再基本公式

E.同时考虑基本公式和导出公式，尝试不同的解题方法

做运动学的题目时，你比较喜欢采取哪种方式？ 如图5，有36%的学生选择了A“仅直接代入基本公式计算”，说明这部分学生采用的方法单一，不愿意多花功夫去尝试其他方法;有 38%的学生选择了C“先考虑基本公式，不行的话再用导出公式”，这部分学生跟前者差不多，思维比较懒惰.选择E“同时考虑基本公式和导出公式，尝试不同的解题方法”的学生只占了 14%，这部分学生相对其他学生来说对知识的理解更深刻，因为对于运动学这一部分内容来说，只有不断地尝试用多种解题方法去解答，才能更透彻地理解运动学的知识，日后才能够更灵活地运用它来解决问题.

问题2：对运动学的规律和公式，你是

A.能推导出来、能理解、能记住

B.不能推导出来、但能理解、能记住

C.不能推导出来、不能理解、死记硬背能记住它

D.不能推导出来、不能理解、记不住

对于物理学习困难的学生在学习运动学规律时的理解和掌握情况，我们可以通过图6清晰地看出，能够自己推导出来、真正地理解和记住它的学生只有13%，而其他 87%的学生都不能够自己推导出来，清晰地说明了大部分学习困难学生的逻辑思维能力有待提高;有 43%的学生还无法理解运动学规律的真正意义，只能靠死记硬背来记住它，更有 15%的学生不但不能理解，连记都记不住它，说明这半数以上的学习困难学生的理解能力和学习思维能力偏低，有待提高.

3.6.2 矫治策略——养成大局观念，强调规律选取

案例6这个问题，对应的解决方法有6种以上，各种思维路径对应的繁简程度大不相同，甚至可以说有天壤之别.注意到题给条件有位移和相邻相等的时间，首先考虑利用平均速度或相邻相等时间内的位移差解决问题，事实也证明，从这两个角度入手解决问题最为高效迅速.有全局观念的人，做人做事往往站得高、看得远，能够认清方向，能够看清事物的全局和事情的来龙去脉，从事物的关键处着手解决问题，不至于走弯路.解决较为综合的物理问题时，需要站在全局谋局部，弄清每一个规律的来龙去脉，根据不同的模型特征和具体条件，选取合适的规律解决问题.应该特别注意的是，这样的全局观念并不能寄希望于学生自发转变，需要教师点拨与学生反思互通关联起来，才能达到满意效果.

4 矫治测试跟进

矫治之后，立即进行反馈性测试.这样做的目的是让学生有目标地学习，同时制定相应的激励措施，助力有效矫治.这一环节的关键点在于“矫治什么、反馈什么”，精准对接.因此，反馈性测试命题要根据诊断目标维度制定細目表，与诊断测试无缝对接.表3是运动学反馈和诊学测试的错因诊断分析.

通过测试初步诊断出学生知识的薄弱点，通过和学生的对话，更深入地了解学生在方法选择和操作中的各个环节，最后聚集到两个问题，准确锁定学生的困难，在此基础之上，编写出对应的题目，进行反馈性测试.反馈性测试也是重要的反馈手段之一，它与诊断性测试前后关联.要达到好的效果，诊断性测试之后，需要对学生出现的错误实施个别诊断，给出矫正措施，学生按矫治方案完成纠错改错的工作，这时反馈性测试及时跟进.诊断性测试错什么，对症对因就矫治什么，反馈性测试就测什么，即“错什么、治什么，就反馈什么”.因此，反馈性测试的内容与诊断性测试的结果，有强烈的相关性，它必须反映学生的典型错误，两次测试的错因诊断的对照分析见表3.诊断性测试的难度系数一般控制在0.75，而反馈性测试卷的难度系数一般控制在0.85左右.反馈性测试成绩可以覆盖原来的诊断性测试成绩，这是激励措施.参加反馈性测试的学生，心中有目标，内在的学习动力得到激发.因此，矫治阶段特别努力，测试反映对知识的掌握程度有明显提升，学生的自信心增强、课堂精神面貌焕然一新.

5 结束语

诊断应该为精准矫治服务.从教学实践总结、提炼出技术化的诊断标准，再将之用于实践，使得学习诊断脱离算命式的模糊描述，使诊断有据可依，教师操作的可行性更强，技术化的特征也便于其他教师批量复制诊断方法.诊断性测试的集体诊断与个体诊断相结合，便于师生在全局参照的环境下考察个体学习困难.辅之以相应的矫治措施，进行矫治后的反馈测试，使得矫治过程有目标、有措施、有激励、有成效.实践证明，这样的矫治精准、及时、有效，值得推广.

参考文献：

[1]安娜，杨香玲. 测试对教学的反拨作用[J]. 教育现代化，2018，5（01）：279-281.

[2]徐传功.“物质的量”专题习题解题错因分析及对策研究[D].上海：华东师范大学，2014.

[3]徐光建. 高一物理学习困难认知诊断测验的编制[D].南昌：江西师范大学，2011.

[4]高颖. 流程图法在结构设计原理教学中的应用[J]. 中国建材科技，2016，01（25）：87-89.

[5]牛卫华，张梅玲.西方有关学习困难问题研究的新进展[J].心理科学，2000，23（3）： 357-358.

（收稿日期：2019-08-08）