温度影响下基于频率协整余量的桥梁损伤识别

(福建江夏学院 工程学院，福建 福州 350108)

虽然频率能反映结构的性能状态，但在实际工程应用中，由于外界环境和运营情况的影响，测量得到的结构振动频率包含了多种成分，无法直接用于结构损伤识别，阻碍了它在实际工程应用中的推广。为此，从实测数据中分离非结构自身变化引起的伪信号成为国际上研究的热点和难点。只有解决了这个问题，基于频率的结构损伤识别在实际结构健康监测中才有意义。目前，学者们提出了主成分分析[1]、神经网络[2]和状态空间重构[3]等方法，这类方法在一定程度上都能有效地分离外界因素的影响，得到较为准确的频率，但在数据处理中较为繁琐，在噪声干扰较大的情况下，缺乏稳定性，在实际工程应用中还存在较多的问题[4-5]。

基于此，本文引入计量经济学中处理非平稳问题的协整概念，检验结构振动响应是否满足协整的基本条件。将结构正常运营状态下采集的数据作为训练样本，计算得到协整余量，根据统计理论选取协整余量的控制线。以控制线为基准，在后期的监测过程中，若频率的协整余量超过该控制线，表示结构有可能发生损伤；否则结构完好。最后利用自锚式悬索桥数据验证所提方法的有效性和噪声鲁棒性。

1 协整的基本理论

1.1 协整的定义

假设非平稳信号yt经过d阶差分Δdyt=Δ(Δd-1yt)后可变成平稳信号，那么可认为yt是d阶单整的，可记为I(d)。若时间序列未经过差分，自身检测结果就是平稳的，那么可以看成是0阶单整，即为I(0)。如果某一时间序列信号不管经过几次差分，始终无法转化为平稳信号，那么该信号为非单整的。

1.2 协整关系的检验

协整检验的方法主要有Engle-Granger检验(简称EG检验法)和Johansen检验(简称JJ检验法)两种。本文采用EG检验法。

以两个变量的EG检验为例，对其检验过程进行详细说明。若两个时间序列均为0阶单整，则表示其为平稳信号，可直接建立回归模型；若两个时间序列具有相同的单整阶数，则可进一步用EG法检验协整关系是否存在；若两个时间序列单整阶数不一致，则可以确定二者之间的协整关系不存在。具体步骤如下：

第二步：用ADF单根法检验残差序列et的平稳性。若et检验结果为0阶单整，即视为平稳的，则可判断yt和xt存在协整关系；若et的单整阶数大于等于1，则表示yt和xt之间不存在协整关系。

2 基于频率协整余量的损伤识别

2.1 损伤识别过程

通过求解多自由度体系动力特征方程，可将任意一阶振动频率表示为广义刚度K*和广义质量M*的形式

(1)

任意两阶频率fj和fi之间关系用式(2)表示

fj-γfi=0

(2)

当结构处于外界温度影响下，方程式(2)右端不再等于0。可推广为一般的表达形式

(3)

式中，αi,aj为协整系数；εt为外界温度影响的随机变量，在多样本情况下，其均值为零。

结构发生损伤时，两阶频率之间的协整关系将发生变化。若保持原有的协整系数不变，将损伤后的结构频率代入式(3)得

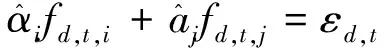
(4)

由式(4)减去式(3)，可得结构损伤前后的协整余量的变化量

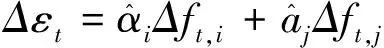
(5)

由此可知，损伤前后协整余量的变化值与温度无关，可剔除温度对频率的影响。结构发生损伤时，Δεt≠0，频率协整余量会发生阶跃现象。同时，为确保损伤识别的准确性，根据文献[8]结论，取训练样本协整余量标准差的3倍作为阈值，可包括95%以上的协整余量。当Δεt恒定超出±3σ时，即可判断损伤的发生。

2.2 抗噪性能分析

考虑噪声后，任意两阶频率的协整方程由式(3)转化为

(6)

整理方程得到

(7)

(8)

式中，Δδt,j和Δδt,i的数学期望值为0，Δεt在结构损伤前后会发生明显跳跃。可见，基于频率协整的结构损伤识别方法具有较好的抗噪性能。

3 自锚式悬索桥损伤识别分析

3.1 数值模型

以福州市首座独塔自锚式悬索桥——鼓山大桥主桥(跨径为150 m+235 m)为工程背景(如图1所示)。该工程建立了无线健康监测系统，系统布置了加速度传感器、连通管竖向位移传感器、水平位移传感器、温湿度传感器、倾角仪等。各传感均根据该桥易损性分析结果进行布置，确保数据的准确性和实用性。

图1 福州鼓山大桥Fig.1 Fuzhou Gushan Bridge

根据文献[9]研究结果，温度对悬索桥前6阶频率影响的最大值和平均值分别为1.975%和1.175%；实际桥梁上汽车荷载引起的频率变化最大值和平均值分别为0.262%和0.104%；而风荷载引起的频率相对变化的最大值和平均值分别为0.215%和0.163%。由此可见，交通荷载和风荷载对频率的影响相对温度的影响较小。鉴于此，仅考虑环境温度作用下的频率时间序列，验证本文提出方法的有效性。

由于实测信号没有损伤结构的数据，无法满足损伤识别验证需求。因此采用监测系统测得的温度记录数据(2016-01-01 ～2016-12-31)作为输入，进行不同工况的数值分析。温度值每隔4 h采集一次，共2 190个时刻的温度记录，变化范围从3～40℃，如图2所示。且将2016-01-01～2016-11-30期间采集的温度数据作为基准样本数据，计算得到共2 004个频率为结构完好状态下的样本；将2016-12-01～2016-12-31的温度数据作为计算结构损伤状态下的频率样本，共186个损伤样本。

图2 实测桥梁温度数据Fig.2 Authentic temperature data of bridge

3.2 频率时间序列的单根检验

自锚式悬索桥主梁和缆索的损伤对结构竖向振动频率的影响较大，选取主梁前4阶竖向振动频率作为分析对象。图3和图4绘制了鼓山大桥的前4阶振动频率随环境温度的变化曲线。从图中可看出，频率随温度变化呈现出非平稳状态，但要验证频率之间是否存在协整关系，必须满足1阶单整条件，可采用ADF方法进行检验。

为满足实际工程监测需要，采用式(9)模拟真实环境下的频率。

xinoise=xi+ε·R·std(xi)

(9)

其中，xinoise为考虑存在噪声的测量模态频率；xi是理论计算的频率；ε是噪声水平，本文取5%；R是服从(0,1)的正态分布随机数，即R～N(0,1)；std(xi)为xi的标准差。

表1列出考虑噪声影响后，前4阶竖向振动频率的单根检验结果，与不考虑噪声工况相比，噪声不影响频率时间序列单整性质，满足协整条件。

图3 环境温度下鼓山大桥第1阶和第2阶频率Fig.3 The first and second order frequencies of Gushan Bridge under ambient temperature

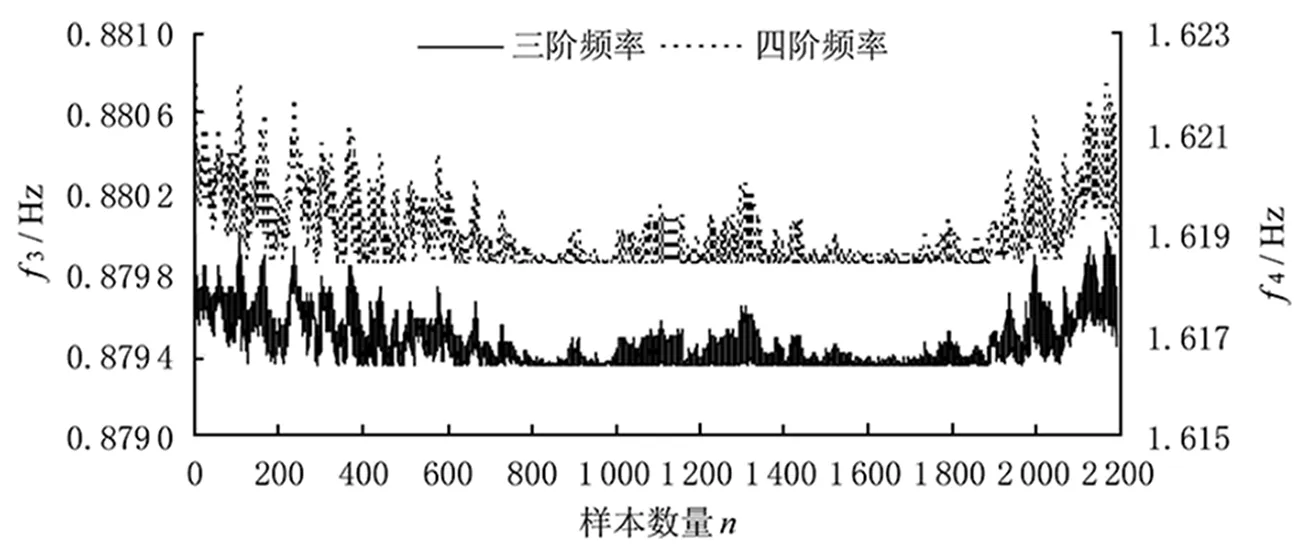
图4 环境温度下鼓山大桥第3阶和第4阶频率Fig.4 The third and fourth order frequencies of Gushan Bridge under ambient temperature

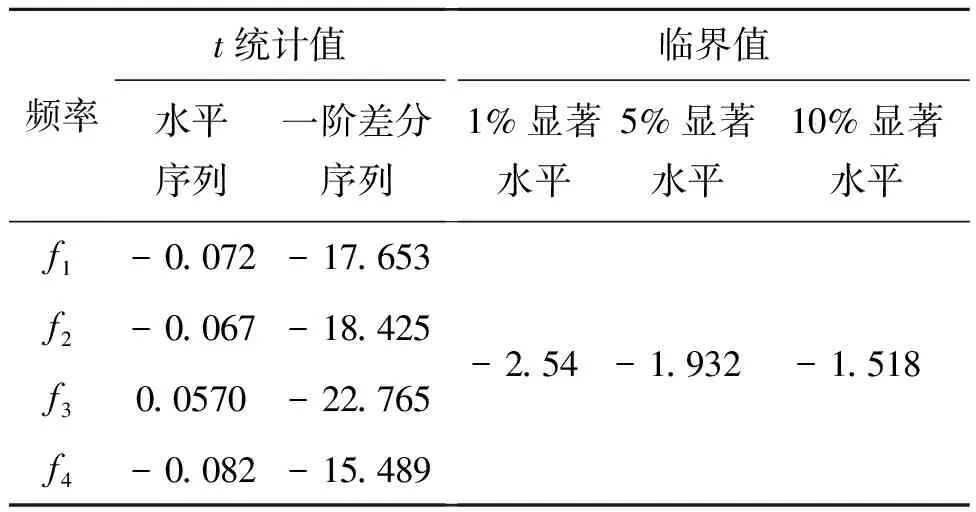
表1 主梁前4阶竖向频率单根检验

3.3 各阶频率之间协整关系的检验

图5和图6给出了考虑噪声后相应的残差时间曲线，从图中可初步判断各残差为零均值的平稳时间序列。

为确保残差序列为零均值的平稳序列，使用ADF方法对残差进行复检。从表2可知，在理论计算和添加噪声后模拟实际测量工况下，第1阶频率和第2阶频率之间的协整残差都平稳，第3阶频率和第4阶频率的协整残差也平稳。由此可见，各阶频率的时间序列存在协整关系，为进一步利用协整方法进行损伤识别打下基础。

图5 残差e1,2时间序列Fig.5 Time series of residual e1, 2

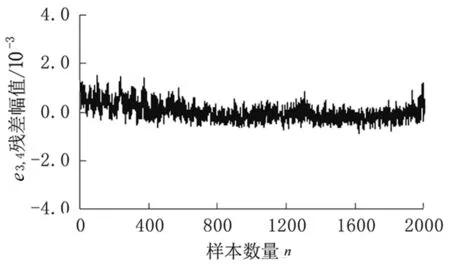
图6 残差e3,4时间序列Fig.6 Time series of residual e3, 4

表2 协整残差的单根检验

3.4 损伤识别结果分析

自锚式悬索桥的主塔刚度通常较大，局部的轻微损伤不会引起主梁竖向振动频率的变化。本文仅对主梁损伤、主缆损伤及吊索损伤进行识别。

结构损伤通常采用刚度折减来模拟，损伤单元的刚度为(EI)D=x(EI)，x为刚度折减系数，(1-x)为损伤程度。对主梁和主缆模拟了5%和10%的低损伤工况，对吊索则分析了10%和50%损伤工况。由于篇幅所限，且为验证本文提出方法的抗噪性能，文中仅给出了考虑噪声后的损伤识别结果。

(1)主梁损伤识别

根据易损性分析的结果，假设易损截面发生损伤，分别模拟了塔梁连接处截面、主跨跨中附近和短跨跨中附近截面的损伤。每个截面分别模拟了5%和10%的损伤程度。利用前4阶竖向振动频率的协整余量进行损伤识别，识别结果如图7所示，图中控制线为参考样本序列±3倍标准差。

从图7可看出，在环境温度影响下，基于频率协整的损伤识别方法能有效地识别主梁各截面位置的损伤，在5%低损伤的情况下，该方法同样有效。结构未发生损伤时，各协整余量大部分都在控制线以内，当结构发生损伤时，余量均值将发生突变。且损伤越大，突变越明显。f1-f2协整余量突变方向与f3-f4协整余量突变方向相反，且短跨发生损伤与主跨发生损伤相比，余量序列出现反向跳跃，这与各截面刚度对各阶频率的贡献有关。据此可通过余量突变方向初步判断出主梁损伤的大致区域。

图7 主梁损伤识别结果Fig.7 Damage identification results of the main beam

同时f1-f2协整余量对短跨的截面损伤较为敏感，塔梁截面位置次之，对主跨截面低损伤识别效果较差。f3-f4协整余量对塔梁截面位置损伤较为敏感，短跨截面位置次之，对主跨截面损伤敏感性较低。

与不考虑噪声的分析结果相比，考虑噪声后不改变各频率协整余量的突变性质，说明噪声对损伤区域的判断不会造成影响。利用主梁的前4阶竖向振动频率之间的协整关系，都能有效地识别损伤的发生，前2阶频率序列余量与后2阶频率序列余量之间形成互补关系，弥补了仅由两阶频率无法准确识别损伤的缺陷。

(2)主缆损伤识别

悬索桥的主缆损伤通常表现为截面腐蚀，整体抗拉刚度降低。文中分析了主缆损伤5%和10%两种情况，图8给出了f1-f2和f3-f4协整对法损伤识别结果。分析结果表明：主梁任意两阶竖向振动频率对主缆刚度变化较为敏感，考虑测量噪声影响后，f1-f2协整余量和f3-f4协整余量都能很好地识别出损伤，且f1-f2和f3-f4余量依然表现出相反的跳跃现象，其突变性质与短跨和塔梁位置损伤工况一致。

图8 主缆损伤识别结果Fig.8 Damage identification results of the main cable

(3)吊索损伤识别

以易损吊索S2(短跨第2根)和S33(主跨跨中附近)作为损伤识别的分析工况。由自锚式悬索桥的结构特点可知，吊索的轻微损伤对整体结构的影响较小，因此选择10%损伤和50%的损伤为分析工况，利用频率协整方法进行损伤识别。结果如图9和图10所示。

图9 吊索S2损伤识别结果Fig.9 Damage identification results of sling S2

图10 吊索S33损伤识别结果Fig.10 Damage identification results of sling S33

从图中可以看出，当吊索损伤10%时，频率协整余量序列对吊索损伤不敏感，主梁前4阶竖向振动频率的协整余量均被噪声淹没；当关键吊索损伤达到50%时，能有效识别出损伤。这说明，单根吊索的轻微损伤不足以引起主梁竖向刚度的变化，只有当损伤较大时才对主梁刚度有一定影响。从主梁频率角度识别吊索的损伤场景具有一定的局限性。

4 结论

1)从理论上分析了频率用于结构损伤识别的可能性，推导了基于频率协整的结构损伤识别算法，构建了协整余量损伤识别指标，同时考察算法的抗噪性能，说明提出方法的可行性。

2)将结构正常运营状态下采集的数据作为训练样本(训练样本应尽可能包括结构所处的各种环境)，计算得到训练样本的协整余量，再根据统计理论选取协整余量的控制线。以控制线为基准，在后期的监测过程中，若频率的协整余量超过了该控制线，表示结构有可能发生损伤；若在控制线以内，表示结构完好。

3)仅利用主梁前4阶竖向振动频率，能较好识别悬索桥主梁和主缆的损伤。且对不同位置的损伤，协整余量的突变性质也不同，可据此初步判断结构损伤区域。由于吊索损伤对主梁刚度影响较小，本文方法对吊索小损伤不敏感。