基于压电陶瓷应力波的套筒灌浆缺陷检测

(1.福建农林大学 交通与土木工程学院，福建 福州 350002；2.可持续与创新桥梁福建省高校工程研究中心，福建 福州 350108；3.福州市第三建筑工程公司，福建 福州 350011；4.福建工程学院 土木工程学院，福建 福州 350118)

随着城市化进程的加快，装配式建筑得到了行业的青睐[1]。目前，装配式建筑中的一部分构件之间主要通过套筒灌浆进行连接。然而，在实际工程中因加工精度、现场施工水平等原因，灌浆套筒极有可能出现漏浆、少灌的情况[2]。若套筒内部灌浆不饱满，受力钢筋的连接将有可能达不到预期性能，从而给结构带来安全隐患。因此，如何快速有效地检测灌浆套筒内部灌浆料的密实性非常重要。

近年来，研究人员通过首波声时法、X射线法、嵌入式传感器法等一些检测方法对灌浆套筒内部灌浆料的密实性进行检测。如聂东来等[3]根据超声波传播的路径不同来判断套筒灌浆料的密实性，但是这只是一种经验性方法，没有充分的理论依据[4-5]。陶里等[6]采用X射线对套筒灌浆的密实性进行检测，该方法虽然能够清晰直观地显示灌浆套筒缺陷的位置和尺寸，但X射线的放射性限制了其在施工现场的应用。Song等[7]通过嵌入式传感器法将开发的智能骨料(smart aggregate, SA)埋入套筒内部进行灌浆密实性的检测。但是，由于实际施工过程中有可能使用规格较小的套筒从而不便于将SA嵌入套筒内部。因此，研究一种经济、有效而且简便的套筒灌浆密实性检测新方法具有现实意义。

最近，压电陶瓷材料因其响应速度快、抗干扰能力强、经济等优点在结构健康监测中得到了广泛的应用。基于压电陶瓷材料的缺陷检测方法主要分为压电阻抗法[8]和应力波法[9]两大类，其中又以应力波法的应用最为广泛。如周天翔等[10]基于压电陶瓷应力波并通过构建损伤指标对钢筋混凝土-钢组合塔筒的开裂进行缺陷检测。Hong等[11]将压电陶瓷应力波法应用于内衬防腐管道分层破坏的损伤检测，验证了小波包分析和希尔伯特黄变换在管道分层损伤评估中的可行性。

虽然基于压电陶瓷应力波的损伤检测方法已经取得较多的研究成果，但在灌浆套筒密实性检测方面尚未见报道。基于此，本研究采用基于压电陶瓷应力波的灌浆套筒缺陷检测方法对一个灌浆套筒数值算例进行了分析。

1 基本理论

1.1 小波包分解理论

小波包变换既可以对低频信号进行分解，又可以对高频信号进行分解。因此，对包含大量中、高频信息的信号进行小波包变换能够得到更好的时频局部化分析结果[12]，其分解过程如图1所示。

(1)

经过j层的小波包分解后，原始信号f(t)可表示为

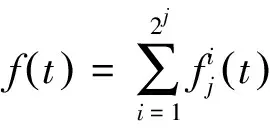
(2)

图1 小波包变换流程图Fig.1 Flowchart of wavelet packet transform

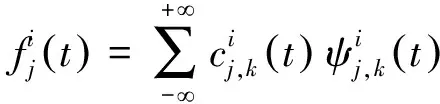
(3)

式中的小波包系数可表示为:

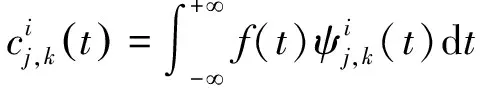
(4)

式中，小波包系数应满足正交条件：

(5)

由式(3)可知：通过小波包分解得到不同频带的小波包子信号，然后构建如式(6)所示的各子信号的小波包能量。

(6)

将式(3)代入式(6)，并利用正交条件式(5)，可得

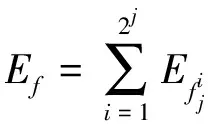
(7)

(8)

式中，Ef为信号f(t)的能量。

式(7)表示原始信号的总能量是由分解后不同频带内的小波包组分能量之和组成。由于小波包变换后的末层各子频带的能量对于信号特性的变化十分敏感，可用于表征信号的本质特征。

1.2 损伤指标的构建

在遇到套筒灌浆缺陷时，应力波能量的大小将会改变[13]，进而导致小波包分解后各子频带内的小波包能量发生变化，因此可根据缺陷状态和健康状态下小波包分解重构后各频带能量的变化来构建损伤指标，如式(9)所示。

(9)

式中，INX为所构建的套筒灌浆缺陷的损伤指标；EfH为健康状态下响应信号的小波包能量值；EfD为不同缺陷工况下响应信号的小波包能量值；D对应不同的灌浆套筒缺陷工况。由所定义的损伤指标可知：损伤指标越大，灌浆套筒缺陷也越大。

2 数值算例验证

2.1 灌浆套筒的缺陷设置

本研究的灌浆套筒缺陷的形状及其布置如图2所示。缺陷的大小根据其所在位置的弧长对应的弦长来表示。为研究灌浆缺陷的大小对激励信号的响应，考虑弦长和缺陷径向宽度两个参数，分别设置了10 mm×2 mm、20 mm×2 mm和30 mm×2 mm三种缺陷工况。其中，弦长长度记为L，分别取10、20、30 mm。缺陷径向宽度记为W，其值大小设为W= 2 mm。而健康工况下L和W均设置为0。

图2 灌浆套筒缺陷和压电陶瓷的布置Fig.2 Layout of sleeve grouting defects and piezoelectric ceramics

2.2 激励信号的选取

由于应力波在传播的过程中会出现频散效应，而降低频散效应的方法一般通过使用合适的窗函数来压缩频域带宽。因此，采用汉宁窗调制的周期为0.025 ms、中心频率f为40 kHz的正弦电压信号作为驱动器的激励信号，其表达式如式(10)所示。激励信号的幅值大小设为10 V，其时域图如图3所示。

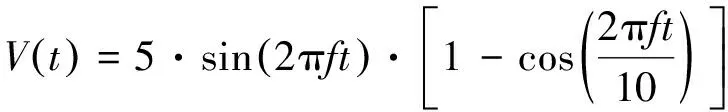
(10)

图3 激励信号时域图Fig.3 Time-domain diagram of the excitation signal

2.3 压电-机械耦合方程

压电方程根据边界条件的不同，可分为机械边界条件和电学边界条件，采用机械边界条件进行压电机械系统耦合，其压电方程为：

(11)

式中：S、E分别为应变张量和电场强度；T为应力张量；D为电位移；e为压电应力系数矩阵；et为e的矩阵转置；cE为弹性刚度系数；εS为恒定应变作用下的介电常数。

需要指出的是，在ABAQUS中定义压电陶瓷材料的性质时，首先要明确压电陶瓷的极化方向，并且要按照对应的极化方向来输入材料属性的各个矩阵。研究压电陶瓷所选用的极化方向为z轴，所需输入的参数分别为压电应力系数矩阵e、介电常数矩阵ε和弹性刚度矩阵C。

2.4 有限元模型的建立

首先通过三维实体单元来建立灌浆套筒模型，然后利用结构化网格划分技术进行各个部件的网格划分，最后通过隐式分析求解响应信号。采用的单元类型有多种，其中两端钢筋、套筒壁和灌浆采用系统默认的三维应力单元。由于结构化网格划分技术划分的六面体网格质量比扫掠网格划分技术划分的六面体及自由网格划分技术划分的四面体网格都要高，因此采用结构化网格划分技术对钢筋、套筒壁和灌浆进行六面体网格划分，其对应的单元类型为C3D8R(8节点六面体线性减缩积分单元)。考虑到压电陶瓷所具有的正逆压电效应，对于压电陶瓷片采用压电单元，其对应的单元有C3D8E、C3D6E和C3D4E 3种单元类型。为确保压电陶瓷片网格划分的质量，同样采用结构化网格划分技术划分为六面体网格，对应的单元类型为C3D8E。

考虑到模型的计算时间效率、精确性和响应信号的有效提取，需要对各个部件网格的大小、计算时间步长和计算总时长进行控制。若计算总时长过短，可能在传感器端提取不到所需的响应信号；若网格划分过大将使计算精度不够，而网格过小则计算效率偏低。因此，计算总时长和网格划分大小应满足以下要求：

(12)

(13)

式中：T为总时长；D为信号从压电陶瓷驱动器传播到压电陶瓷传感器之间的最短距离；v为波速；λmin为最小波的长度；m为最大单元的网格尺寸大小。

而对于计算时间增量步长Δt应同时满足式(14)和式(15)的要求。

(14)

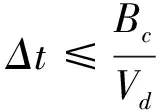
(15)

式中：Bc为网格的最小尺寸；Vd为应力波的传播速度；fmax为响应信号频率的最大值。根据上述要求，本文确定的两端钢筋网格大小为2.5 mm，灌浆的网格尺寸为3 mm，套筒壁网格尺寸为3.5 mm，模型单元网格如图4所示。模型计算总时长为0.3 ms，增量步Δt= 0.5 μs。

图4 模型网格的划分Fig.4 Meshing of the model

2.5 材料参数

研究使用的钢筋、灌浆、套筒及压电陶瓷的材料属性如表1所示。其中压电陶瓷的极化方向为z方向，压电陶瓷对应的压电应力系数矩阵e、介电常数矩阵ε、弹性刚度矩阵C分别如式(16)、(17)和(18)所示。

(16)

(17)

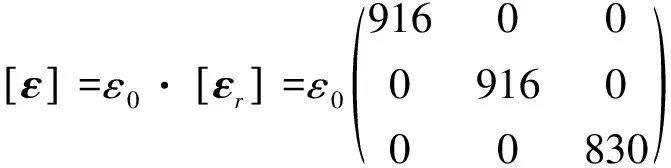
(18)

式中，真空中的介电常数ε0=8.84×10-12C/m。

表1 材料属性

2.6 响应信号的数据分析

首先采用有限元方法模拟各工况下灌浆套筒的响应信号，如图5所示。在对各种工况所对应的响应信号进行小波包变换前，首先需要选择合适的小波函数和分解层数以确保信号处理的效果。本文采用Daubechies(Db)小波函数系列，信号分解的层数及小波函数的阶数根据lp范数熵指标来确定[14-15]。经对比后发现：采用Db4小波函数且分解层数为3层的效果较好。

图5 各工况下灌浆套筒的响应信号Fig.5 Response signal of grouting sleeve under different cases

由图5可知，健康工况响应信号的波形幅值明显小于另外3种缺陷工况下对应的波形幅值，因此，可初步判断灌浆套筒是否密实。由于3种缺陷工况下对应的信号波形图相差甚小，为进一步精确判断灌浆套筒的密实程度，将对各工况下的响应信号进行小波包变换并提取信号的特征参数，以进一步获取特征参数与灌浆套筒密实程度之间的关系。

由文献[16]可知：根据响应信号经小波包分解后某个或某几个子频带能量的变化可以有效识别结构的损伤情况，并且能够凸显损伤检测效果。因此，以弦长为30 mm缺陷工况下的响应信号为例，其对应的应力云图如图6所示。按照选用的小波函数和分解层数，直接通过MATLAB程序工具箱对响应信号进行小波包变换，得到如图7所示的第3层各频带的波形图。

图6 30 mm灌浆缺陷工况下的应力云图Fig.6 Stress nephogram of the condition with a 30 mm grouting defect

由于响应信号的采样频率为2 MHz，由采样定理可知奈奎斯特采样频率为1 MHz。而响应信号经3层小波包分解后可得23=8个子频带，因此每个频带的带宽为1 MHz/8= 125 kHz，据此求得第1频带的频率区间为0～125 kHz。由于激励信号的中心频率为40 kHz，因此信号的能量将主要分布在第1频带内。从图7可以看出：第3层第1频带重构后的波形图与原始响应信号波形图非常接近，并且经计算得其能量值占原始响应信号能量的99.97%。上述结果表明：本文选用Db小波函数对响应信号进行3层小波包分解是十分合理的。

同弦长30 mm缺陷工况一样，将其余缺陷工况与健康工况下的响应信号进行3层小波包变换，计算出各工况下对应的第3层各频带小波包能量值，结果如表2所示。

图7 小波包重构后第3层各频带波形图Fig.7 Waveforms of each band in the third layer after wavelet packet reconstruction

工况第1频带第2频带第3频带第4频带第5频带第6频带第7频带第8频带健康2.69E-061.60E-099.87E-123.68E-123.90E-141.92E-152.18E-151.16E-1410 mm缺陷2.45E-051.10E-085.55E-118.43E-122.10E-139.71E-162.58E-158.94E-1520 mm缺陷2.90E-051.09E-089.96E-112.14E-102.37E-134.59E-142.35E-131.27E-1230 mm缺陷3.72E-051.25E-086.58E-114.80E-112.53E-131.17E-116.61E-143.64E-13

由表2可知：响应信号经3层小波包分解重构后，小波包能量绝大部分集中在第3层的第一频带内，而且第3层第一频带的小波包能量值随着灌浆缺陷弦长的增加而不断增大。

在此基础上，采用所构建的损伤指标INX来直观表示灌浆套筒缺陷与各工况下小波包总能量之间的关系，结果如表3所示。

表3 各工况对应的指标值

由表3可知：各工况下的损伤指标值INX随着灌浆套筒缺陷弦长的增加而增大，其中，健康工况下的损伤指标值INX最小。出现这种现象的原因是：套筒内部的灌浆缺陷导致应力波的传播路径发生变化。当灌浆密实时其传播路径为径向传播；而当内部存在灌浆缺陷时，应力波将先沿套筒壁传播，之后再透射灌浆料传播，从而减少了应力波在灌浆料中传播的路径。而且由于应力波在灌浆介质中传播的阻尼较在套筒壁钢材介质中传播的阻尼大，激励信号产生的应力波在套筒壁中传播的成分将随着缺陷弦长的增加而增大，进而导致应力波在传播路径中衰减的能量减少[13]。由以上数值算例结果可知：所提出的小波包能量损伤指标INX能够有效识别灌浆套筒的密实及密实程度，不失为一种行之有效的损伤指标。

3 结论

1) 在所选用的汉宁窗调制的中心频率为40kHz的正弦电压激励信号作用下，对所得响应信号进行3层小波包分解重构后，第3层频带中第一频带所占的能量比例较大，这表明所选取的激励信号、小波函数及分解层数是可靠的。

2) 各工况下的响应信号经小波包变换后其小波包能量主要集中在第3层的第1频带内，且由各工况下的小波包能量值可知：随着套筒灌浆缺陷弦长的增加，第1频带的能量值也随之增大。

3) 由于损伤指标INX随着灌浆缺陷弦长的增加而增大，它较好地表征了套筒内部灌浆料的缺陷程度。