水平受荷桩在桩顶嵌固时的刚度系数新解法

陈国周，林智勇，林文彬

(1.福建工程学院 土木工程学院，福建 福州350118；2.闽台合作土木工程技术福建省高校工程研究中心，福建 福州350118)

水平受荷桩又称为抗水平力桩，在桥梁、港口码头、滑坡治理、高层建筑等工程中被广泛应用。桩受到水平荷载作用时，桩土之间的互相作用较复杂，桩的内力及变形计算一直是一个重要的研究课题。水平受荷桩的理论模型和计算方法很多，根据地基水平抗力的不同假定有张氏法、m 法、k 法、c 法，考虑土体抗力与桩的变形关系的p-y曲线法等[1]。由于m法在桩基小变形时计算结果与实际工程较为吻合，在工程界得到广泛应用，被列入我国多部规范，如铁路桥涵地基和基础设计规范[2]、公路桥涵地基和基础设计规范[3]和建筑桩基技术规范[4]等。

许多学者在m法应用方面进行了深入的研究。赵明华[5]采用幕级数求解，研究推导出一整套适合于我国工程应用的倾斜荷载受力桩的m法设计理论和计算方法。杨美良等[6]考虑桩基的剪切变形影响，用单广义位移深梁理论，建立了桩基m法的计算方法，导出了初参数表达式和无量纲参数函数的统一表达式。李洪江等[7]推导考虑侧壁摩擦力的桩基水平承载挠曲微分方程，提出小变形下考虑摩擦效应的桩基水平承载计算方法。李微哲等[8]引入初始地基比例系数，提出了基于m法的双曲线型p-y曲线。毛坚强等[9]采用m 法模型模拟桩前滑体对桩的抗力，并分别对桩在滑面以上、以下的部分建立计算方程，应用幂级数法解得其位移及内力的表达式，最终得到整个桩的变形和内力以及桩、土之间的作用力。Xenia等[10]研究了水平受荷桩的水平刚度系数，提出一种新的弹性动力分析模型。António等[11]分析了足尺桩基模型试验的数据，归纳出水平受荷桩的变形及弯矩分布规律。

目前，水平受荷桩的刚度系数改进方面的研究还比较少。本文针对水平受荷桩刚度系数的传统计算公式复杂、计算量大的缺点，使用桩顶嵌固的边界条件推导出水平受荷桩刚度系数新的表达式并分析桩径及土体m值对刚度系数的影响。

1 水平受荷桩刚度系数的传统计算方法

1.1 桩身变形的微分方程

水平受荷桩示意图如图1.

图1 水平受荷桩示意图Fig.1 Sketch of pile under horizontal load

根据材料力学微块平衡及土层抗力沿深度线性变化的假定，可推导出如图1所示的桩身变形的微分方程如下

(1)

(2)

式中：a为桩的变形系数或称桩的特征值；yz为桩的水平变形值；z为计算点到桩顶的距离；m为土层水平抗力系数沿深度的比例系数；b0为桩的计算宽度；EI为桩的抗弯刚度。

1.2 微分方程的幂级数解

式(1)可用幂级数展开来求解，只要知道桩顶的水平位移y0、转角φ0、弯矩M0及剪力Q0,便可求得桩身任截面的水平位移yz、转角φz、弯矩Mz及剪力Qz的计算公式：

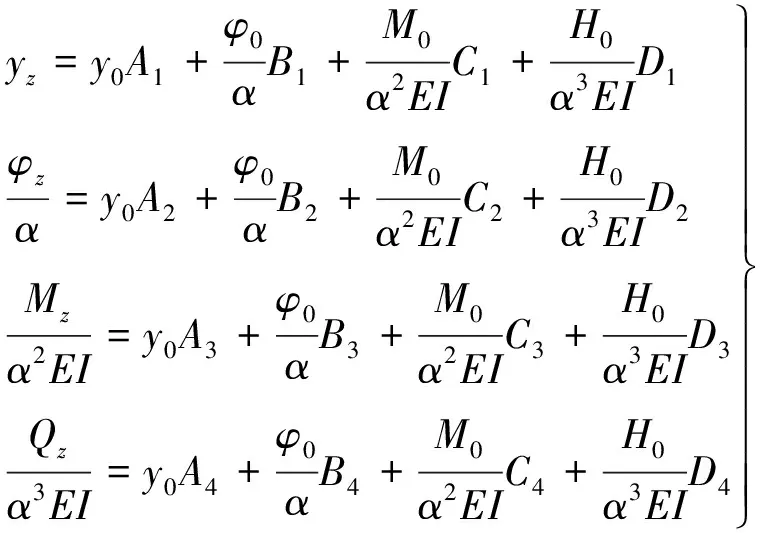
(3)

式中A1、B1、…、C4、D4为无量纲系数，而A2、B2、C2、D2是A1、B1、C1、D1的一阶导数，A3、B3、C3、D3是A1、B1、C1、D1的二阶导数，A4、B4、C4、D4是A1、B1、C1、D1的三阶导数。A1、B1、C1、D1表达式如下

(4)

(5k-4)!!=

(5k-4)[5(k-1)-4]…(5×1-4)

(5)

(5k)!=(5k)(5k-1)…2×1

(6)

1.3 柔度系数

要求解式(3)，需要桩顶的水平位移y0、转角φ0、弯矩M0及剪力Q0。引入柔度系数，该系数表示受到单位荷载而产生的相应位移。假设桩底自由，则可推导出柔度系数表达式如下

(7)

(8)

δHM=δMH

(9)

(10)

式中δij表示j方向受到单位荷载时在i方向产生的相应位移。当i=H时，表示水平位移；当i=M时，表示转角。当j=H时，表示水平荷载；当j=M时，表示弯矩。

桩顶的水平位移y0、转角φ0可以用柔度系数表示为

φ0=-H0δMH+M0δMM

(11)

y0=H0δHH+M0δHM

(12)

本研究在推导过程中假定了桩底是自由的，如果桩端土的约束不可忽略，则在柔度系数表达式中需要增加这部分的影响。

1.4 刚度系数

刚度系数表示单位位移而产生的相应内力，本研究推导桩顶嵌固时的刚度系数，如图2所示，桩顶嵌固时，在桩顶的转角为0。

图2 桩顶嵌固示意图Fig.2 Sketch of pile with its top embedded

把φ0=0代入式(11)，得

(13)

把式(13)代入式(12)，得

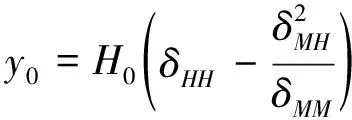
(14)

令y0=1(即单位水平位移)

得

(15)

(16)

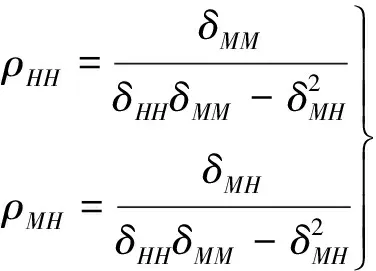
(17)

式中ρHH为水平刚度系数，ρMH为转动刚度系数。

把式(7)-(10)代入式(17)，得

(18)

式(18)是现行规范所用的计算式。

2 刚度系数新解法

2.1 推导过程

桩顶嵌固，产生单位水平位移，则边界条件为φ0=0，y0=1。桩底自由，则有边界条件为Mh=0，Qh=0。把这两个边界条件代入式(3)，得

(19)

只需取后面两个式子

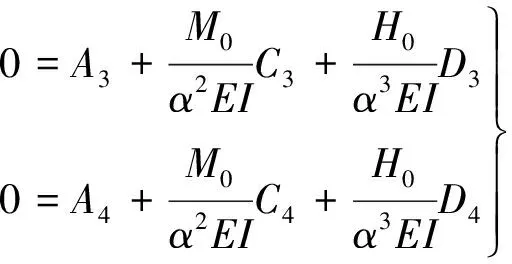
(20)

得

(21)

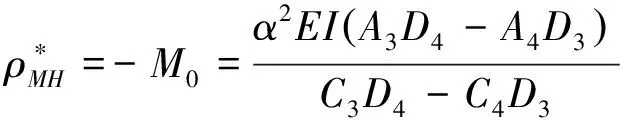
(22)

2.2 新解法的证明

把A1、B1、C1、D1求二次导数得到A3、B3、C3、D3。根据级数展开，得

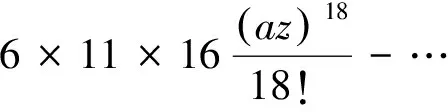
(23)

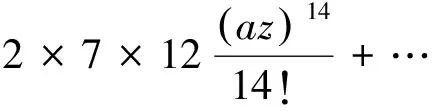
(24)

(25)

(26)

把A1、B1、C1、D1求三次导数得到A4、B4、C4、D4根据级数展开，得

(27)

(28)

(29)

(30)

根据式(23)至式(30)，可得

B4C3-B3C4+A3D4-A4D3=0

(31)

上式两边乘以A3D4-A4D3

(B4C3-B3C4)(A3D4-A4D3)+

(A3D4-A4D3)2=0

(32)

把上式展开，并移项

A3B4C3D4+A4B3C4D3=

A3B3C4D4+A4B4C3D4-(A3D4-A4D3)2

(33)

上式两边减去(A3B4C4D3+A4B3C3D4)，得

A3B4C3D4-A3B4C4D3-A4B3C3D4+A4B3C4D3=

A3B3C4D4-A3B4C4D3-A4B3C3D4+A4B4C3D4-

(A3D4-A4D3)2

(34)

合并同类项，得

(C3D4-C4D3)(A3B4-A4B3)=

(B3D4-B4D3)(A3C4-A4C3)-(A3D4-A4D3)2

(35)

两边乘以(α2EI(A3D4-A4D3))，并移项，得

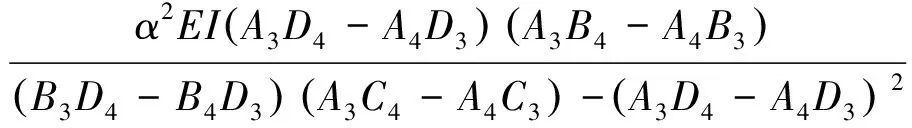
(36)

即

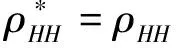
(37)

同样方法，可以证明

(38)

证毕。

3 算例

3.1 算例参数

某单桩与承台连接，假定桩顶为嵌固。桩截面直径d= 1.0 m，h= 10 m，桩身混凝土C30，保护层厚度取0.05 m，配筋率ρg= 0.004，水平抗力系数的比例系数m=2×104kN/m4，钢筋弹模Es=2.1×108kN/m4，混凝土弹模Ec=3×107kN/m4，计算该水平受荷桩的刚度系数。根据建筑桩基技术规范，计算桩顶嵌固时的刚度系数。

扣除保护层后的有效直径

d0=0.9 m

桩身截面抵抗矩

桩截面惯性矩

桩身抗弯刚度

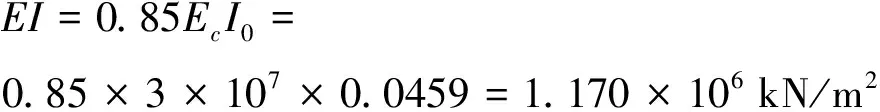
b0=0.9×(1.5×1+0.5)=1.8 m

桩的水平变形系数

3.2 传统方法计算刚度系数

采用建筑桩基规范方法计算

1.684 0×10-5m/kN

5.575 3×10-6kN-1

3.001 4×10-6(kN·m)-1

1.542×105kN/m

2.865×105kN·m/m

3.3 采用本文提出的新解法

0.498 53×1.17×106×

1.542×105kN/m

0.498 52×1.17×106×

2.865×105kN·m/m

比较计算结果可知

3.4 影响因素分析

3.4.1 桩径影响

实际工程中，桩截面直径和土体m值变化范围较大，对刚度系数计算结果影响较大，因此对这两个因素进行分析。采用本算例的参数，分别计算出桩截面直径d为0.8、0.9、1.0、1.1、1.2、1.3 m所对应的刚度系数。

如图3所示，桩径对刚度系数影响较大，其中水平刚度系数大约按桩径的两次方进行增长，转动刚度系数大约按桩径的三次方进行增长。

图3 桩径对刚度系数的影响Fig.3 Impact of pile diameter on stiffness coefficient

图4 土体m值对刚度系数的影响Fig.4 Impact of the m value of soil on stiffness coefficient

3.4.2 土体m值影响

根据本算例的参数，分别计算出土体m值为4×103、8×103、12×103、16×103、20×103、24×103kN/m4所对应的刚度系数。如图4所示，土体m值对刚度系数也有一定的影响，其中水平刚度系数大约按m值的0.6次幂进行增长，转动刚度系数大约按m值的0.4次幂进行增长。

4 结论

1)用本文提出的解法计算桩顶嵌固时的刚度系数与传统方法在计算结果上是一样的，而新解法减少了大量的计算量。

2)桩径对刚度系数影响较大，其中水平刚度系数大约按桩径的两次方进行增长，转动刚度系数大约按桩径的三次方进行增长。

3)土体m值对刚度系数也有明显的影响，水平刚度系数大约按m值的0.6次幂进行增长，转动刚度系数大约按m值的0.4次幂进行增长。

4)新解法假定桩顶嵌固，适用于桩顶与承台刚性连接的情况。在推导过程中假定了桩底是自由的，如果桩端土的约束不可忽略，则在刚度系数表达式中需要增加这部分约束的影响，这需要后续的进一步研究。