多胞不确定时滞系统的输出反馈鲁棒预测控制

盖俊峰，赵国荣，高 超，耿宝亮

（1.91206部队，山东青岛266108；2.海军航空大学，山东烟台264001）

随着模型预测控制理论的日趋成熟，对于不确定对象的鲁棒模型预测控制的研究成为当前预测控制领域的热点问题。鲁棒预测控制的实质是在线求解一个关于系统未来状态和输入的min-max 优化问题[1]。对于多胞模型描述的不确定系统，线性矩阵不等式（Linear Matrix Inequalities，LMI）成为鲁棒预测控制器设计的重要工具。1996年，Kothare等[2]率先提出了针对多胞不确定系统的鲁棒预测控制器设计方法。该方法将鲁棒预测控制问题转化为由LMI 描述的优化问题，为后来采用LMI方法设计鲁棒预测控制器及处理约束条件的研究奠定了理论基础。文献[3]用LMI方法设计了一种高效鲁棒预测控制器，在性能分析的基础上，提出了改善鲁棒预测控制次优性的方法。

近年来，针对不确定时滞系统鲁棒预测控制的研究也取得了若干成果[4-17]。其中，文献[5]针对一类多胞模型描述的不确定时滞系统，提出了一种带有时滞补偿的时滞相关鲁棒模型预测控制方法。将难以求解的min-max 优化问题转化为带有LMI 约束的凸优化问题，设计了能保证闭环系统稳定的鲁棒模型预测控制器，并证明了其控制算法的可行性。目前所见的研究成果中，控制器设计方案大多采用状态反馈，这要求系统的状态始终是可测的。但在实际工业生产及工程控制领域，系统的状态往往是不能直接测量得到的。对于时滞系统，采用状态反馈设计控制器时往往只考虑当前的状态信息，却忽略了时滞对系统的影响，因而使设计出的控制器具有较高的保守性。

鉴于上述状态反馈预测控制器的局限性，本文针对一类具有多胞结构的不确定离散时滞系统，提出了一种基于LMI 的输出反馈鲁棒预测控制算法。根据Lyapunov稳定性理论，给出了保证系统鲁棒稳定性的充要条件，并将系统的预测控制优化问题转化为易于求解的LMI 问题。在设计输出反馈预测控制器的过程中，为了减少在线计算量，对输出反馈增益矩阵的计算是离线实现的。对系统输入、输出约束和状态时滞的考虑使所提出的鲁棒预测控制算法更接近于工程实践。仿真结果验证了本文所提出方法的有效性。

1 问题描述

被控对象系统选为如下具有多胞结构的不确定离散时滞系统：

式（1）中：x( k )∈ℝn、u( k )∈ℝm和y( k )∈ℝl分别为系统的状态、控制输入和输出；U ⊆ℝm和Y ⊆ℝl分别为系统的输入约束集和输出约束集；矩阵C 为适当维数的常数矩阵；τ ＞0 为时滞常数；φ( k )为初始向量；矩阵A( k)、Aτ( k)、B( k )共同表征了系统模型中的参数不确定性，且都属于凸集Ω ，而Ω 为具有N 个顶点Ω1,Ω2,…,ΩN的凸多面体。

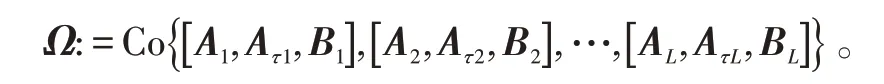
式中：Co 表示多面体的凸壳；[ Aj,Aτj,Bj] 则为凸壳的顶 点。 即 存 在 L 个 非 负 系 数 0 ≤λj( k )≤1 ，j=1,2,…,L，使：

式中：Ny为预测域；Nu为控制域，且Nu≤Ny；Q、R为给定的加权矩阵。

为了使系统输出能对设定参考轨迹进行有效跟踪，给出如下的误差积分器：

式中：yr(k)为期望参考轨迹；e(k)=Cx(k)-yr(k)为系统输出跟踪误差。

将积分器（2）加入到系统模型（1）后，简便起见，可将模型重写为：

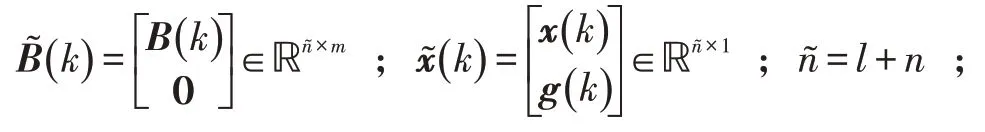
2 输出反馈预测控制器设计

现有文献多见采用状态反馈的控制器设计方案，但在实际工业生产及工程控制领域，系统的状态往往是不能被直接测量到的，而系统输出一般可直接测量。对于时滞系统，采用状态反馈设计控制器往往只利用当前的状态信息，却忽略了时滞对系统的影响，因而使设计出的控制器具有较高的保守性。鉴于上述状态反馈预测控制器的局限性，本节给出的控制器设计方案采用输出反馈。因而具有一定的工程应用价值。

针对系统重构模型（3），设计输出反馈模型预测控制器的形式如下：

在k 时刻预测的k+d 时刻的输入、输出和期望参考轨迹的预测值分别定义为u( k+d )，y( k+d )和yr( k+d )∈ℝl，其中d ≥1。预测域为Ny，控制域为Nu，且Nu≤Ny。当i={Nu,Nu+1,…,Ny-1} 时，有ϕij=O。

系统（3）在k+d 时刻的预测状态为

式中，d={0 ,1,…,Ny-1} 。

定义包含未来预测状态和期望参考轨迹为：

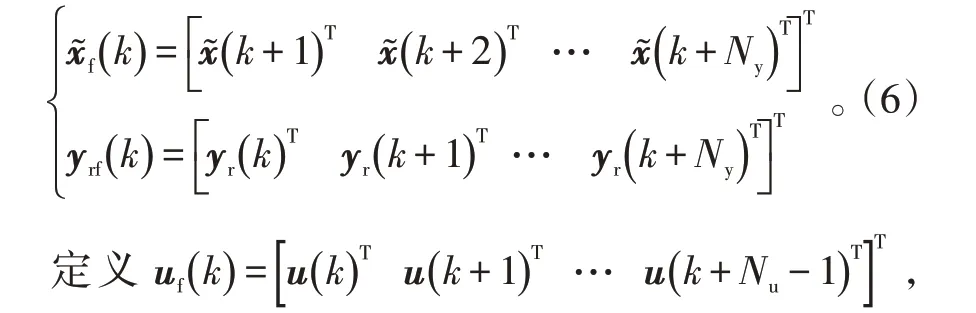
对式（5）进行处理，可得系统状态的模型预测值为：

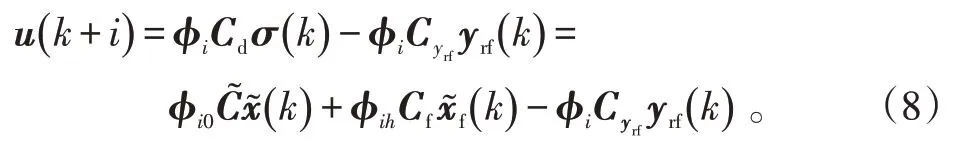
或者表示为如下简略形式：

式（9）中：

模型（7）在无限最优域上的代价函数形式如下：

式中，

式（11）中：Qd∈ℝn͂×n͂、Rd∈ℝm×m分别是半正定和正定矩阵。

对 所 有 的 d ， 有 Q=diag(Q0,Qf)，Qf=diag{Q1,Q2,…,QNy} ，R=diag{R0,R1,…,RNu-1} 且Qi=qiI ， Rj=hjI ， qi,hj＞0 ， i={0 ,1,…,Ny} ，j={0 ,1,…,Nu-1} 。

3 稳定性分析

在上节中，已经构造了系统状态预测模型（7）。将式（7）中的uf( k )用式（9）代替，可得闭环模型预测式如下：

式（12）中，

由于向量yrf( k )与状态向量x͂( k )相互独立，那么闭环系统（12）的稳定性和鲁棒性将不受yrf( k )的影响。因此，根据Lyapunov 稳定性原理，在分析系统鲁棒稳定性或者设计鲁棒控制器时，将向量yrf( k )设定成零向量并不失一般性。故闭环模型预测式（12）可以表示如下：

式（14）中：

本文研究的目标是在给定预测域Ny和控制域Nu的前提下，为对象系统设计一个带有输出反馈（9）的鲁棒模型预测控制器，且能保证闭环系统（14）的稳定性。

3.1 Lyapunov函数的选定

针对闭环系统（14），选取如下的Lyapunov函数

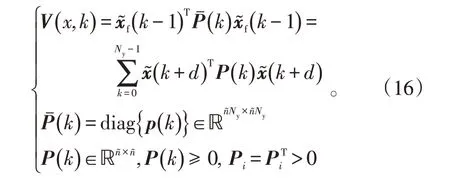
函数V( x,k )的一阶差分方程ΔV( x,k )可表示为：

由式（14）可得：

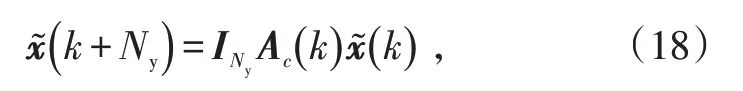
式中，INy=[O … O I ]∈ℝn͂×n͂Ny。

由Lyapunov 稳定性理论可知，当式（17）为负，即所选取的Lyapunov函数V( x,k )递减时，闭环系统为渐近稳定的。因此，可通过函数V( x,k )的一阶差分方程ΔV( x,k )的符号来判定系统的渐近稳定性。

3.2 基于LMI的鲁棒稳定性条件

在本节中，为第2 节中设计的鲁棒输出反馈预测控制器给出了保证系统鲁棒稳定性的一个充要条件，并将系统的预测控制优化问题转化为LMI 问题。为了将控制过程中的二次矩阵不等式转化为便于处理的LMI，通常会用到如下的Schur补引理。

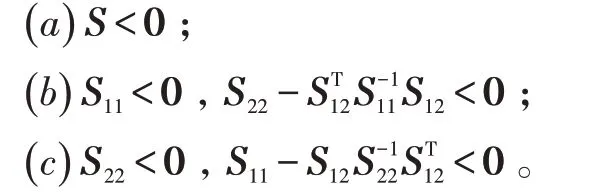
证明：( a )⇔( b )，由于S 为对称阵，故有S11=，S22=，S21=。应用矩阵的块运算规则可得。

故有

( a )⇔( c )，由于

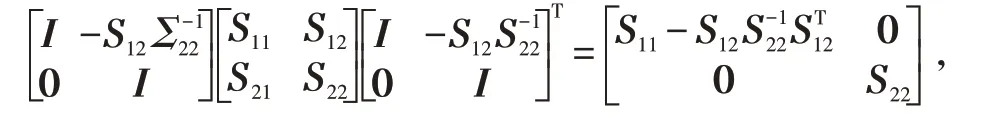
故有

定理1得证。

为第2节中设计的鲁棒输出反馈预测控制器所给出的保证系统鲁棒稳定性的充要条件，总结为如下定理。

定理2：具有Lyapunov 函数（16）的闭环系统（14）是鲁棒稳定的，当且仅当存在矩阵K ∈ℝn͂Ny×n͂()Ny+1和矩阵Φ，使如下的LMI成立。

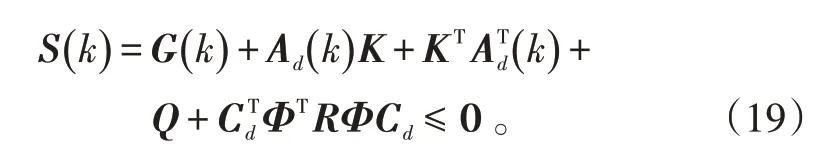
式（19）中：

证明：充分性：不失一般性，令Qk=O，Rk=O。

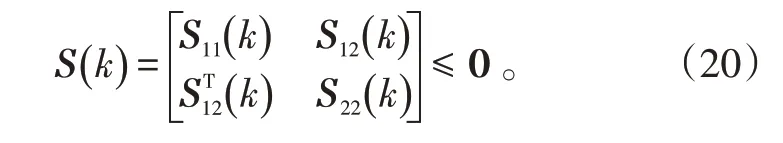
式（20）中：

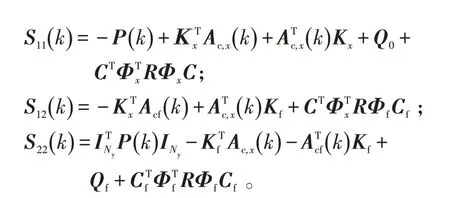
对式（20）进行整理可得

则有

由式（17）、（22）得：

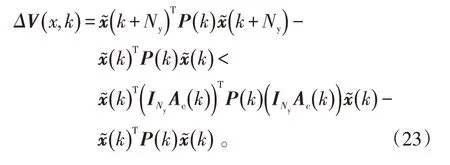
由式（22）、（23）可得：

即Lyapunov函数（16）单调递减，则闭环系统是鲁棒稳定的。

充分性得证。

必要性：假设存在对称正定矩阵P( k )使鲁棒稳定性条件（17）成立；必要的，存在一个标量ε ＞0，使得：

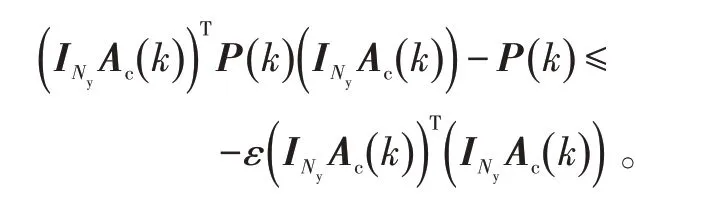
上述不等式可以被重写为：

对式（25）应用Schur补引理可得：

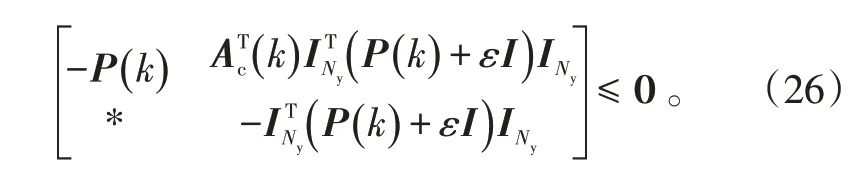
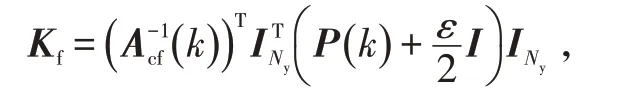
经过处理后得到：

式（27）中：

当ε →0 时，不等式（20）和不等式（19）可分别得到，必要性得证。

由式（19）可得如下的多胞系统LMI：

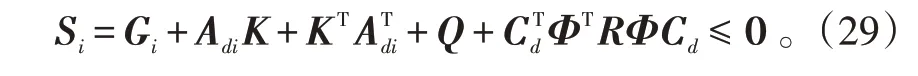
式（29）中：i={1 ,2,…,N }；Adi=[ Acxi-Acfi]T；Gi=diag{- Pi,PiINy} =diag{- Pi,O,…,O,Pi} 。

若式（29）在未知对称阵Pi=＞O,i={1 ,2,…,N}和矩阵K 下成立，且有可行解，则反馈增益矩阵Φ 在定义的凸集Ω 内保证了闭环系统的鲁棒稳定性。

4 基于LMI的鲁棒模型预测控制算法

为减少在线计算量，本文的预测控制算法对输出反馈增益矩阵Φ 的计算是离线实现的。根据模型预测控制的滚动优化策略，仅有矩阵Φ 的第1个元素ϕ0用来计算施加于控制对象的控制作用u( k )，Φ 的其他元素用来预测系统的未来状态或输出。而式（4）则实现了实际控制作用u( k )的在线计算。

由式（9），可得到实际控制作用如下：

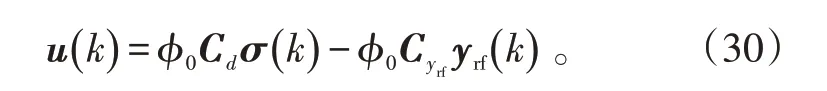
式中，Cd、Cyrf和σ( k )在第2节中已经作了定义。

式（31）中：Ac=Acf( k)-1Ac,x( k )；Aτ=Acf( k)-1Axτ( k )；Bc=-( k )Bcf( k )。

得到向量σ( k )的形式为：

将式（30）中的σ( k )用式（32）代替，得到实际控制作用u( k )的在线计算结果为：

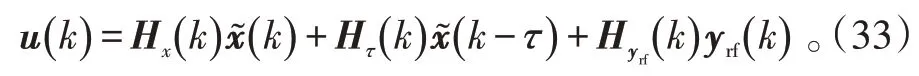
式（33）中，

综上所述，当x( 0 )=x0时，本文基于LMI 的输出反馈鲁棒模型预测控制算法可总结如下：

Step 1：令k=1。设置控制时间终点为T ，预测域为Ny，控制域为Nu；

Step 2：对式（29）求解；

Step 3：利用Step 2得到的解离线计算输出反馈增益矩阵Φ；

Step 4：通过被控对象获得新的当前输出值，并用系统模型预测输出值；

Step 5：计算u( k+i )，i=0,1,…,Nu-1，从而可得到最优控制序列uf( k )；

Step 6：将uf( k )应用于模型预测，仅将uf( k )的第1项u( k )作用于系统；

Step 7：如果k ＜T ，令k：=k+1，返回Step 4；否则结束。

5 仿真分析

考虑如下的多胞不确定离散时滞系统：

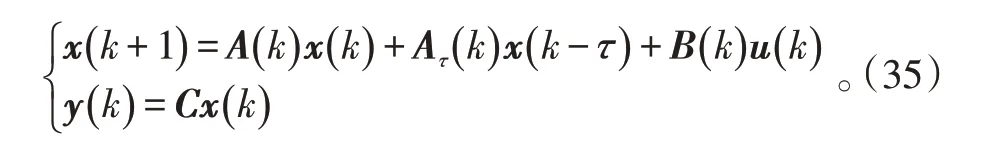
式（35）中：

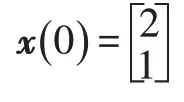
基于LMI的鲁棒预测控制问题较易求解，因其求解过程不需要进行任何参数调整，可一次性求解多个变量。利用上述数据，通过LMI Toolbox 对式（29）求解，可得输出反馈增益矩阵Φ 及矩阵Hx( k )、Hτ( k )、Hyrf( k )的值，由第4 节中的鲁棒预测控制算法得出使控制性能指标最小且使闭环系统渐近稳定的最优控制序列。本例中的参考轨迹设定为一方波信号。仿真结果如图1～3 所示。其中，图1 为系统输出对参考轨迹的跟踪曲线，y1、y2分别为2 个不同顶点的系统输出，yr为参考轨迹；图2为控制输入曲线u1、u2分别为2 个不同顶点的控制输入；图3 为鲁棒控制性能指标变化曲线。图1 表明，误差积分器的加入使系统输出能有效跟踪参考轨迹，且能满足输出约束条件；图2表明，控制输入能满足输入约束条件；图3 表明，鲁棒预测控制性能指标在滚动时域内实现了在线最小化。

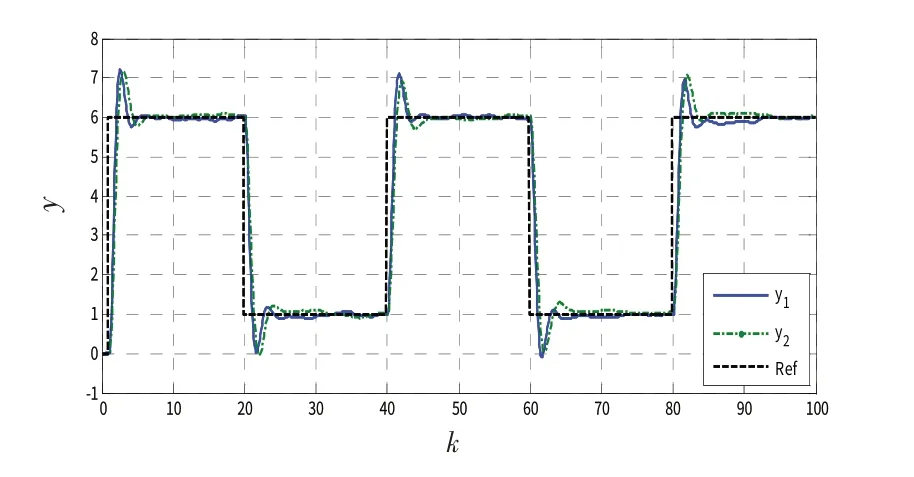
图1 系统输出跟踪曲线Fig.1 System output tracking curve

图2 控制输入曲线Fig.2 Control input curve

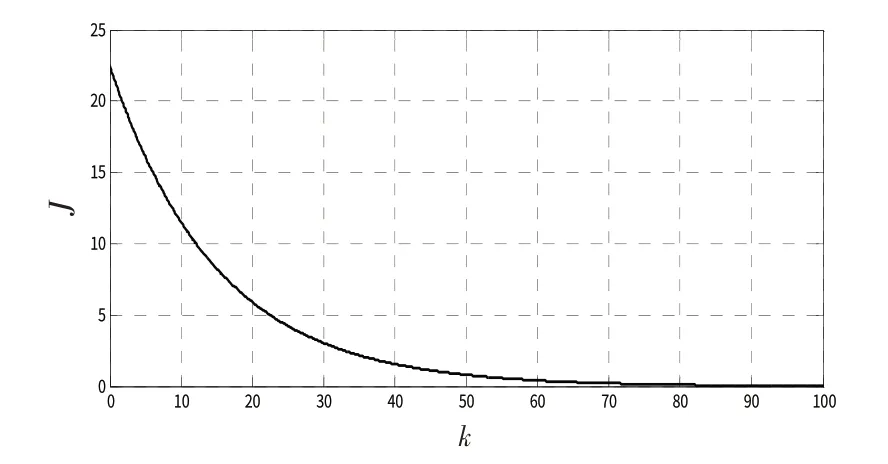
图3 性能指标变化曲线Fig.3 Performance indicator change curve

6 结论

本文针对一类具有多胞结构的不确定离散时滞系统，提出了一种基于LMI的输出反馈鲁棒预测控制算法。根据Lyapunov稳定性理论，给出了保证系统鲁棒稳定性的一个充要条件，并将系统的鲁棒预测控制优化问题转化为易于求解的LMI 问题。通过离线计算鲁棒预测控制器中的输出反馈增益矩阵，大大减少了算法的在线计算量。对系统输入、输出约束和状态时滞的考虑，使所提出的鲁棒预测控制算法更接近于工程实践。而输出反馈的采用突破了以往算法中要求系统状态必须可测的限制，使算法具有更低的保守性。实际工业过程中的系统输出一般是直接可测的，因而本文的输出反馈鲁棒预测控制算法具有一定的工程应用价值。