全地形移动机器人悬架减振机构动力学研究
黄玉成,许德章
(安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
随着人们对未知世界的不断探索,人类所使用的移动载体不断变化。人们在探查危险复杂的环境时,全地形移动机器人发挥着至关重要的作用,协助探测并保障探险过程中人类生命安全[1-2]。全地形移动机器人在小区户外巡检、农场农作物检测以及户外运输方面同样发挥着重要作用,让人类从复杂危险的劳动环境中解放出来,提高了生产效率并降低了劳动成本。全地形移动机器人的可靠运行是保障以上工作能够顺利完成的重要前提,而车身运动稳定性是其可靠运行的重要前提[3],因此对改善机器人车身运动稳定性的研究具有重要意义。改善机器人运行颠簸程度的方法数不胜数,如通过预先编制智能算法来控制车身运动姿态,从而改善车身振动程度[4];通过设计出不同类型的行走部件,改善行走部件与地面的贴合度,进而改善车身振动状态[5]。实验主要研究移动机器人的悬架减振机构,利用悬架减振机构来改善移动机器人车身振动。通过对独立悬架减振机构进行动态分析,确定影响悬架减振机构减振效果主要参数,并通过仿真实验分析,确定悬架减振机构的减振器参数取值范围,完成全地形移动机器人悬架减振机构的参数设置,使机器人具有良好的减振效果。
1 独立悬架减振机构动力学分析
1.1 全地形移动机器人结构介绍
针对全地形移动机器人独立悬架减振机构进行动力学分析,确定影响悬架减振机构减振效果的主要因素,所研究的全地形移动机器人的三维结构图如图1所示。该机器人采用独立悬架减振结构进行减振,该减振具有良好的可调节性,其调节机构的三维俯视图如图2所示。该调解机构的工作原理为减振器一端与减振器安装浮动支座通过销钉连接,减振器另一端与车身横架相连,通过调节减振器浮动支座位置,调节减振器预紧力以及减振器与车身横架之间的夹角。在车轮安装架上开两个与其边缘平行且垂直的键槽,由图2可知,减振器安装浮动支座通过螺栓在车轮安装架键槽处相连,通过键槽约束减振器安装浮动支座上下以及前后位置。减振器固定支座通过螺钉与车轮安装架固定连接,减振器浮动支座与减振器固定支座之间通过调整螺杆配合固定,约束减振器浮动支座左右位移。通过调节螺杆来使减振器浮动支座左右滑动,起到调节作用。该调节系统具有结构简单、安装方便以及调节省力的优点。通过该调节系统使整个减振系统具有良好的可调节性,提高了机器人的减振性能,路面适应性大大增加。
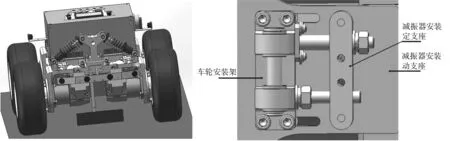
图1 全地形移动机器人结构三维图 图2 调节机构三维俯视图
1.2 四分之一悬架减振系统动力学分析
由于移动机器人车身采用对称结构设计,因此只需研究四分之一移动机器人车身独立悬架减振系统的动力学特性。通过对四分之一移动机器人车身悬架减振系统进行动力学特性研究,推导出其他相同减振机构的动力学特性,简化重复建模过程,提高了研究效率[6]。
通过对减振系统进行简化,绘制力学简图,然后对移动机器人悬架机构进行动力学分析。研究采用拉格朗日方程法建立移动机器人悬架系统动力学方程。四分之一独立悬架减振机构力学简图如图3所示。其中,移动机器人车轮简化为刚度为k1的弹簧;F为地面对车身轮胎的冲击力;k2、C分别为减振器的刚度和阻尼系数;β为减振器与车身定支座的夹角;m1为车轮以及动支座总质量;m2为四分之一车身质量。
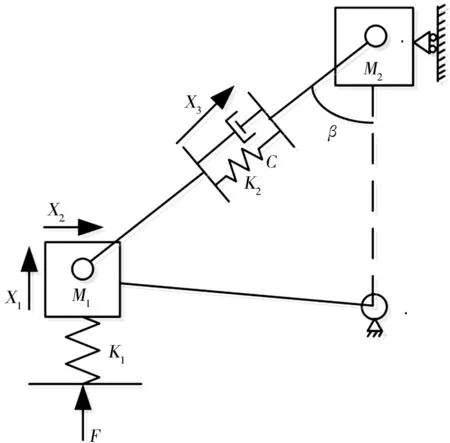
图3 四分之一悬架减振系统力学简图
根据拉格朗日方程法建立四分之一独立悬架减振机构的动力学方程,则建立系统广义坐标为:
(1)
系统的总动能为:
(2)
根据虚功原理可得:
lW=Flx1+[k1x1-(k2x3-cx3)cosβ]lx1+(k2x3-cx3)sinβlx2+(k2x3-cx3)cosβlx3-
m1glx1-m2glx3cosβ,
(3)
系统的广义力为Q,则有:
(4)
(5)
(6)
则可得Q的表达式为:
Q=Cq+Kq+FN,
(7)
(8)
(9)
将式(7)、式(8)、式(9)代入拉格朗日方程中,可得四分之一独立悬架减振机构的动力学方程:
Mq-Cq-Kq-FD=0,
(10)
利用MATLAB软件可以计算出当受到地面冲击时弹簧长度变化情况,由于正弦力比较有代表性,因此结果是在车身受正弦力影响下绘制而成,其正弦力为:
F=100sin(1.5t+30),
(11)
根据弹簧刚度的不同,分别绘制弹簧长度变化量曲线。弹簧刚度为70 N/mm,地面输入信号为正弦信号且作用时间1 s时的弹簧长度变化量如图4所示。弹簧刚度为100 N/mm,其他参数与图4参数相同的弹簧长度变化量如图5所示。通过对比图4、图5发现,在相同地面信号输入时,弹簧刚度越大其峰值越小,当地面输入信号消失时,弹簧长度变化量开始变小;弹簧刚度100 N/mm比70 N/mm时的弹簧长度变化量小,即在相同力的作用下,弹簧刚度越大其变形量越小。
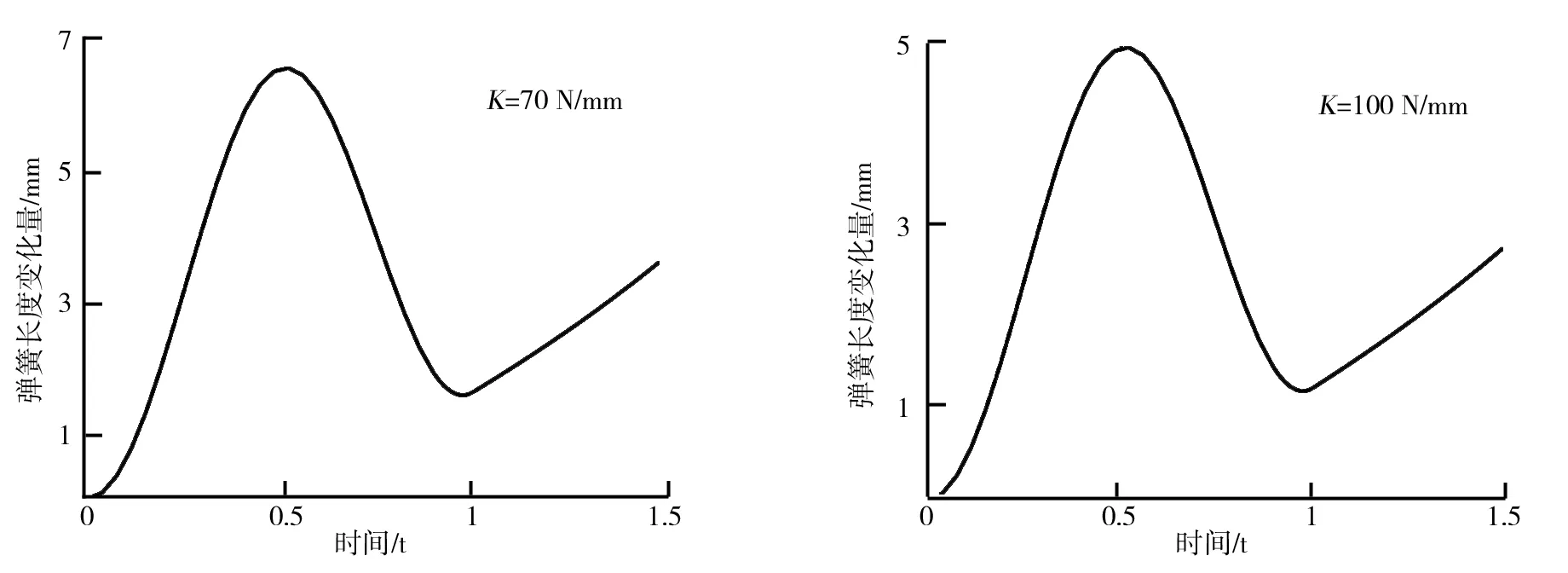
图4 弹簧刚度为70 N/mm时弹簧长度变化量图 图5 弹簧刚度为100 N/mm时弹簧长度变化量图
2 仿真实验分析
利用Adams(Automatic Dynamic Analysis of Mechanical System)软件分析全地形移动机器人独立悬架减振机构动力学特性,配置出合适的减振器参数范围。由于地形不同,车身受地面激励力类型也不同,因此应讨论不同地面激励力对移动机器人减振效果的影响情况[7]。主要讨论的典型激励力有三种情形:第一种是单位阶跃信号力,此种力相当于机器人上下台阶时的受力情况;第二种是斜坡信号力,此种力相当于车轮连续上台阶或下台阶情形;第三种是正弦信号力,此种力相当于移动机器人在坑洼路面运行时的车身受力状态,分别对机器人进行仿真分析,确定出合理的减振器参数范围[8]。
2.1 车身受单位阶跃信号力作用
通过Adams设置一个垂直于轮胎的单向力,单位阶跃信号力设置方法如图6所示。通过step函数进行设置,作用时间为0到1 s内,作用力从300 N变到0 N,模仿上台阶与下台阶时车身受力情形[9]。通过设置不同的弹簧刚度系数进行仿真实验。现设置弹簧刚度的取值范围为70 N/mm左右,取七组弹簧刚度值分别进行仿真,弹簧刚度系数分别为40 N/mm、50 N/mm、60 N/mm、70 N/mm、80 N/mm、90 N/mm、100 N/mm,其中阻尼系数取0.7 Ns/m。测定轮胎离地高度变化图,弹簧长度变化量图以及车身定支座的纵向位移变化图,通过对比分析,确定弹簧刚度值取值范围。其中弹簧阻尼器在Adams的设置如图7所示。通过改变弹簧刚度系数值,分别进行仿真实验,测得实验数据如图8、图9、图10所示。
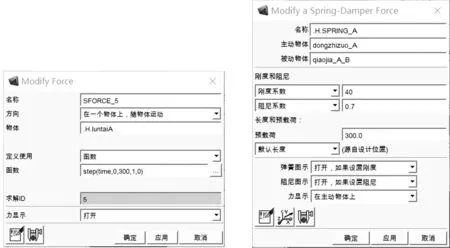
图6 单位阶跃信号力设置 图7 弹簧阻尼器参数图
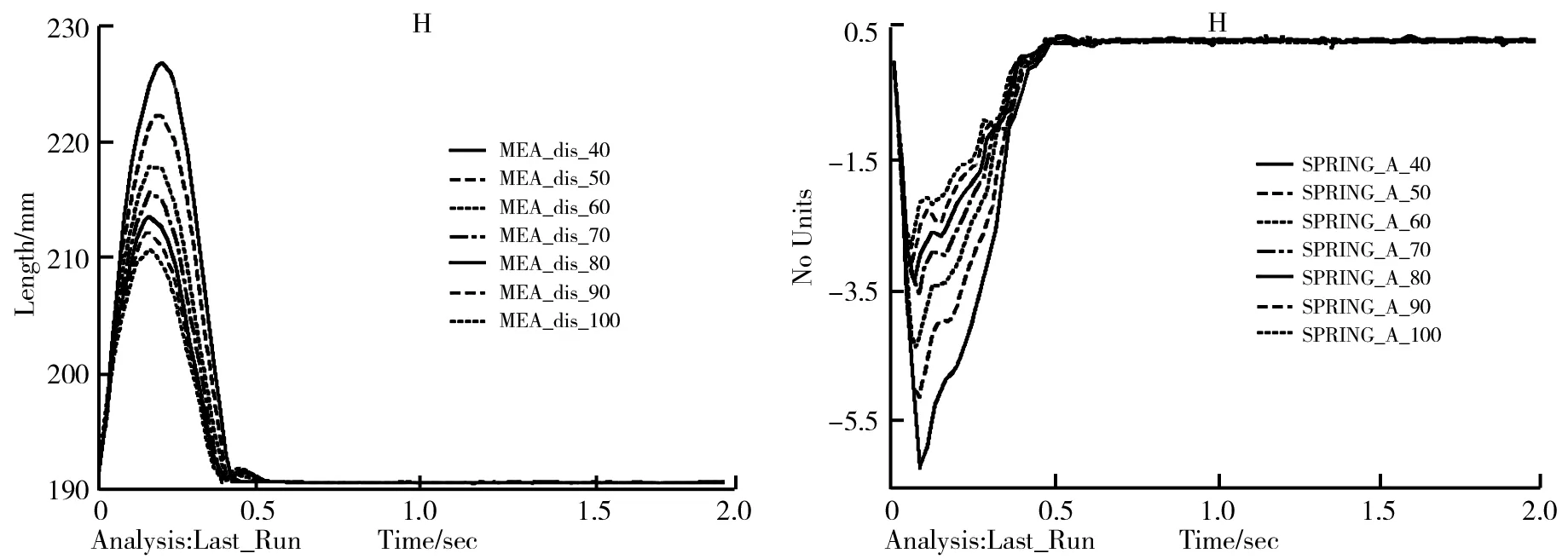
图8 受单位阶跃信号力时车轮纵向位移变化图图9 受单位阶跃信号力时减振器弹簧长度变化量
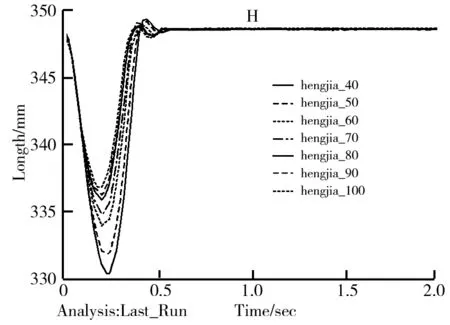
图10 受单位阶跃信号力时车身横架纵向位移图
通过分析图8、图9、图10,整理仿真结果如表1所示。通过表1数据可以发现,当弹簧刚度不断增加时,车轮纵向跳动,弹簧长度变化量以及车轮横架纵向位移均减小,符合前面理论分析计算的结果。对比表上数据发现车轮纵向位移变化量的值远远大于车轮横架纵向位移,而车轮横架纵向位移与车轮纵向位移间差值越大,说明该减振机构的减振效果越好。通过观察表1差值变化情况可知,当弹簧刚度大于70 N/mm时,其前后差值变化量很小,说明当弹簧刚度系数大于70 N/mm时,继续增大弹簧刚度对减振效果的改善不大。因此通过上述分析可知,使用该减振机构的全地形移动机器人具有良好的减振效果,并且弹簧刚度越大其减振效果越好,但当弹簧刚度大于70 N/mm时,增大弹簧刚度其减振效果的改善情况变小,因此弹簧刚度系数范围应大于或等于70 N/mm。
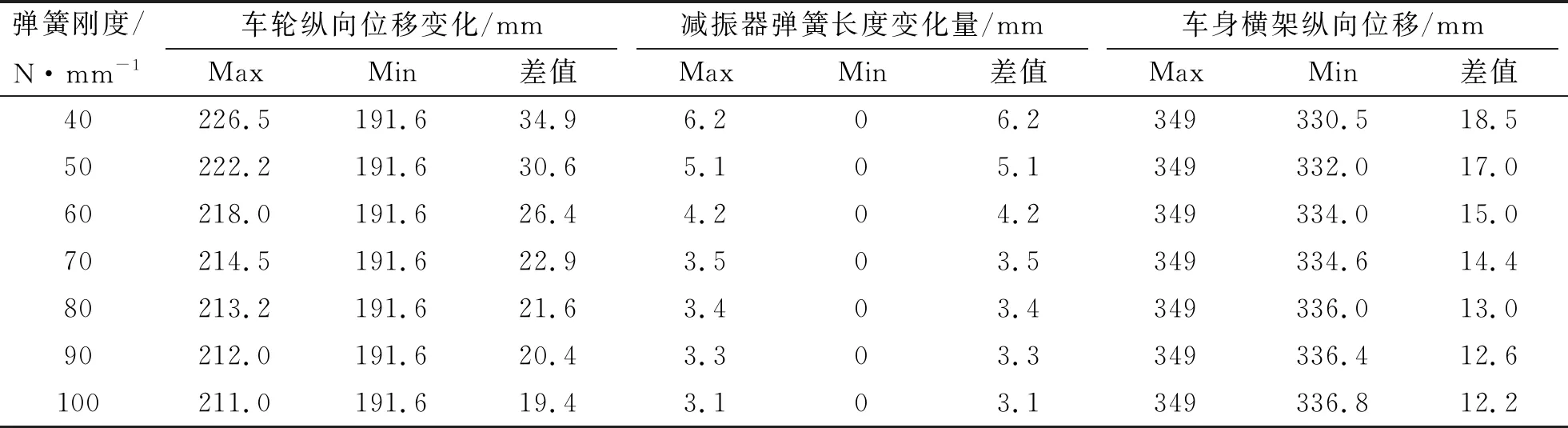
表1 不同刚度弹簧单位阶跃激励响应
2.2 车身受斜坡信号力作用
通过Adams软件设置机器人受地面作用力为斜坡力,地面对轮胎作用力为斜坡力的设置方法如图11所示。该力在仿真过程中的变化情况如图12所示。
图11 斜坡信号力设置 图12 斜坡力变化情况
仿真分析机器人受斜坡力时的动力学特性,其仿真条件设置与受单位阶跃信号力仿真相同。通过仿真分析验证该减振机构在受斜坡力时的减振效果来配置合适的减振器参数,其仿真结果如图13、图14、图15所示。
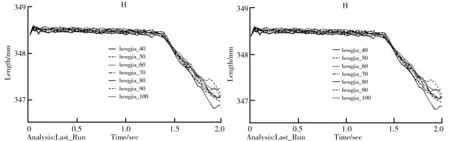
图13 受斜坡力时车身横架纵向位移图 图14 受斜坡力时车轮纵向位移变化图
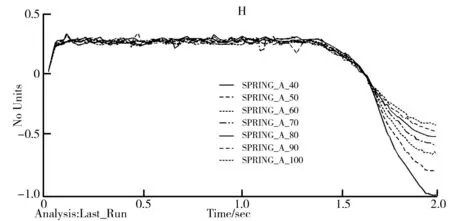
图15 受斜坡力时减振器弹簧长度变化量
通过分析上述仿真结果的变化情况,得到实验数据如表2所示。通过分析表2仿真数据发现,当减振器弹簧刚度不断增加时,悬架减振系统的减振效果越来越好;同时还可以发现,当车身受地面冲击力增加时,车身的振动变得更加剧烈,因此可知,使用该独立悬架减振机构的移动机器人,其机器人在一定地面冲击范围内具有良好的减振效果,因此该移动机器人具有狭义的全地形适用性。
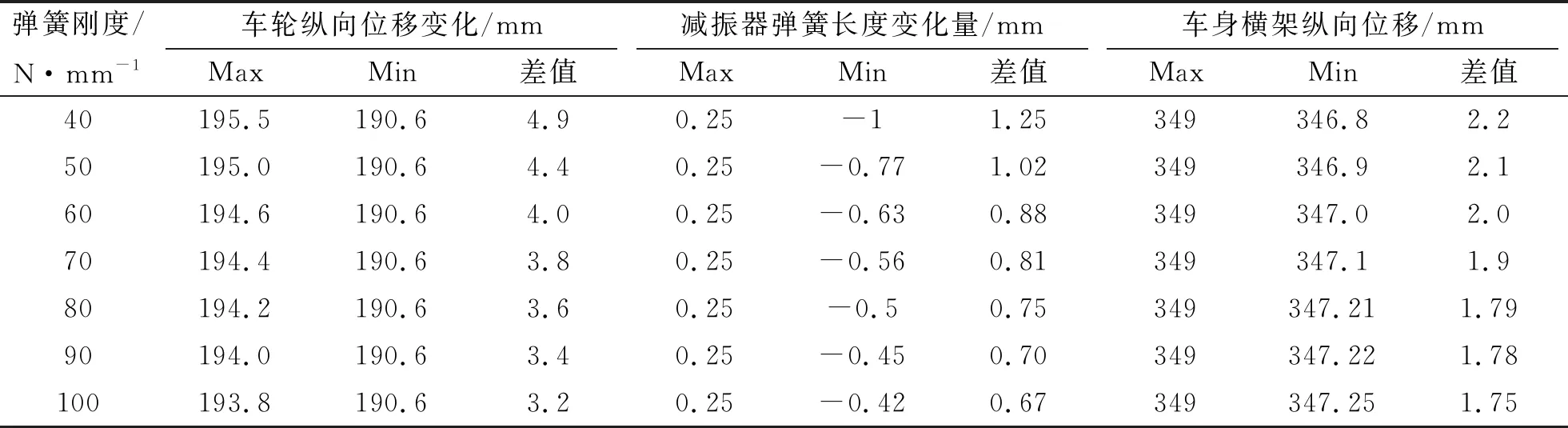
表2 不同刚度弹簧斜坡激励响应
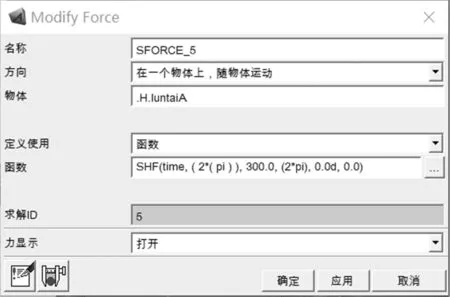
图16 正弦力设置
2.3 机器人受正弦波信号力作用
由于移动机器人在过阶梯型路段时,不管是在上台阶还是下台阶时,其受力方向均为垂直轮胎向上,因此为了更好地模拟实际运行情况,现对机器人所受的正弦力取绝对值,其具体设置如图16所示。通过SHF函数设置正弦力,其正弦力在仿真时的变化情形如图17所示。除了改变车身所受的地面冲击力,其他仿真条件与车身受斜坡力时的仿真条件相同,完成对全地形移动机器人悬架减振机构仿真实验,其仿真结果如图18、图19、图20所示。
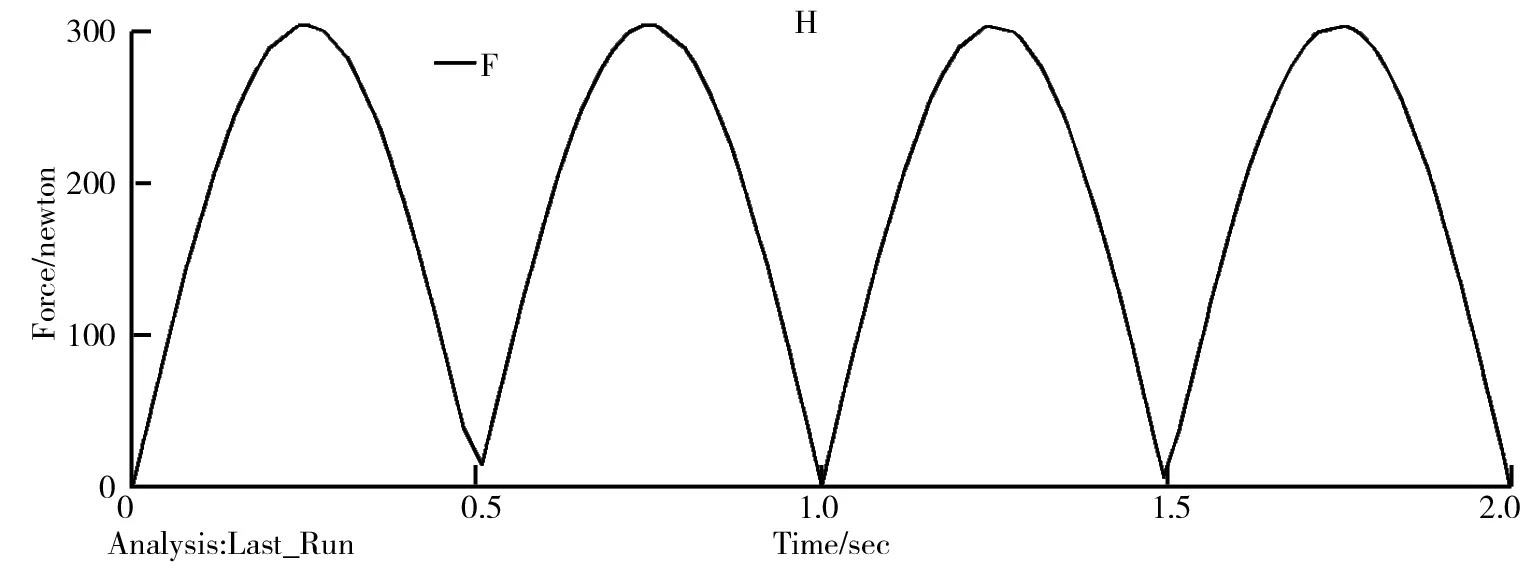
图17 正弦力变化情形图
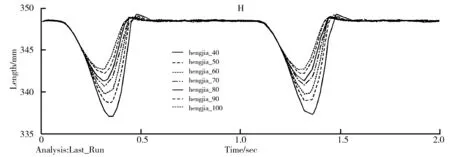
图18 受正弦力时车身横架纵向位移图

图19 受正弦力时减振器弹簧长度变化量
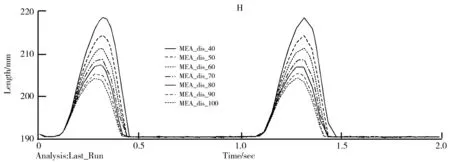
图20 受正弦力时车轮纵向位移变化图
通过对仿真结果进行分析可得,当机器人受地面冲击力为正弦力时,其仿真结果与受单位阶跃信号力的仿真结果相似,其区别在于当系统为正弦力输入时,减振系统的减振数据呈周期性变化。因此可知该机器人悬架减振机构具有良好的减振效果,其弹簧刚度系数应大于 70N/mm。
通过以上三组仿真实验分析可知,当弹簧刚度不断增加时,系统的减振效果逐渐变好,但当弹簧刚度系数大于或等于70 N/mm时,继续增大弹簧刚度系数时,机器人悬架减振机构的减振增强效果逐渐下降。因此通过以上分析现初步确定减振器弹簧刚度系数的取值范围为70 N/mm到90 N/mm之间。
3 结论
研究全地形移动机器人独立悬架减振机构的动态特性,利用拉格朗日方程法完成了四分之一悬架系统的动力学建模,确定了弹簧刚度与悬架减振系统的减振效果之间的变化规律;通过Adams机械系统动力学分析软件完成独立悬架减振机构的动力学仿真实验,机器人独立悬架减振机构减振器弹簧刚度的取值范围应在70 N/mm到90 N/mm之间,此时移动机器人悬架减振系统具有良好的减振效果,满足移动机器人平稳运行的设计目标。

