基于IAHP的电力系统暂态振荡评估

陈 亮，程志友1,*

(1.教育部电能质量工程研究中心，安徽 合肥 230601；2.安徽大学 电子信息工程学院，安徽 合肥 230601)

随着经济的发展与科技的进步，越来越多基于微电子、微处理器等的敏感设备接入电力系统，暂态扰动会对这些敏感设备造成威胁，影响系统的可靠性，对电力系统造成损失[1]。暂态振荡[2]是电压、电流或两者同时存在的稳态条件下的非工频突变，包括正极性值与负极性值。其产生原因有多种，在配电系统中，暂态振荡往往是由变压器的励磁所导致，在电容器的开关过程中，也会发生高幅值与高频率的振荡扰动[3]。振荡扰动事件会造成绝缘击穿、过电压致使半导体器件损坏、短路、数据丢失和破坏系统的稳定性等后果，进一步可能导致设备故障、生产中断、财产损失。当振荡频率接近或者与配电系统及负载的固有频率一致时将形成谐振[4]，引发电气设备受损和大面积停电事故，甚至威胁人身安全。

如今电力系统随着非线性负载的不断引入，系统谐振频率变得越来越低，在某些情况下，谐振频率甚至只有100～150 Hz[5]，低频振荡导致系统谐振的可能性大大增加。因此，对振荡的严重程度评估极其重要。目前，在电能质量扰动的严重程度评估研究中，国内外鲜有对暂态振荡的严重程度评估方法进行研究的，更多关注的是电压暂降与谐波[6]。然而振荡对配电系统同样具有危害性，其严重程度评估也理应受到更多关注。

在现有评估方法中，常被采用的有逼近理想解排序法(Technique for Order Preference by Similarity to an Ideal Solution，TOPSIS)[7]、熵权法[8]、层次分析法(Analytic Hierarchy Process，AHP)[9]等。其中传统层次分析法在20世纪70年代被提出，其具有层次化、结构化的优点，通过对各层次指标之间的重要性进行标度，结合定性分析与定量判断，增强了该方法的科学性与实用性，已被应用于众多领域的评估与决策。暂态振荡中的各指标适用于层次分析法中的层次结构划分，但是传统层次分析法存在最大问题是其不能解决人们理解事物的模糊性，决策者在两两比较中往往带有不确定的主观判断，取一个点值来反映不确定性的判断不够合理。于是多种模糊综合决策方法被提出且广泛使用，如文献[10]采用的模糊层次分析法(Fuzzy Analytic Hierarchy Process，FAHP)，结合了模糊集和层析分析法的概念，利用模糊数解决AHP客观性不足的问题，但其隶属度矩阵通常用隶属度函数确定，目前并没有科学合理的方法确定隶属度函数。文献[11]提出了区间层次分析法(Interval Analytic Hierarchy Process，IAHP)，引用区间数描述不确定性的判断，克服了传统方法的不足。由于振荡评估指标不仅具有不确定性，而且部分指标之间既有联系又相互制约，在应用AHP时各指标间比较标度难以用一个精确的点值表示，同时也为了避免FAHP所存在的问题，研究采用IAHP，通过比较区间数大小进行相对重要程度排序，从而进一步提高评估结果的客观性与科学性。

研究提出的振荡评估方法首先将振荡的多个特征分类为特征因素与系统因素，并建立层次结构，对各个指标进行合理的严重程度分数划分。其次运用IAHP方法的各个步骤获取暂态振荡各指标权重，以便于比较指标间的重要程度。最后将某配电系统产生的振荡作为评估对象，计算该振荡各指标百分制得分，根据总分给出对应的语义评价结果。运用IAHP方法对暂态振荡的严重程度进行评估，克服了传统方法的主观局限性，得到的评估结果具有较高的可信度，具有一定的实际工程意义。

1 振荡严重程度评估方法

1.1 确定评估指标

将基波幅值设为1，暂态振荡的数学模型[12]为：

(1)

式中，τ为时间常数;β为振荡频率系数;ε(t)为阶跃函数;t0表示振荡发生时刻;A表示振荡幅值。根据式(1)，振荡信号外包络可表示为：

(2)

取振荡信号中x轴上方的任意两个峰的顶点坐标(t1,uenvelop(t1)),(t2,uenvelop(t2))，且t2>t1。

(1)根据式(2)计算时间常数τ的值：

(3)

根据式(2)，|uenvelop(t)|的大小随时间按指数逐渐衰减，τ越大，振荡衰减的越慢，反之则越快。当t=4τ时，|uenvelop(t)|衰减到初始值A的1.83%；当t=5τ时，|uenvelop(t)|只有初始值A的0.674%[13]，因此一般取t=(4～5)τ为振荡消失时间，研究取5τ作为振荡的持续时间。

(2)振荡第一个峰的幅值计算：

(4)

(3)能量计算：

(5)

1.2 区间层次分析法

首先分解复杂问题并建立层次结构，再将各指标间两两比较的判断加以量化，建立层次之间的判断矩阵，分别解出判断矩阵权重，最后计算综合权重并排序。

(1)构造区间数判断矩阵。指标间重要程度评判标准如表1所示。采取表1中1～9标度法[14]把各指标两两比较出的相对重要性用区间数表示，形成区间数判断矩阵R。

(6)

rij为区间数判断矩阵R中第i行第j列区间数。

表1指标间重要程度评判标准

rij描述1同样重要3稍微重要5明显重要

(2)区间判断矩阵的一致性检验。在两两比较的过程中，在比较量较多的情况下可能出现判断不一致的情况，如专家认为指标1重要性明显高于指标3，指标2重要性稍微高于指标3，依此推理，指标1重要性应高于指标2，但当专家实际比较指标1和指标2时，可能得出两者重要性相同的判断。这种矛盾的判断结果在比较量较多的情况下更容易出现，因此需要对判断矩阵做一致性检验，采取文献[15]的区间数判断矩阵一致性检验方法，取区间数判断矩阵 ，使用式(7)计算k和m。

(7)

当k≤1且m≥1时，判断矩阵具有较好的一致性；当k>1或者m<1时，则说明判断矩阵的不一致程度超过允许范围，需要重新构建区间判断矩阵，直到通过一致性检验。

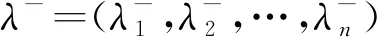
WI=[kλ-,mλ+]=(WI1,WI2,…,WIn),

(8)

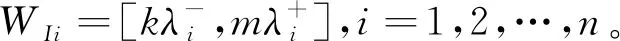
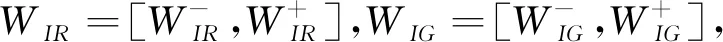
(9)

由于综合权重向量W是由一组区间数组成，会导致评估结果的区间值向两边发散。研究使用可能度排序法[15]将权重值由区间数转化为点值，以便于比较指标的重要性。

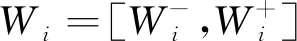
(10)

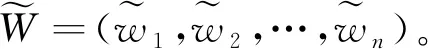
(11)

1.3 振荡评估指标体系

使用区间层次分析法的分层理念建立振荡各评估指标层次关系。暂态振荡综合评估层次结构如图1所示。由图1可知，振荡的持续时间、第一个波峰的峰值、能量作为振荡的特征并归类为特征因素。频率是振荡的另一个重要特征，当振荡频率与系统固有频率的大小接近或一致时可能会造成谐振的后果，振荡频率与固有频率越接近，造成谐振的可能性越大，影响也就越严重。因此，振荡频率也应作为一个评估指标。此外，根据振荡发生的所在系统，考虑到相似的振荡波形在不同电压等级下对电力系统或者设备影响程度也不同，将电压等级这一指标归类为系统因素。

图1 暂态振荡综合评估层次结构

1.4 评分等级划分

(1)各指标评分等级划分。在IEEE制定的电力系统电磁现象的特性参数[17]中，根据频率的大小将暂态振荡分为低频、中频与高频振荡。其中，高频振荡与中频振荡是局部系统对暂态脉冲响应的结果，由于仪器测量范围与精度等原因，这些振荡在实际中很少被观测到。系统中最常见的是低频振荡，文献[18]对低频振荡有详细的综述：低频振荡常发生在公共配电系统和子输电系统中，一般频率在300～900 Hz之间，峰值大小通常是1.3 ～1.5 p.u.，有时可以达到2.0 p.u.，持续时间由系统阻尼大小决定，一般在0.5～3个周期之间。

为了得到直观的评价结果，首先参考电力系统电磁现象的特性参数表与文献[18]对暂态振荡的各特征范围的综述，取振荡持续时间与幅值的最大值，并将其代入振荡模型中计算能量最大值。对这3个评估指标的范围进行等级划分，每个等级都对应一个百分制的分数，根据振荡信号随时间按指数衰减的特点，设s为评分分数，g为等级，可建立如下评分划分方法：

(12)

式中，c为10～15之间的常数。式(12)考虑到了振荡衰减的特点，将这3项指标按该评分方法进行非线性划分，比线性划分更具有合理性。

频率指标评分等级划分应考虑系统谐振频率，设f为振荡频率，f0为系统谐振频率，d为描述振荡频率与系统谐振频率接近程度的系数，则振荡频率评估指标使用以下模型描述：

(13)

根据式(13)，当振荡频率越靠近系统频率，则系数d的值越大，d值的范围为0～1。特征因素的百分制评分等级划分如表2所示。

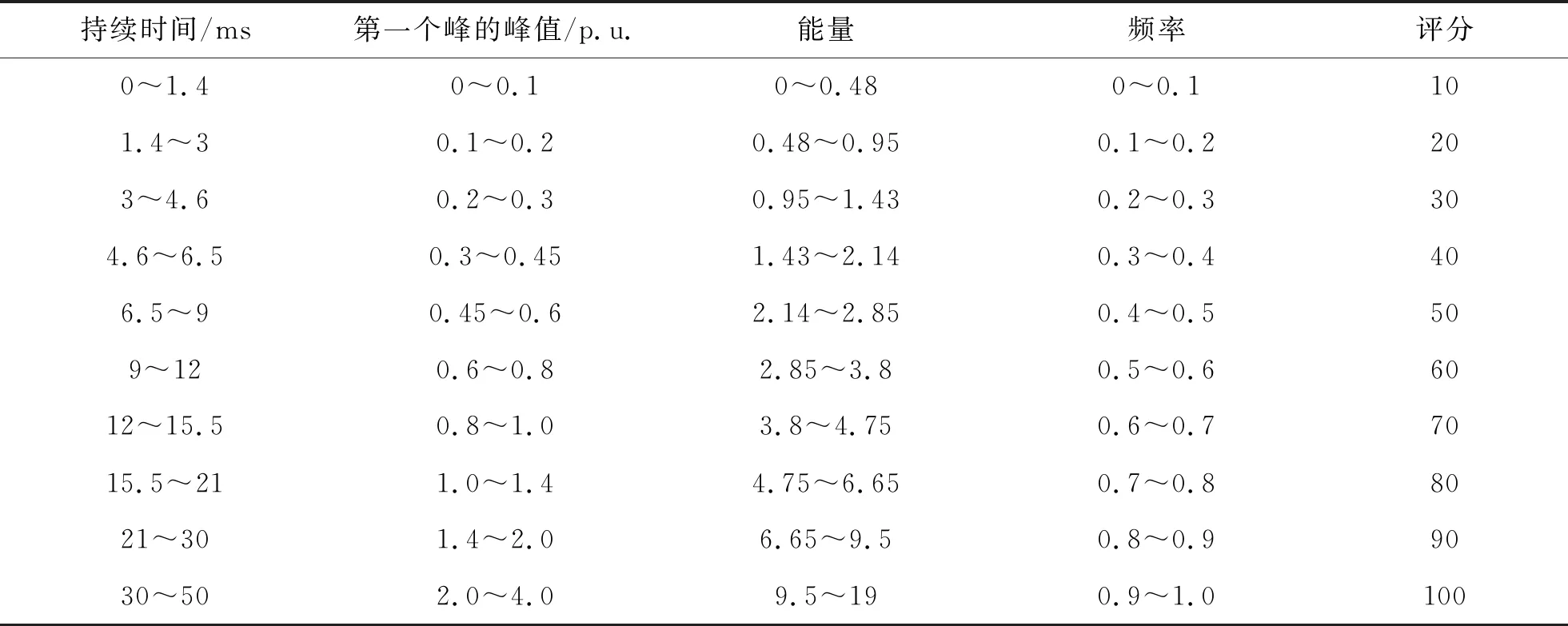
表2 特征因素评分等级

系统因素仅包括电压等级，配电网中高压配电网电压等级为110 kV、66 kV、35 kV，中压为20 kV、10 kV、6 kV，低压为0.4 kV[19]。其百分制划分如表3所示。

表3系统因素评分等级

(2)严重程度等级划分。记各个指标的得分为si，并分别乘以对应的权重，最后求和，求和结果记为h，表示严重程度的评分。计算式如式(14)所示：

(14)

健康指数[20]中严重程度的语义定义与百分制评分对应关系如表4所示，根据严重程度评分h对应严重程度状态得到直观的评价结果。

表4健康指数

严重程度状态健康指数数值h轻微严重0～20较为严重20～40相当严重40～60

2 基于IAHP的振荡评估流程

提出基于IAHP的振荡严重程度评估流程如图2所示。IAHP与传统AHP的基本流程在形式上基本一致，不同之处在于IAHP的判断矩阵由区间数构成，相比于AHP使用点值表示专家的模糊性主观判断，区间数更符合思维与实际情况。利用IAHP的分层理念，结合暂态振荡的特征并考虑产生振荡扰动的系统电压等级，定义目标层、因素层和指标层，构建暂态振荡评估指标体系。通过经AHP改进的IAHP方法获得各区间权重向量，其中一致性检验保证了判断矩阵的合理性，区间数的引用保证了各因素与其所含指标之间判断的模糊性。使用区间可能度排序计算出最终的综合权重向量，解决区间权重引起的评估结果区间扩大的问题。根据综合权重结合各指标得分确定评估对象严重程度的总分和等级。

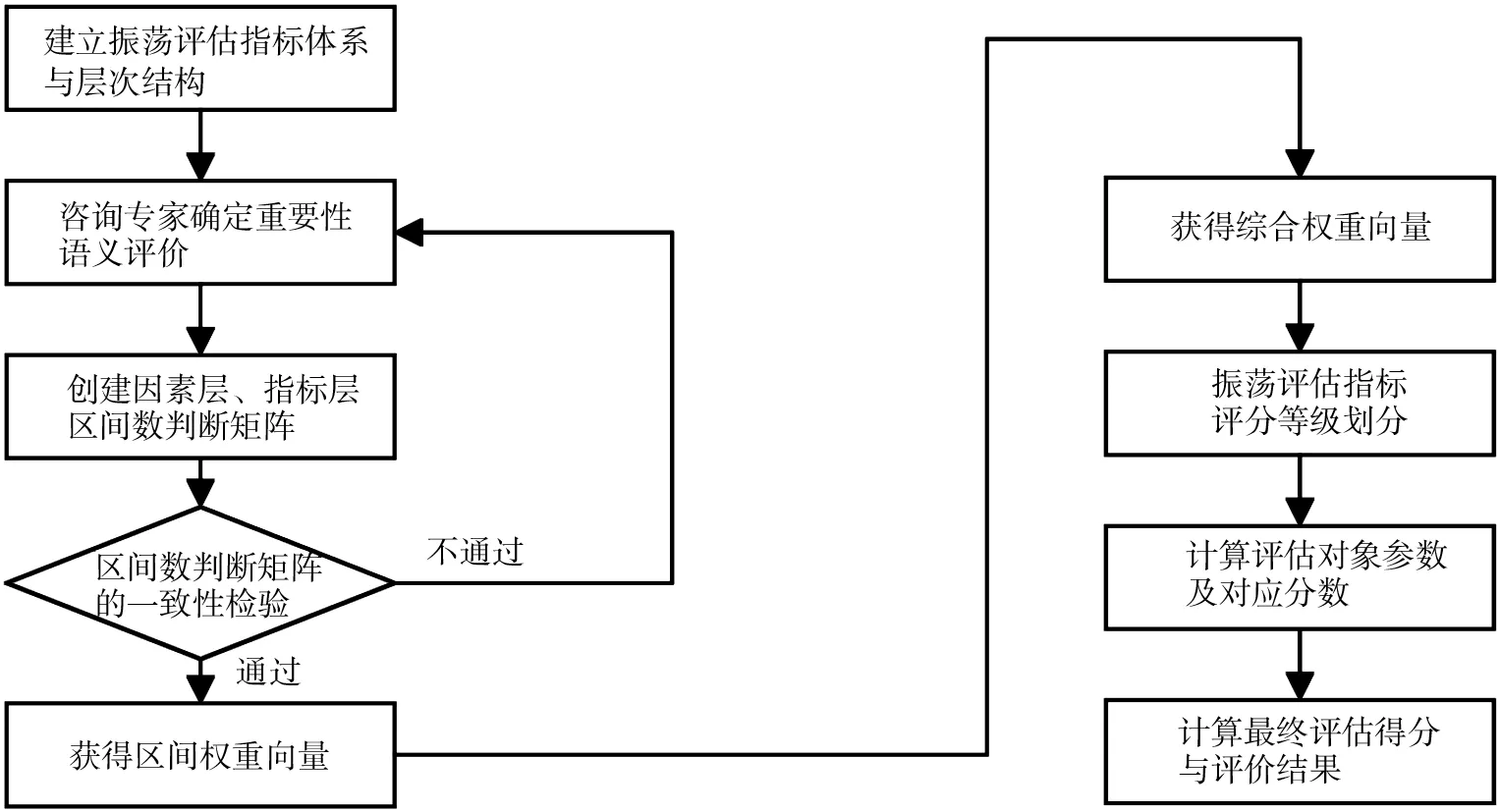
图2 IAHP层次分析评估流程

3 算例分析

以某10kV配电系统中实测暂态振荡扰动事件为评估对象，在该配电系统中，一电容器组投入系统做无功补偿导致暂态振荡产生，已知该系统固有频率约为1 130 Hz。分别运用IAHP与传统AHP两种方法进行评估运算，过程如下。

3.1 评价指标权重的确定

使用IAHP方法构造单层判断矩阵并进行一致性检验，然后利用式(8)计算出区间权重向量，依据文献[9]中AHP方法构造判断矩阵并进行一致性检验，两种方法建立的判断矩阵及求得权重结果分别如表5、表6、表7所示。

表5 总目标判断矩阵与权重

表6 特征因素判断矩阵与权重

表7 系统因素判断矩阵与权重

使用式(9)计算区间综合权重向量，即得WIAHP=(W1,W2,W3,W4,W5)=([0.265 9,0.335 6],[0.137 5,0.195 4],[0.236 6,0.289 3],[0.104 3,0.118 9],[0.164 6，0.174 3])，对区间综合权重WIAHP中各个元素利用式(10)进行两两比较，建立可能度矩阵P如表8所示。

3.2 暂态振荡严重程度评价

该配电系统所产生暂态振荡波形如图3所示。

图3 振荡波形

根据式(3)、式(4)、式(5)计算出各个特征因素指标，所有指标的数值、得分及两种方法求出的各指标权重的统计结果如表9所示。

表9 各指标分值及权重值

使用式(14)计算后得：

根据两种方法取得的综合权重可比较出各指标的重要程度从大到小依次为持续时间、能量、峰值、电压等级、频率。其中，持续时间越长的振荡对系统的冲击时间越长，能量值越大的振荡对系统的冲击程度越大，因此这两个指标的重要性较高。由于该配电系统具有较高的阻抗，增大了振荡的衰减程度，该次振荡在具有较高峰值的情况下持续时间只有约四分之三个周期，能量的数值也较低。从波形看该振荡的第一个峰的峰值较高，而振荡的第一个峰通常最具有破坏性，一个经济有效的办法是电路中短时间接入合闸电阻，可显著抑制电容器投切造成的瞬变。使用复合开关、选相开关等同步合闸断路器实现过零点投切，也可有效减小暂态振荡带来的过电压与通电期间的涌流。

从评估方法方面进行分析，IAHP与AHP计算各指标总分分别为57.783与59.270，对照表4中严重程度评价与得分的对应关系，这两种评价方法的评价结果均显示图3中暂态振荡已经达到了相当严重的水平，各指标权重大小也大抵相当，说明使用传统AHP与IAHP都能很好地体现暂态振荡的严重程度。但从评估过程来看，由于振荡指标之间具有的关联性以及专家的主观性判断，易造成判断结果的不确定性，因此AHP方法在构建由点值构成的判断矩阵时不能体现振荡评估的准确性。IAHP利用区间数能够满足专家对各指标判断的模糊性与不确定性，构建的判断矩阵更客观合理地体现了指标间重要程度，运用IAHP方法的暂态振荡评估结果更加可靠和准确。

4 结论

针对暂态振荡严重程度评价区间性、不确定性的特点，提出基于区间层次分析的暂态振荡严重程度评价方法。与传统层次分析法相比，该方法将区间数应用于各个指标的定量比较中，更能够体现专家判断的模糊性，使评估结果更加合理可信。结果表明，研究所提出的评估方法有效可行，具有一定的实际意义与参考价值。