需求导向的容量设施竞争选址问题研究

俞武扬， 吕 静

(杭州电子科技大学 管理学院，浙江 杭州 310018)

0 引言

经典的设施选址问题通常不需要考虑客户对于所分配设施的意愿，完全从自身的利益或是整体的目标出发为所服务的客户进行设施的定位分派，尤其是一些公共设施(如消防站、邮政服务点、应急避难所等)的选址与定位问题。然而对于一些商业服务类设施(如零售店、加油站、连锁店等)而言，由于需要通过市场竞争而获得客户需求，因此这类设施的选址问题势必要考虑客户对于不同设施属性(如设施规模、所需费用、设施距离等多种因素)的需求意向，通过提供有竞争力的设施选址与设计来获取最大的市场份额及利润，这类选址问题即为竞争设施选址问题[1]。

商业市场弥漫的硝烟使竞争设施选址问题引起了众多学者的关注，Aboolian等[2]从供应商角度出发以最大化利润为目标，在双寡头竞争市场中研究了网络服务供应商的竞争设施选址问题，基于网络选址空间中建立了优化模型并提出了一种精确算法；Godinho等[3]针对互不知情条件下两个决策者同时决策的竞争设施选址问题，构建了纳什均衡模型并提出了求解算法；Ashtiani等[4]在博弈先行者对于跟随者拟建的设施数量未知条件下，研究了Stackelberg博弈框架下的竞争设施鲁棒选址问题。Zhang[5]研究了零售商的竞争设施选址以及同类产品的销售定价问题，以产品的零售价格以及消费者购买产品所需付出的距离成本为关键因素，针对三种不同的选址策略进行了研究。Drezner等[6]假设服务设施在吸引消费者的影响范围内，研究了Stackelberg竞争覆盖选址模型中决策先行者的最优选址策略。Mahmutogullari等[7]对于双寡头Hub竞争设施选址问题进行了研究，通过顺序决策方式以同时确定Hub的选址及相应的服务水平。Fernández等[8]在消费者行为用二元规则以及部分二元规则进行概括的条件下，研究了两种对应的竞争设施选址问题，基于候选点排序思想提出了两种启发式算法。

国内学者针对竞争设施选址问题也进行了一定的研究，杨丰梅等[9]研究了具有聚集效应的竞争设施选址问题，用分枝定界与贪婪算法进行了相应的算法设计；华国伟等[10]分别考虑了市场份额与费用以及企业利润与利润率为双目标的两类竞争设施选址问题，并通过传统的权重分配法转化为单目标模型进行求解；张曦等[11]以市场份额最大化以及企业内部已建设施之间的市场份额吞并最小化为双目标，对于连锁企业竞争设施选址问题进行了研究，设计了求解模型的遗传算法；杨玉香等[12]在多层竞争型闭环供应链环境下，研究了网络设施竞争选址模型，并提出了考虑遗传算法与修正投影算法的混合求解策略；于宏涛等[13]设计了一种混合和声搜索算法以求解竞争设施选址问题；朱华桂等[14]通过定义协同效应函数研究了有协同效应的最大俘获竞争设施选址模型，并对协同效应在竞争设施选址决策过程中所起的作用进行了分析。

目前关于竞争设施选址问题的研究都是基于考虑不同企业如何争夺市场份额的目标上提出的，客户需求仅仅依据距离或吸引力等因素的不同而在设施间进行分配，同时也不考虑设施的容量限制因素。事实上很多情况下客户意愿与设施的容量限制应该是竞争设施选址的两个重要因素，本文在考虑设施的容量限制因素基础上建立了兼顾客户与企业的双目标竞争设施选址模型，通过设计客户意愿与设施服务能力分配机制在竞争设施选址决策中体现了客户的需求导向性。据此提出了求解模型的模拟退火算法，并结合数值例子分析了需求导向服务分配机制、企业预算限额、目标权重系数等重要参数对于选址决策的影响，可以为竞争环境下的企业服务设施选址决策提供有益的参考。

1 数学模型

1.1 问题描述

假设市场上有若干个不同企业所建设的服务设施都可以提供某类产品的销售服务，各个服务设施销售该类产品的价格一致。客户根据自己选择不同设施所需付出购买成本的大小来确定各个设施的优先顺序。企业由于受到服务能力的限制，不一定可以满足所有客户的需求，因此服务设施会按其自身所需付出的服务成本大小对不同的客户需求进行确认。客户与服务设施都在最小化自己付出成本的前提下确定双方的服务定位关系。现在有一个企业A计划在原有设施基础上新增若干个设施，使得企业在设施建设与运营总成本受投资预算约束的条件下最小化所付出总成本，同时也考虑客户所需付出的总成本。对客户与服务设施的互相选择的过程中，由于选择不同设施购买产品服务成本不一因此客户会倾向于优先选择成本低的设施，同时若有多个客户选择同一个服务设施并且总的客户需求超过该设施的服务能力，该设施同样也倾向于选择对提供服务所需付出成本低的客户满足他们的需求。如何在考虑这种互动选择关系的基础上优化企业A的新增设施选址决策？

假设条件：(1)所有客户都根据选择不同服务设施所需付出的成本大小确定设施的优先顺序；(2)所有设施都根据其服务能力以及对不同客户服务时所需付出成本确定是否服务该客户；(3)新建设施的候选点是市场区域中已知的一些离散点；(4)同一客户选择不同服务设施时所需成本与它们之间的距离相关；(5)同一设施对不同客户提供服务时所需付出的成本也与它们之间的距离相关。

1.2 参数和变量设置

I：产品产地的集合；Si：产品产地i的供应能力，i∈I；JO：已建设施集合，其中JA⊂JO表示企业A已建设施集合；JN：新增设施的候选点集合，其中M为候选集合中点的个数；hj：设施j的服务能力，j∈JO∪JN；gj：新增设施j的建设成本，j∈JN；K：客户点集合，用k表示不同的客户；Rk：客户k的产品需求量，k∈K；cjk：设施j为需求点k提供服务所需的单位成本，j∈JO∪JN，k∈K；bjk：需求点k选择设施j为其服务所需付出的单位费用，j∈JO∪JN,k∈K；rij：产地i到设施j的单位服务产品采购价格，i∈I，j∈JO∪JN；G：企业A关于新增设施的建设成本以及服务运营成本的总预算限额；zj：0-1变量，如果在j地新增设施则其值为1，否则其值为0，j∈JN；xij：产地i到服务设施j的产品数量，i∈I，j∈JO∪JN；xjk：设施j到需求点k的产品数量,j∈JO∪JN,k∈K。

1.3 模型建立

(1)

(2)

(3)

(4)

(5)

(6)

zj∈{0,1},j∈JN

(7)

xij≥0,xjk≥0,i∈I,j∈JO∪JN,k∈K

(8)

目标函数f1包括三部分，分别表示企业A的新增设施建设成本、各个设施的产品采购成本、各个设施满足客户需求的服务成本。目标函数f2则表示客户接受企业A旗下设施服务所付出的总成本。约束条件：式(1)表示企业A新增设施建设成本及后续服务成本之和不超过其预算总额；式(2)保证从每个产地采购的产品总量不超过其供应能力；式(3)和(4)分别表示已建设施以及新增设施的产品供应量都不能超过相应设施的服务能力限制；式(5)表示设施服务产品的供应总量不超过从产地采购的服务产品总量；式(6)表示每个客户的需求均被满足；式(7)为新增设施选址变量要求；式(8)为产品数量的非负性要求。

模型中用最小化接受服务所需费用表达客户对于接受不同设施服务的意愿，当有多个客户希望某个设施提供服务而由于设施服务能力限制无法满足所有客户需求时，服务设施再从中选择服务成本最低的若干客户提供服务，这样就形成了先由客户提供意愿再由设施确定服务对象的一种需求导向服务分配机制，仅当设施能够吸引众多客户需求的条件下才有资格选择服务对象，从而体现了企业在竞争设施选址决策中的客户需求导向作用。

2 算法设计

在给定服务设施以及客户需求条件下，客户与设施之间的服务关系由双方的意愿共同确定，可由如下服务分配机制来确定两者对应关系：首先，客户依据当前可选设施所需付出的成本从低到高确定各个设施的优先顺序，按该优先顺序向各个设施提出申请；其次，各设施针对向其提出申请的客户按提供服务所需成本从低到高确定优先顺序，对于该顺序中的每个客户当需求小于当前设施服务能力时则满足该客户需求；最后，对于已满足的客户更新其需求为0，并将当设施的服务能力更新为满足客户需求后所剩余服务能力限制。重复该过程直到满足所有客户的需求或者所有设施的服务能力达到限制。

双目标模型的两个目标需要进行权衡，比较简单的做法是设定权重参数α∈[0,1]，然后定义加权目标函数为fun=αf1+(1-α)f2，基于模拟退火算法框架[14]针对本文研究问题特点设计了求解算法如下：

Step1设置初始值，设定初始温度T0，终止温度Tend，内循环次数L，温度的下降速率q，输入模型的一些已知参数值等。

Step2随机生成初始解z1(0-1向量)来表示选址方案，其中取值为1的候选点表示选为新增设施点，否则不选；利用服务分配机制对市场中的设施与客户进行服务关系分配，在此基础上计算目标函数fun1值；记此时的最优方案为zbest:=z1，且此时的最优目标函数值为fbest:=fun1。

Step3根据当前的初始选址方案z1，随机选择z1中若干位置并将该选址方案在这些位置上的取值进行0-1反转，记反转操作后所得新方案为z2。

Step4同样针对z2利用服务分配机制计算它所对应的目标函数值fun2，计算Δf=exp[-(fun2-fun1)/T]，产生随机数ε∈U(0,1)，若Δf>ε，则令z1:=z2，fun1:=fun2否则保留当前状态不变。

Step5若fbest>fun1，则更新fbest:=fun1,zbest:=z1,并判断内循环变量l是否达到内循环次数L，若否则令l:=l+1转Step3。

Step6更新T:=T·q，若T>Tend则转Step3，否则停止，输出最优目标函数值为fbest，最优选址方案为zbest。

3 算例分析

3.1 案例说明

A公司是一家主营乳制品的农业产业化企业。该公司目前在某地区已建一处分厂，公司的产品由该地区的一家配送中心中转调配后运至各需求点，该配送中心的坐标已知为(46，51)，其处理容量为89000箱。现因业务范围扩大的需要，欲在候选的8个地点新建若干个配送中心以满足业务需求。而在该地区中B公司也有一个配送中心为该地区客户提供配送服务，已知其坐标为(68，53)且处理容量为63000箱，B公司的配送中心与A公司的配送中心之间存在着竞争。该地区的奶制品需求地参数如表1所示。

表1 奶制品需求点需求量及坐标(单位：箱)

奶源产地及新增配送中心候选点参数如表2所示。另外，可以假设各配送中心为需求点提供服务时所需付出的单位成本b以及需求点选择配送中心时的服务成本c与它们之间的距离d线性相关，本算例中假设b=0.9d,c=1.2d。

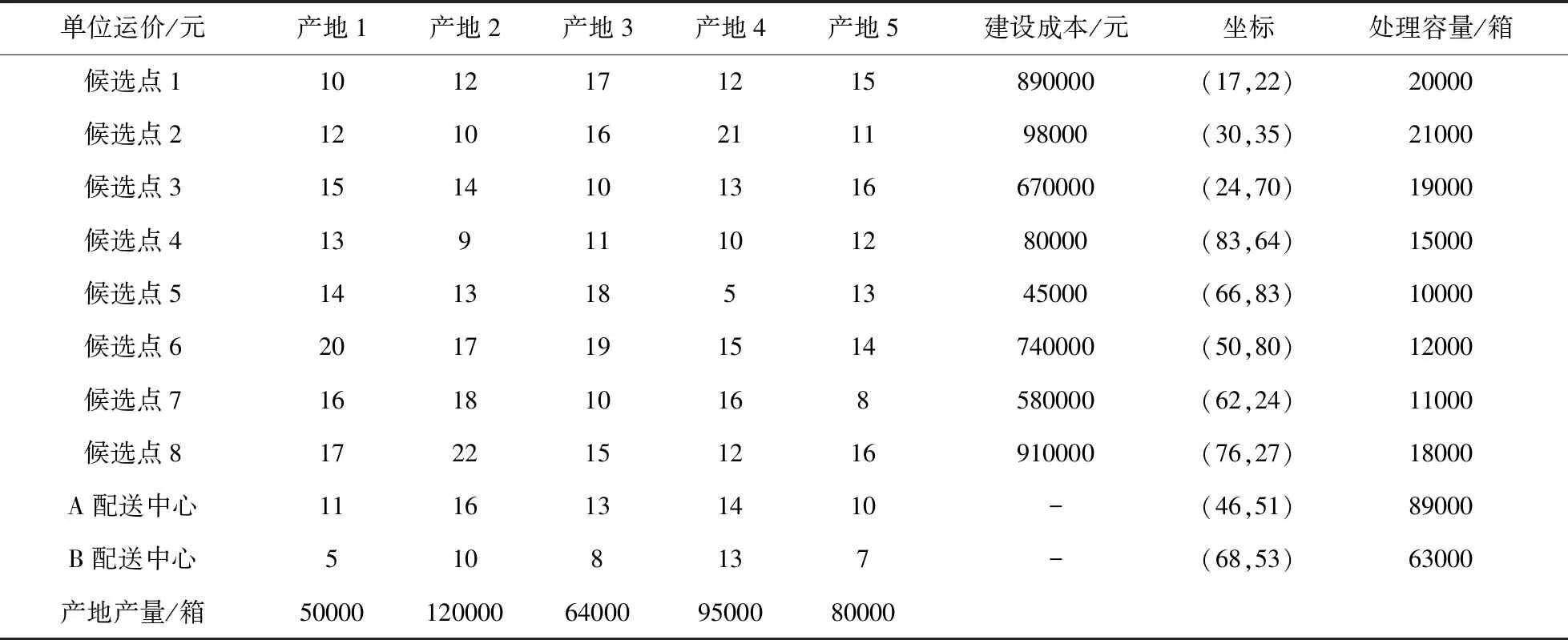
表2 产地及配送中心(包括已建及候选点)相关参数表

根据本文所设计的算法，利用Matlab R2014a软件编程实现算法，硬件运行平台为Dell笔记本电脑，具体配置CPU为Intel i3-3217U 1.6G，4G内存，128G硬盘。算法中的相关参数设置如下：初始温度T0=300，终止温度Tend=1，内循环次数L=10，降温速率q=0.95，在设定目标函数权重系数α=0.5时，对上述问题进行了10次随机计算，每次都得到同样的选址结果即为{0，1，1，0，1，0，0，0}，显示了算法的稳定性(事实上，后面关于所有权重系数的不同取值中，多次计算结果均一致)，10次计算的平均时间为26.6s。

3.2 仿真分析

本文是基于需求导向的竞争设施选址问题研究，客户对于设施的优先意向因素体现了需求导向这一因素，下面首先考虑这一因素在配送中心服务对象方面所产生的影响。

(1)需求导向因素对客户服务关系的影响

不考虑新增配送中心时以及客户的需求意愿条件下，从配送中心成本最小化为目标对各个配送中心所服务的客户进行分配，可得分配方案如图1所示。

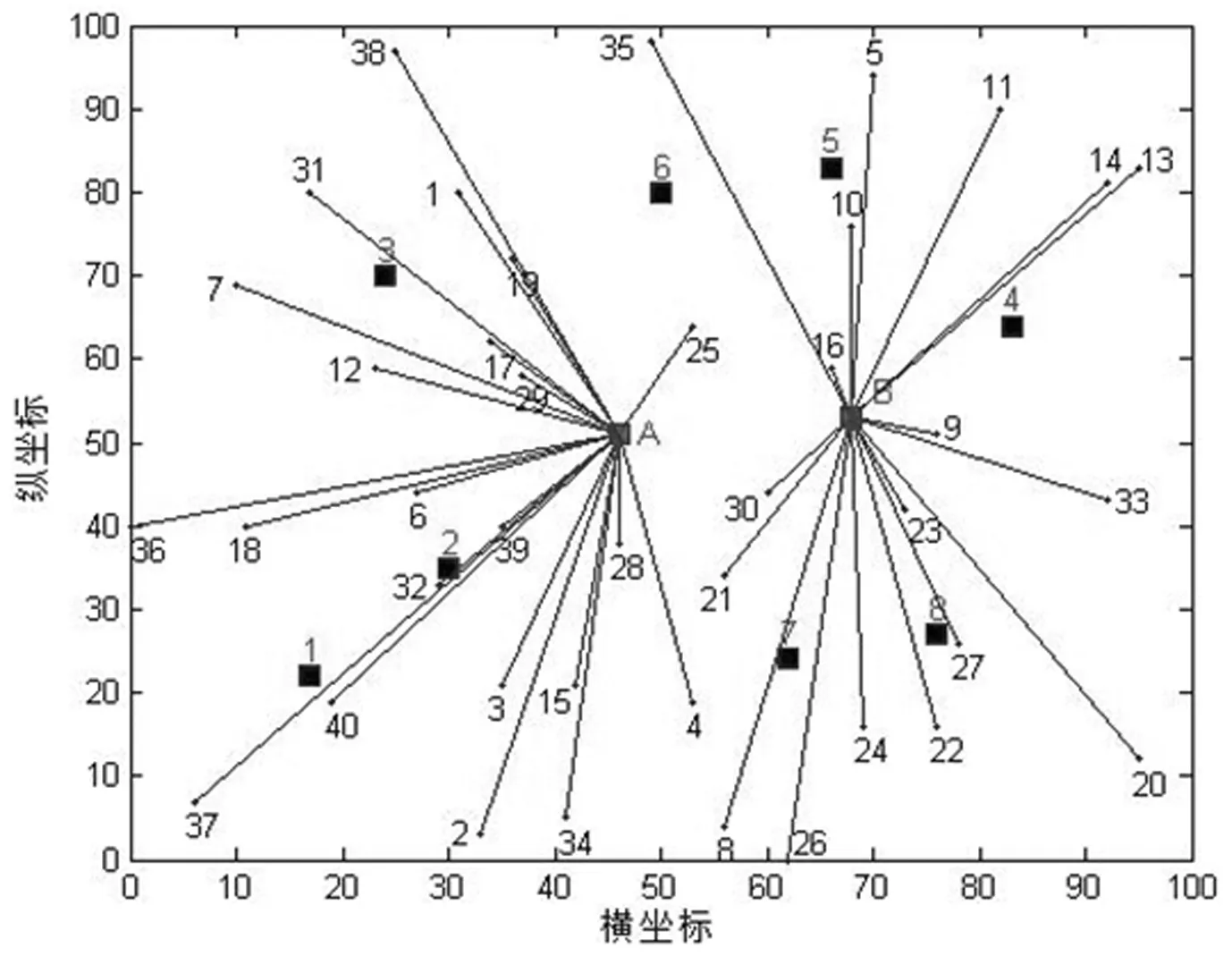
图1 不考虑需求导向因素的分配方案

在这种分配方案中，两个配送中心的运输分配总成本为4190779元，其中企业A与企业B的配送中心总成本分别为2539379元以及1651400元，它们各自所占的市场份额分别为56.4%和43.6%。

若是考虑客户对两个配送中心的优先意向，则由模型与算法可得新的配送服务方案如图2所示。此时A、B两家企业的配送中心总配送成本为4215571元，此时企业A与企业B的配送中心总成本分别为3097514元以及1118057元，它们各自所占的市场份额分别为64.96%和35.04%。

图2 考虑需求导向因素的分配方案

从图1与图2中可以看出，当考虑需求导向因素时客户所需付出的成本相对更低，而相应的配送中心所需付出的成本则会适当增加。

下面进一步分析模型中所涉及的各种参数对企业A新增配送中心的影响。

(2)权重系数对新增配送中心的影响

假设其它所有条件不变，给出权重系数对于新增配送中心方案的影响如表3所示。

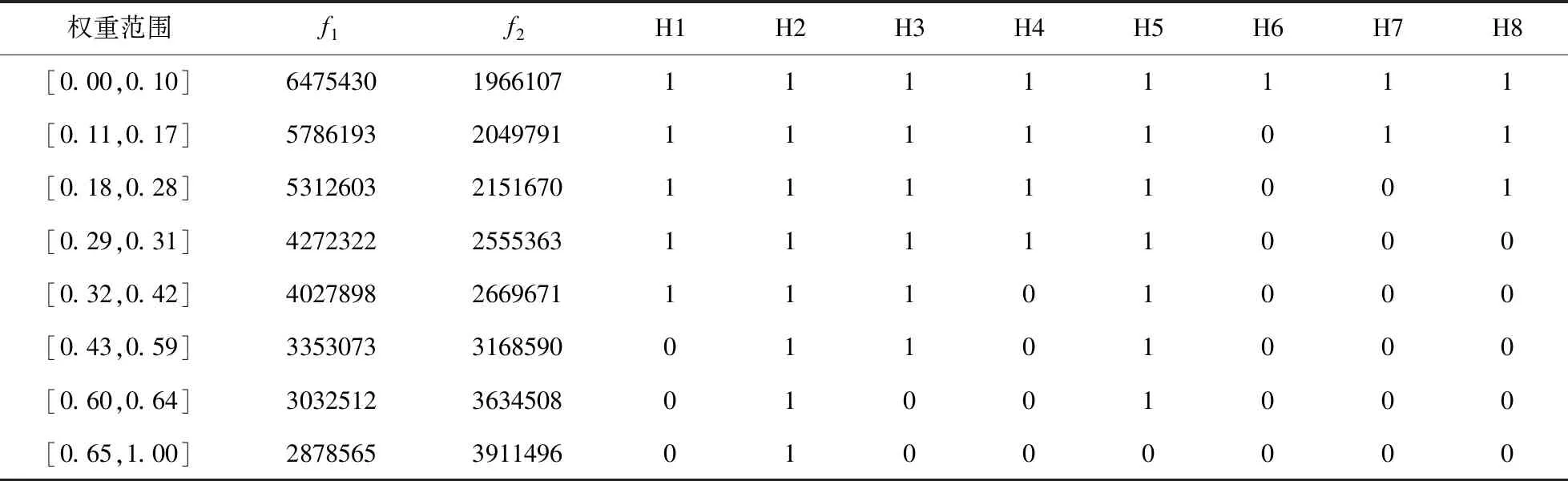
表3 不同权重下企业A新增配送中心的最优选址方案(H1～H8表示配送中心候选点)

由表3可知，不同的权重组合对应着不同的选址方案。随着权重α的增加，企业A新增配送中心的数量逐渐减少，此时企业A所需付出的总成本降低，而客户所需付出的总成本则相应增加。令α从 0 以 0. 01 的步长增加到 1.00，将模型中的两个目标函数值及加权后的目标函数值用图3表示如下。

从图3中可以看出，企业A的总成本随权重α的增大而减小，而客户所需付出的总成本则反之，而加权总成本则随权重α的增大先增后减。

(3)总预算对新增配送中心选址方案的影响

下面研究企业A的总预算对新增配送中心选址方案的影响，取权重参数α分别为0、0.2和0.5，给出企业A的总预算G对于加权总成本的影响情况如图4所示。

图3 各目标函数值随权重的变化图

图4 企业A的总预算额G对加权总成本的影响

由图4可知，给定权重参数值，加权总成本随着企业A总预算额G的增大而下降；而权重参数α的增加意味着企业在考虑新增配送中心时更关心自己付出的成本，因此使得新增配送中心数量下降。下面以权重参数α=0.2为例，详细分析此时所对应的新增配送中心选址方案如图5所示。

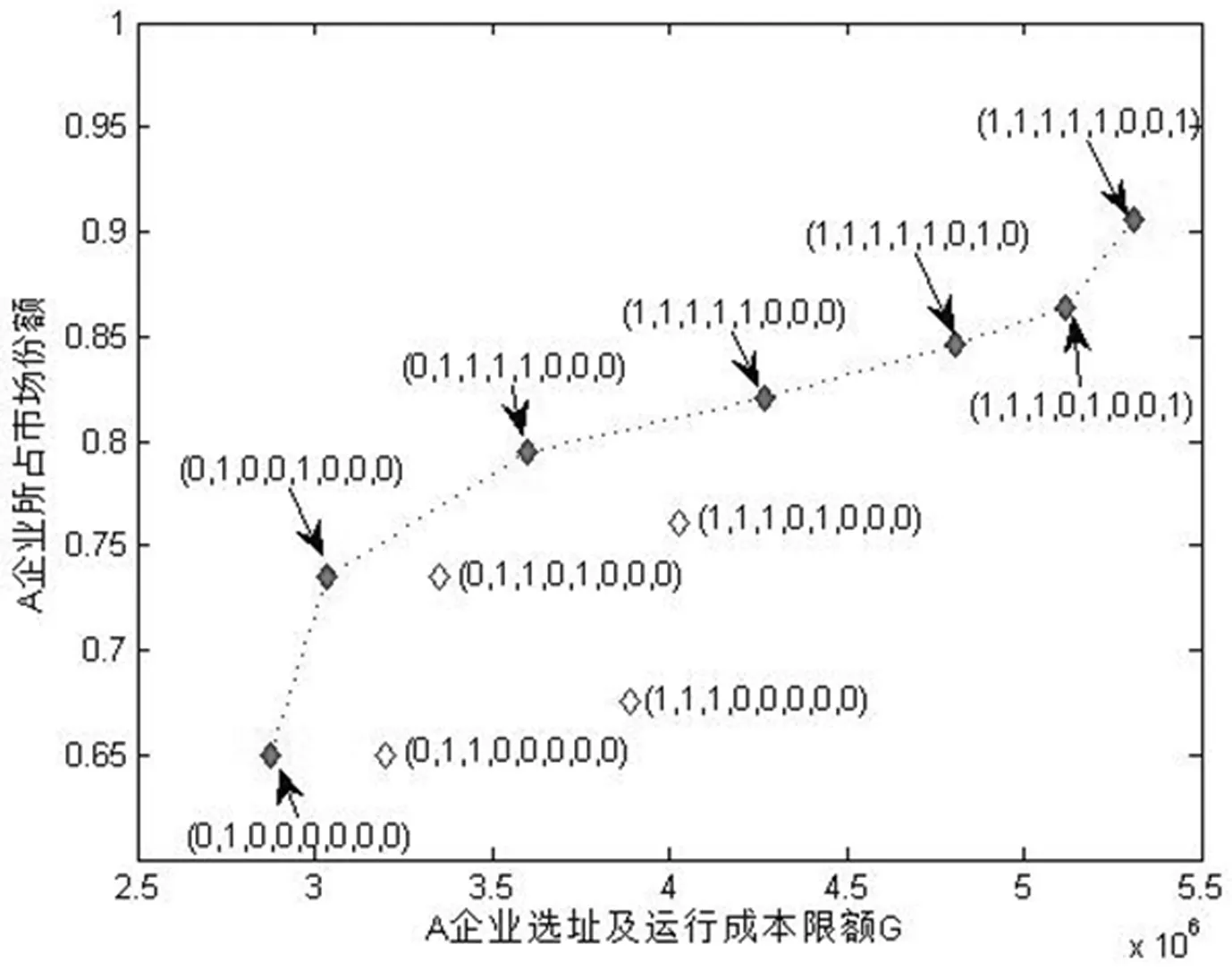
图5 A企业选址与运行预算G对市场份额的影响(α=0.2)

在图5中我们根据选址方案所对应的预算及所占据的市场份额添加了包络线，显然包络线上新增配送中心的选址方案具有更好的投入产出比。按包络线上的选址方案分析可知，A企业的市场份额随着其总预算额G的增加而增加。

(4)参数波动对新增配送中心选址的影响

模型中假设单位运输费用、服务费用及需求量都是已知值，然而这些参数在实际环境中可能会在一定范围内变化，因此有必要研究参数在一定范围内随机波动情况下的选址结果。现令这三个参数在[-10%，+10%]范围内随机波动，令α以0.1为步长从0取到1，以不考虑波动时的原选址方案为标准，每个参数分别在上述范围内取10次随机值，统计该参数取这10个随机值时原最优方案出现的次数，三种参数随机波动后所得结果如表4所示。

表4 参数随机波动情形下的新增配送中心选址稳定性

从表4中可以看出，单位运输成本b的随机波动对于企业A新增配送中心的选址方案影响极小；而客户的单位服务费用c的随机波动对于新增配送中心的选址方案在大多数情况下也影响极小，但在α=0.6时比较特殊5次偏离了原最优选址方案；客户的需求量R对新增配送中心选址方案的影响相对更大，但总体上也仅当α=0.1时稳定性较差。

现设权重参数α从0以0. 1的步长增加到1，给出需求量R随机取值10次所得加权总成本如图6所示。

在图6中可以看出，需求量R的随机波动对加权总成本的影响较为明显，加权总成本随着α的增大呈现先增加后减少的形态。而加权总成本的波动幅度(如图6内小图所示)在α≤0.5的时候相对较小，而在α=0.6时达到最大。

图6 需求量R对目标函数值的影响

4 结语

本文从实际情况出发，以客户的需求为导向来确定服务设施的分配方案，建立了双目标竞争设施选址模型。通过优先考虑客户的需求意愿，设计了一种考虑设施容量限制的服务分配机制，在模拟退火算法框架下设计了基于该分配机制的求解算法。通过数值例子分析了需求导向因素对于设施与客户之间服务方案分配的影响，研究了各种参数对于新增设施选址方案的影响并进行了一定的稳定性分析。后续研究可以进一步从如下方面深入：一是客户选择意愿中另外的影响因素，如设施服务的价格与质量水平；二是考虑企业新增设施可能引发竞争对手的反制措施。

致谢：作者对匿名审稿人为改进本文所提出的建设性意见表示衷心的感谢！